K-th Largest Perfect Subtree Size in Binary Tree

Problem

You are given the root of a binary tree and an integer k.

Return an integer denoting the size of the kth largest __ perfect binary __ subtree, or -1 if it doesn’t exist.

A perfect binary tree is a tree where all leaves are on the same level, and every parent has two children.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12



Input: root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2

Output: 3

Explanation:

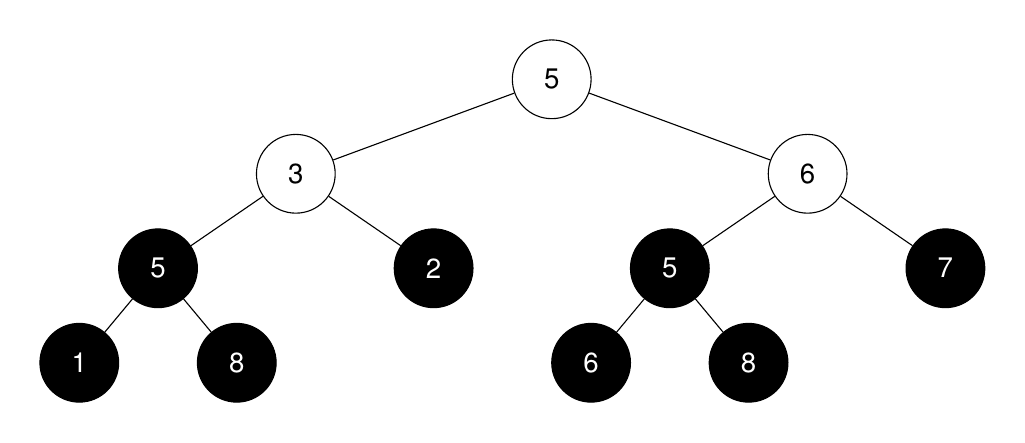
![](https://assets.leetcode.com/uploads/2024/10/14/tmpresl95rp-1.png)

The roots of the perfect binary subtrees are highlighted in black. Their
sizes, in non-increasing order are `[3, 3, 1, 1, 1, 1, 1, 1]`.  
The `2nd` largest size is 3.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11



Input: root = [1,2,3,4,5,6,7], k = 1

Output: 7

Explanation:

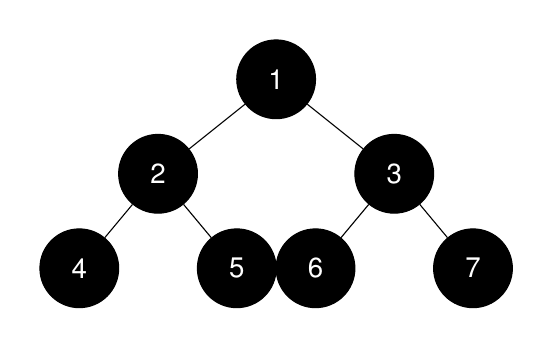
![](https://assets.leetcode.com/uploads/2024/10/14/tmp_s508x9e-1.png)

The sizes of the perfect binary subtrees in non-increasing order are `[7, 3,
3, 1, 1, 1, 1]`. The size of the largest perfect binary subtree is 7.

Example 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11



Input: root = [1,2,3,null,4], k = 3

Output: -1

Explanation:

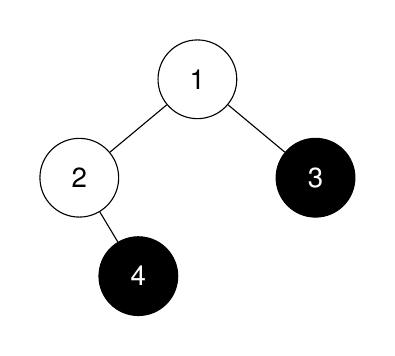
![](https://assets.leetcode.com/uploads/2024/10/14/tmp74xnmpj4-1.png)

The sizes of the perfect binary subtrees in non-increasing order are `[1, 1]`.
There are fewer than 3 perfect binary subtrees.

Constraints

The number of nodes in the tree is in the range [1, 2000].
1 <= Node.val <= 2000
1 <= k <= 10^24

Solution

Method 1 – DFS with Subtree Property Tracking

Intuition

A perfect binary subtree is one where all leaves are at the same level and every parent has two children. We can use DFS to check for this property at every node, collect the sizes, and then sort to find the k-th largest.

Approach

Traverse the tree using DFS.
For each node, recursively get the size and height of left and right subtrees, and whether they are perfect.
A node is the root of a perfect subtree if both children are perfect, and their heights are equal.
If perfect, record the size.
After traversal, sort all sizes in descending order and return the k-th largest, or -1 if not enough.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    int kthLargestSubtreeSize(TreeNode* root, int k) {
        vector<int> sizes;
        function<pair<bool, pair<int,int>>(TreeNode*)> dfs = [&](TreeNode* node) -> pair<bool, pair<int,int>> {
            if (!node) return {true, {0, 0}};
            auto [lp, linfo] = dfs(node->left);
            auto [rp, rinfo] = dfs(node->right);
            bool perfect = lp && rp && linfo.second == rinfo.second;
            int sz = linfo.first + rinfo.first + 1;
            int h = max(linfo.second, rinfo.second) + 1;
            if (perfect) sizes.push_back(sz);
            return {perfect, {sz, h}};
        };
        dfs(root);
        sort(sizes.rbegin(), sizes.rend());
        return k <= sizes.size() ? sizes[k-1] : -1;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func kthLargestSubtreeSize(root *TreeNode, k int) int {
    sizes := []int{}
    var dfs func(*TreeNode) (bool, int, int)
    dfs = func(node *TreeNode) (bool, int, int) {
        if node == nil { return true, 0, 0 }
        lp, lsz, lh := dfs(node.Left)
        rp, rsz, rh := dfs(node.Right)
        perfect := lp && rp && lh == rh
        sz := lsz + rsz + 1
        h := max(lh, rh) + 1
        if perfect { sizes = append(sizes, sz) }
        return perfect, sz, h
    }
    dfs(root)
    sort.Sort(sort.Reverse(sort.IntSlice(sizes)))
    if k <= len(sizes) { return sizes[k-1] }
    return -1
}
func max(a, b int) int { if a > b { return a }; return b }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
    public int kthLargestSubtreeSize(TreeNode root, int k) {
        List<Integer> sizes = new ArrayList<>();
        dfs(root, sizes);
        sizes.sort(Collections.reverseOrder());
        return k <= sizes.size() ? sizes.get(k-1) : -1;
    }
    private int[] dfs(TreeNode node, List<Integer> sizes) {
        if (node == null) return new int[]{1, 0, 0}; // perfect, size, height
        int[] l = dfs(node.left, sizes);
        int[] r = dfs(node.right, sizes);
        boolean perfect = l[0] == 1 && r[0] == 1 && l[2] == r[2];
        int sz = l[1] + r[1] + 1;
        int h = Math.max(l[2], r[2]) + 1;
        if (perfect) sizes.add(sz);
        return new int[]{perfect ? 1 : 0, sz, h};
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
    fun kthLargestSubtreeSize(root: TreeNode?, k: Int): Int {
        val sizes = mutableListOf<Int>()
        fun dfs(node: TreeNode?): Triple<Boolean, Int, Int> {
            if (node == null) return Triple(true, 0, 0)
            val (lp, lsz, lh) = dfs(node.left)
            val (rp, rsz, rh) = dfs(node.right)
            val perfect = lp && rp && lh == rh
            val sz = lsz + rsz + 1
            val h = maxOf(lh, rh) + 1
            if (perfect) sizes.add(sz)
            return Triple(perfect, sz, h)
        }
        dfs(root)
        sizes.sortDescending()
        return if (k <= sizes.size) sizes[k-1] else -1
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution:
    def kthLargestSubtreeSize(self, root: 'TreeNode', k: int) -> int:
        sizes: list[int] = []
        def dfs(node: 'TreeNode') -> tuple[bool, int, int]:
            if not node:
                return True, 0, 0
            lp, lsz, lh = dfs(node.left)
            rp, rsz, rh = dfs(node.right)
            perfect = lp and rp and lh == rh
            sz = lsz + rsz + 1
            h = max(lh, rh) + 1
            if perfect:
                sizes.append(sz)
            return perfect, sz, h
        dfs(root)
        sizes.sort(reverse=True)
        return sizes[k-1] if k <= len(sizes) else -1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


impl Solution {
    pub fn kth_largest_subtree_size(root: Option<Rc<RefCell<TreeNode>>>, k: i32) -> i32 {
        fn dfs(node: Option<&Rc<RefCell<TreeNode>>>, sizes: &mut Vec<i32>) -> (bool, i32, i32) {
            if let Some(n) = node {
                let n = n.borrow();
                let (lp, lsz, lh) = dfs(n.left.as_ref(), sizes);
                let (rp, rsz, rh) = dfs(n.right.as_ref(), sizes);
                let perfect = lp && rp && lh == rh;
                let sz = lsz + rsz + 1;
                let h = lh.max(rh) + 1;
                if perfect { sizes.push(sz); }
                (perfect, sz, h)
            } else {
                (true, 0, 0)
            }
        }
        let mut sizes = vec![];
        dfs(root.as_ref(), &mut sizes);
        sizes.sort_by(|a, b| b.cmp(a));
        if k as usize <= sizes.len() { sizes[(k-1) as usize] } else { -1 }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
    kthLargestSubtreeSize(root: TreeNode | null, k: number): number {
        const sizes: number[] = [];
        function dfs(node: TreeNode | null): [boolean, number, number] {
            if (!node) return [true, 0, 0];
            const [lp, lsz, lh] = dfs(node.left);
            const [rp, rsz, rh] = dfs(node.right);
            const perfect = lp && rp && lh === rh;
            const sz = lsz + rsz + 1;
            const h = Math.max(lh, rh) + 1;
            if (perfect) sizes.push(sz);
            return [perfect, sz, h];
        }
        dfs(root);
        sizes.sort((a, b) => b - a);
        return k <= sizes.length ? sizes[k-1] : -1;
    }
}

Complexity

⏰ Time complexity: O(n log n), where n is the number of nodes. DFS is O(n), sorting sizes is O(m log m) where m ≤ n.
🧺 Space complexity: O(n), for storing subtree sizes and recursion stack.

Problem#

Examples#

Example 1#

Example 2#

Example 3#

Constraints#

Solution#

Method 1 – DFS with Subtree Property Tracking#

Intuition#

Approach#

Code#

Complexity#