Introduction

Typically, multiplying two numbers with n-digits involves n^2 multiplication operations. This is the approach most people use intuitively. Consider the example below for clarity:

1

12 x 15 = ?

It is well known that the result is 180. We can break this calculation into simpler steps. Multiplying 12 × 15 is slightly more complex than 10 × 15, but multiplying by 10 is straightforward since we just append a zero to the number, making 10 × 15 = 150.

To find 12 × 15, we treat it as (10 × 15) + (2 × 15), which simplifies to 150 + 30 = 180.

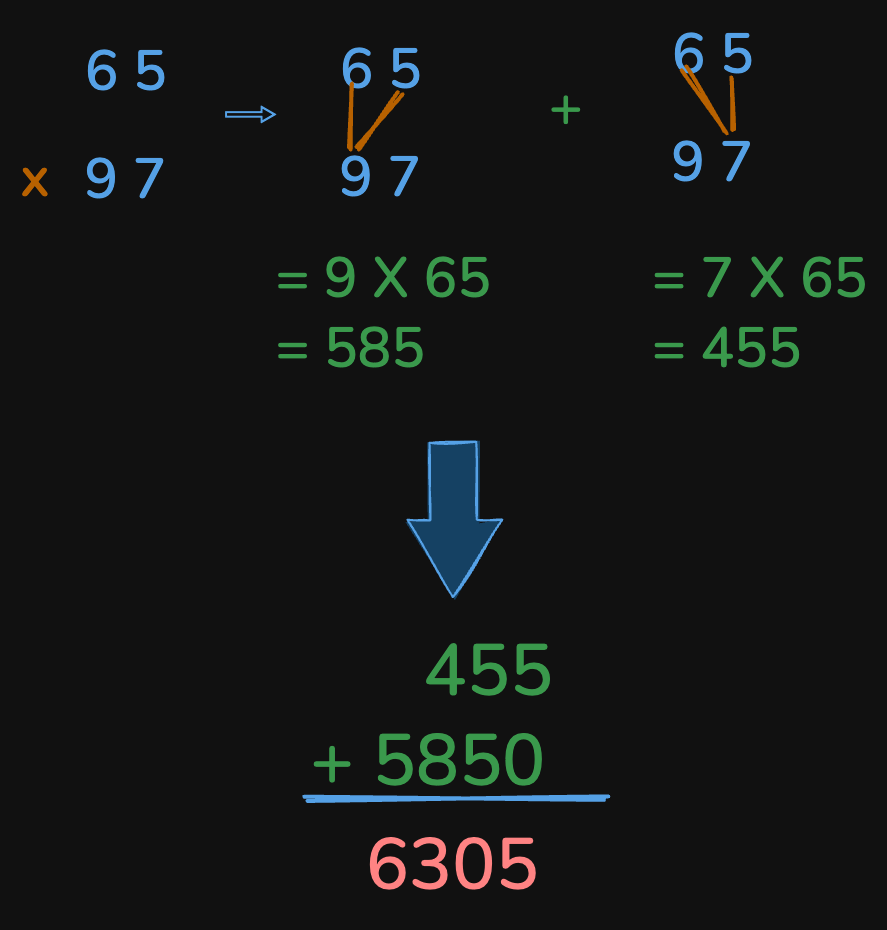
These smaller multiplications and additions make the calculation manageable for small numbers. However, the difficulty increases with larger numbers. For instance, multiplying 65 × 97 requires a more structured approach.

Read more in detail: Multiplication of Two Numbers

Through education, students are introduced to a traditional algorithm that systematically handles such calculations. This method requires four separate multiplications and additional summations for two-digit numbers, as shown diagrammatically below. It becomes inefficient as numbers grow in size, making it laborious for computations like:

1
2
3
4

374773294776321
x
222384759707982

History

In 1960, renowned Russian mathematician Andrey Kolmogorov hypothesised that it was impossible to multiply two n-digit numbers in fewer than n^2 operations. Shortly afterward, a young 23-year-old researcher, Anatolii A. Karatsuba, refuted this claim by introducing a sophisticated divide-and-conquer method to compute products using n^{lg(3)} multiplications—a significant optimisation.

The Algorithm Designer’s Mantra

Algorithm designers live by one core question:

Can this be improved?

This thought becomes particularly important when dealing with straightforward or naive solutions to problems.

The Karatsuba Framework

Karatsuba’s approach efficiently computes the product of two n-digit numbers, x and y, by breaking them into smaller components. Assuming a base B (commonly 10 in the decimal system), we can express the numbers as:

1
2

x = x1 × B^m + x2
y = y1 × B^m + y2

Here:

• x1 and y1 are the higher parts (most significant digits) of the numbers.
• x2 and y2 are the lower parts (least significant digits).
• B^m is the base raised to the power of m, where m is half the number of digits in x or y.

When multiplied, the product xy can be expanded as:

1

xy = (x1 × B^m + x2)(y1 × B^m + y2)

Expanding this results in:

1

xy = (x1 × y1) × B^(2m) + (x1 × y2 + x2 × y1) × B^m + (x2 × y2)

To simplify:

1
2
3

a = x1 × y1 // product of high parts
b = x1 × y2 + x2 × y1 // cross-product of mixed parts
c = x2 × y2 // product of low parts

Combining these results gives:

1

xy = a × B^(2m) + b × B^m + c

While this involves four multiplications, Karatsuba ingeniously reduces it to three by computing b as:

1

b = (x1 + x2)(y1 + y2) - a - c

which we can derive as:

1

b = d - a - c

Finally, combining the results:

1

xy = a × B^(2m) + b × B^m + c

This reduction forms the basis of Karatsuba’s divide-and-conquer approach, which recursively applies the same process to smaller sub-problems, exemplifying the divide-and-conquer paradigm.

Steps

1. • Divide:
     • Split the numbers x and y into x1, x2, y1, and y2 (high and low parts).
   • Recurse:
     • Compute a, c, and d using recursive calls to smaller sub-problems.
   • Combine:
     • Calculate b as d - a - c.
     • Compute the final result using the formula: xy = a × B^(2m) + b × B^m + c

Example Calculation 1

Let’s compute 47 × 78 using Karatsuba’s method:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

x = 47 → (4 × 10 + 7) → x1 = 4, x2 = 7
y = 78 → (7 × 10 + 8) → y1 = 7, y2 = 8

Step 1: Compute partial products
a = (x1 × y1) = (4 × 7) = 28
c = (x2 × y2) = (7 × 8) = 56
b = (x1 + x2) × (y1 + y2) - a - c = (11 × 15) - 28 - 56 = 165 - 84 = 81

Step 2: Combine results
xy = a × 100 + b × 10 + c = (28 × 100) + (81 × 10) + 56 = 4708

Now the thing is that 11 * 15 it’s again a multiplication between 2-digit numbers, but fortunately we can apply the same rules two them. This makes the algorithm of Karatsuba a perfect example of the “divide and conquer” algorithm.

Example Calculation 2

Let’s calculate x = 1234 and y = 5678:

1. Split the numbers:
   • x1 = 12, x2 = 34
   • y1 = 56, y2 = 78
2. Recursive calls:
   • a = karatsuba(12, 56) = 672
   • c = karatsuba(34, 78) = 2652
   • d = karatsuba((12 + 34), (56 + 78)) = karatsuba(46, 134) = 6164
3. Calculate b:
   • b = d - a - c = 6164 - 672 - 2652 = 2840
4. Combine results:
   • xy = a × 10^(2 × 2) + b × 10^2 + c
   • xy = 672 × 10000 + 2840 × 100 + 2652
   • xy = 7006652

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def karatsuba(x, y):
   # Base case: single-digit multiplication
   if x < 10 or y < 10:
      return x * y

   # Determine the size of the numbers
   n = max(len(str(x)), len(str(y)))
   m = n // 2

   # Split the numbers into high and low parts
   x1, x2 = divmod(x, 10**m)
   y1, y2 = divmod(y, 10**m)

   # Recursively calculate a, c, and d
   a = karatsuba(x1, y1)
   c = karatsuba(x2, y2)
   d = karatsuba(x1 + x2, y1 + y2)

   # Compute b using the trick
   b = d - a - c

   # Combine the results
   return a * 10**(2 * m) + b * 10**m + c

Code

C++

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <iostream>
#include <cmath>
#include <string>
using namespace std;

class Solution {
public:
   static long long karatsuba(long long x, long long y) {
      if (x < 10 || y < 10) return x * y;  // Base case

      string xStr = to_string(x), yStr = to_string(y);
      int n = max(xStr.length(), yStr.length());
      int m = n / 2;

      long long high1 = x / pow(10, m);
      long long low1 = x % (long long)(pow(10, m));
      long long high2 = y / pow(10, m);
      long long low2 = y % (long long)(pow(10, m));

      long long a = karatsuba(high1, high2);
      long long c = karatsuba(low1, low2);
      long long b = karatsuba(high1 + low1, high2 + low2) - a - c;

      return a * pow(10, 2 * m) + b * pow(10, m) + c;
   }
};

int main() {
   long long x = 1234, y = 5678;
   cout << "Product: " << Solution::karatsuba(x, y) << endl;
   return 0;
}

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public class Solution {
   public static long karatsuba(long x, long y) {
      if (x < 10 || y < 10) return x * y;  // Base case

      int n = Math.max(String.valueOf(x).length(), String.valueOf(y).length());
      int m = n / 2;

      long high1 = x / (long) Math.pow(10, m);
      long low1 = x % (long) Math.pow(10, m);
      long high2 = y / (long) Math.pow(10, m);
      long low2 = y % (long) Math.pow(10, m);

      long a = karatsuba(high1, high2);
      long c = karatsuba(low1, low2);
      long b = karatsuba(high1 + low1, high2 + low2) - a - c;

      return a * (long) Math.pow(10, 2 * m) + b * (long) Math.pow(10, m) + c;
   }

   public static void main(String[] args) {
      long x = 1234, y = 5678;
      System.out.println("Product: " + karatsuba(x, y));
   }
}

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
   @staticmethod
   def karatsuba(x: int, y: int) -> int:
      if x < 10 or y < 10:  # Base case
            return x * y

      n = max(len(str(x)), len(str(y)))
      m = n // 2

      high1, low1 = divmod(x, 10 ** m)
      high2, low2 = divmod(y, 10 ** m)

      a = Solution.karatsuba(high1, high2)
      c = Solution.karatsuba(low1, low2)
      b = Solution.karatsuba(high1 + low1, high2 + low2) - a - c

      return a * 10 ** (2 * m) + b * 10 ** m + c

# Example
x, y = 1234, 5678
print("Product:", Solution.karatsuba(x, y))

Complexity Analysis

By substituting two multiplications with a single efficient operation, Karatsuba accelerates calculations. The algorithm improves upon the naive O(n^2) complexity, achieving O(n^{lg(3)}) = O(n^1.59). This exponential improvement becomes particularly significant for large inputs, as shown in the graph comparing the two complexities.

Applications

This algorithm is widely used in integer multiplications due to its efficiency. Beyond its use for numbers, the approach is also valuable for polynomial multiplications in computational mathematics.