problemmediumalgorithmsleetcode-582leetcode 582leetcode582

Kill Process

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You have n processes forming a rooted tree structure. You are given two integer arrays pid and ppid, where pid[i] is the ID of the ith process and ppid[i] is the ID of the ith process's parent process.

Each process has only one parent process but may have multiple children processes. Only one process has ppid[i] = 0, which means this process has no parent process (the root of the tree).

When a process is killed , all of its children processes will also be killed.

Given an integer kill representing the ID of a process you want to kill, return a list of the IDs of the processes that will be killed. You may return the answer inany order.

Examples

Example 1:

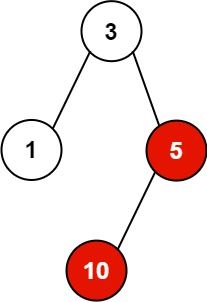
Input: pid = [1,3,10,5], ppid = [3,0,5,3], kill = 5
Output: [5,10]
Explanation:  The processes colored in red are the processes that should be killed.

Example 2:

Input: pid = [1], ppid = [0], kill = 1
Output: [1]

Constraints:

  • n == pid.length
  • n == ppid.length
  • 1 <= n <= 5 * 10^4
  • 1 <= pid[i] <= 5 * 10^4
  • 0 <= ppid[i] <= 5 * 10^4
  • Only one process has no parent.
  • All the values of pid are unique.
  • kill is guaranteed to be in pid.

Solution

Method 1 – Tree Traversal (BFS/DFS)

Intuition

Killing a process means killing all its descendants in the process tree. We can build a parent-to-children mapping and traverse from the kill node to collect all affected processes.

Approach

  1. Build a mapping from parent process id to its children using a hash map.
  2. Start from the process to kill, and traverse (BFS or DFS) to collect all descendants.
  3. Return the list of all killed process ids.

Code

C++
class Solution {
public:
    vector<int> killProcess(vector<int>& pid, vector<int>& ppid, int kill) {
        unordered_map<int, vector<int>> tree;
        for (int i = 0; i < pid.size(); ++i) tree[ppid[i]].push_back(pid[i]);
        vector<int> ans;
        queue<int> q;
        q.push(kill);
        while (!q.empty()) {
            int cur = q.front(); q.pop();
            ans.push_back(cur);
            for (int ch : tree[cur]) q.push(ch);
        }
        return ans;
    }
};
Go
func killProcess(pid []int, ppid []int, kill int) []int {
    tree := map[int][]int{}
    for i, p := range ppid { tree[p] = append(tree[p], pid[i]) }
    ans := []int{}
    q := []int{kill}
    for len(q) > 0 {
        cur := q[0]; q = q[1:]
        ans = append(ans, cur)
        q = append(q, tree[cur]...)
    }
    return ans
}
Java
class Solution {
    public List<Integer> killProcess(List<Integer> pid, List<Integer> ppid, int kill) {
        Map<Integer, List<Integer>> tree = new HashMap<>();
        for (int i = 0; i < pid.size(); ++i)
            tree.computeIfAbsent(ppid.get(i), x -> new ArrayList<>()).add(pid.get(i));
        List<Integer> ans = new ArrayList<>();
        Queue<Integer> q = new LinkedList<>();
        q.offer(kill);
        while (!q.isEmpty()) {
            int cur = q.poll();
            ans.add(cur);
            for (int ch : tree.getOrDefault(cur, List.of())) q.offer(ch);
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun killProcess(pid: List<Int>, ppid: List<Int>, kill: Int): List<Int> {
        val tree = mutableMapOf<Int, MutableList<Int>>()
        for (i in pid.indices) tree.getOrPut(ppid[i]) { mutableListOf() }.add(pid[i])
        val ans = mutableListOf<Int>()
        val q = ArrayDeque<Int>()
        q.add(kill)
        while (q.isNotEmpty()) {
            val cur = q.removeFirst()
            ans.add(cur)
            tree[cur]?.forEach { q.add(it) }
        }
        return ans
    }
}
Python
class Solution:
    def killProcess(self, pid: list[int], ppid: list[int], kill: int) -> list[int]:
        from collections import defaultdict, deque
        tree: dict[int, list[int]] = defaultdict(list)
        for c, p in zip(pid, ppid):
            tree[p].append(c)
        ans: list[int] = []
        q = deque([kill])
        while q:
            cur = q.popleft()
            ans.append(cur)
            q.extend(tree[cur])
        return ans
Rust
use std::collections::{HashMap, VecDeque};
impl Solution {
    pub fn kill_process(pid: Vec<i32>, ppid: Vec<i32>, kill: i32) -> Vec<i32> {
        let mut tree = HashMap::new();
        for (&c, &p) in pid.iter().zip(ppid.iter()) {
            tree.entry(p).or_insert(vec![]).push(c);
        }
        let mut ans = vec![];
        let mut q = VecDeque::new();
        q.push_back(kill);
        while let Some(cur) = q.pop_front() {
            ans.push(cur);
            if let Some(children) = tree.get(&cur) {
                for &ch in children { q.push_back(ch); }
            }
        }
        ans
    }
}
TypeScript
class Solution {
    killProcess(pid: number[], ppid: number[], kill: number): number[] {
        const tree = new Map<number, number[]>();
        for (let i = 0; i < pid.length; ++i) {
            if (!tree.has(ppid[i])) tree.set(ppid[i], []);
            tree.get(ppid[i])!.push(pid[i]);
        }
        const ans: number[] = [];
        const q: number[] = [kill];
        while (q.length) {
            const cur = q.shift()!;
            ans.push(cur);
            if (tree.has(cur)) q.push(...tree.get(cur)!);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of processes. Each process is visited once.
  • 🧺 Space complexity: O(n), for the tree mapping and queue.

Comments