Knight Dialer

Problem

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

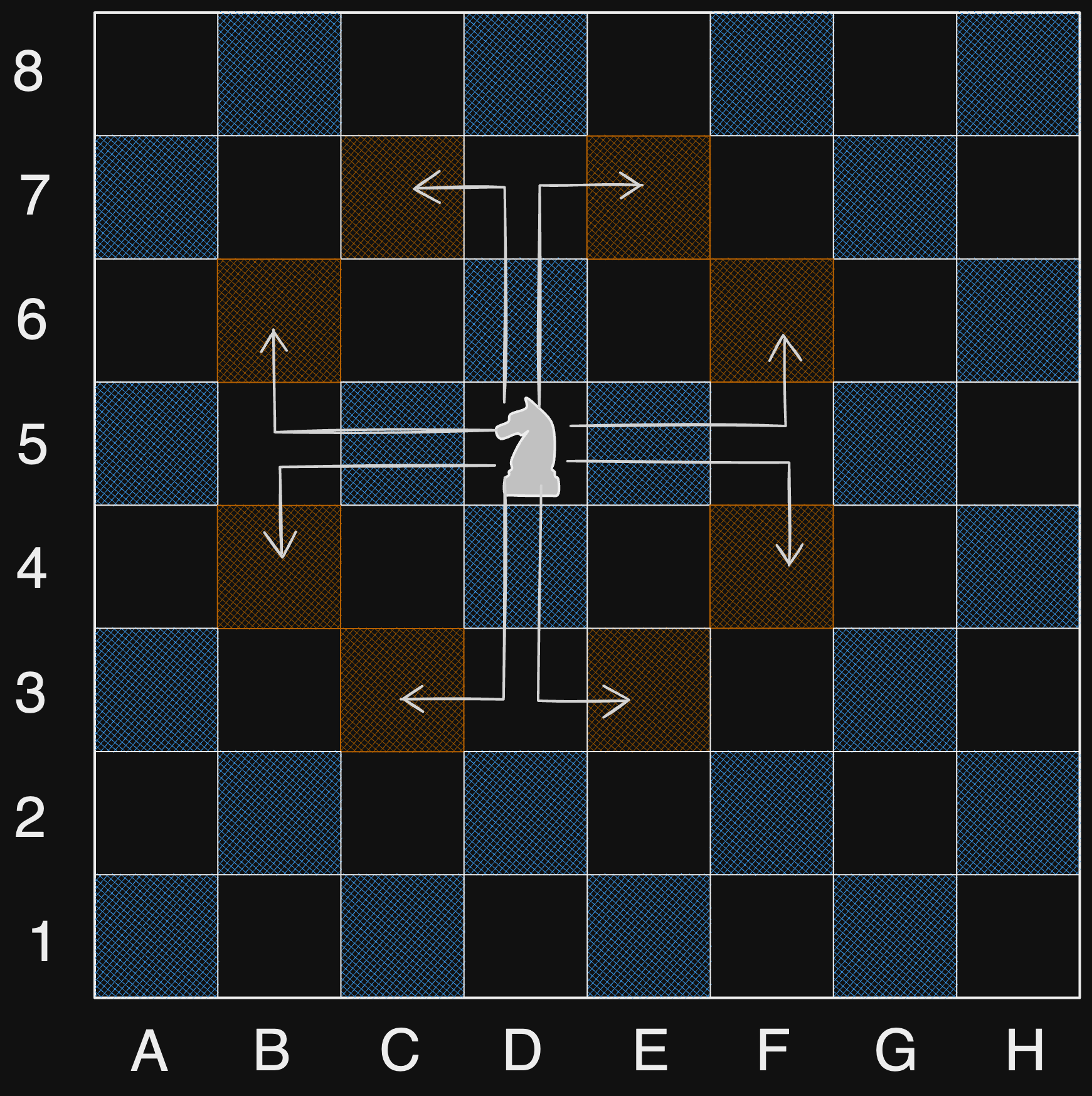
knights-move-chess.excalidraw

We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

$$ \begin{bmatrix} \colorbox{blue} 1 & \colorbox{blue} 2 & \colorbox{blue} 3 \\ \colorbox{blue} 4 & \colorbox{blue} 5 & \colorbox{blue} 6 \\ \colorbox{blue} 7 & \colorbox{blue} 8 & \colorbox{blue} 9 \\ \colorbox{red} * & \colorbox{blue} 0 & \colorbox{red} \# \end{bmatrix} $$

Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 10^9 + 7.

Examples

Example 1:

1
2
3


Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

1
2
3


Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

1
2
3


Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Solution

Method 1 - Recursion

The knight can only stand on numeric keys (blue cells), and it moves in an “L” shape, which means:

Two squares in one direction and one square perpendicular, or
One square in one direction and two squares perpendicular.

Based on that we can we define moves[] matrix. Then for each element moves[i] we get following knight moves:

from 0 we can either go to cells 4 or 6. Hence moves[0] = [4, 6]
from 1 we can either go to cells 6 or 8. Hence moves[1] = [6, 8]

So, this is how we can define our moves:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


moves = [
	[4, 6],     # 0 
	[6, 8],     # 1 
	[7, 9],     # 2 
	[4, 8],     # 3 
	[3, 9, 0],  # 4 
	[],         # 5 (not used)
	[1, 7, 0],  # 6 
	[2, 6],     # 7 
	[1, 3],     # 8 
	[2, 4]      # 9 
]

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


class Solution {

	private static final int[][] MOVES = {
		{4, 6},     // 0 
		{6, 8},     // 1 
		{7, 9},     // 2 
		{4, 8},     // 3 
		{3, 9, 0},  // 4 
		{},         // 5 (not used)
		{1, 7, 0},  // 6 
		{2, 6},     // 7 
		{1, 3},     // 8 
		{2, 4}      // 9 
	};
 

	private static final int MOD = 1000000007;

	public int knightDialer(int n) {
		int result = 0;

		for (int i = 0; i <= 9; i++) {
			result = (result + knightDialerFrom(i, n)) % MOD;
		}

		return result;
	}

	private int knightDialerFrom(int current, int n) {
		if (n == 1) return 1;

		int total = 0;

		for (int next: MOVES[current]) {
			total = (total + knightDialerFrom(next, n - 1)) % MOD;
		}

		return total;
	}
}

Complexity

⏰ Time complexity: O(9^n)
- For each digit, the knight can make up to 2 or 3 jumps based on the moves array.
- Let f(n, d) be the number of ways to reach a number of length n starting at digit d.
- Without memoization, the total number of calls can be very large as it forms a tree-like structure.
- In general, for n moves, the number of recursive calls can be approximated by O(9^n) in the worst case, because of the overlapping subproblems and exponential growth in recursive calls.
🧺 Space complexity: O(n), assuming recursion stack

Method 2 - Top Down DP with memo

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


class Solution {

	private static final int[][] MOVES = {
		{4, 6},     // 0 
		{6, 8},     // 1 
		{7, 9},     // 2 
		{4, 8},     // 3 
		{3, 9, 0},  // 4 
		{},         // 5 (not used)
		{1, 7, 0},  // 6 
		{2, 6},     // 7 
		{1, 3},     // 8 
		{2, 4}      // 9 
	};
	
	private static final int MOD = 1000000007;

	private int[][] memo;

	public int knightDialer(int n) {
		memo = new int[n + 1][10];

		for (int[] row: memo) {
			Arrays.fill(row, -1);
		}

		int result = 0;

		for (int i = 0; i <= 9; i++) {
			result = (result + knightDialerFrom(i, n)) % MOD;
		}

		return result;
	}

	private int knightDialerFrom(int current, int n) {
		if (n == 1) return 1;

		if (memo[n][current] != -1) return memo[n][current];

		int total = 0;

		for (int next: MOVES[current]) {
			total = (total + knightDialerFrom(next, n - 1)) % MOD;
		}

		memo[n][current] = total;
		return total;
	}

}

Complexity

⏰ Time complexity: O(n)
- Each state (n, d) is computed at most once and stored in memo.
- There are 10*n possible states.
- For each state (n, d), we iterate over a constant list of knight moves (at most 3 moves). So, we get O(10*n) = O(n)
🧺 Space complexity: O(n)
- The memoization table, which stores results for all states (n, d), which takes O(10n)
- The recursion stack depth, which is n.

Method 3 - Bottom up DP

The idea is to track the number of ways to reach each numeric cell on the phone pad with a certain number of moves, leveraging the unique movement capabilities of a chess knight.

Here are the steps we can take:

Initialization:
- Create a DP table where dp[i][j] represents the number of ways to reach cell j with i moves.
- Initialize the base cases where dp[0][j] = 1 for all numeric keys j (since there is 1 way to be on a key initially without any moves).
Valid Moves:
- Define the possible knight moves from each numeric cell. These are the valid transitions based on knight’s movement rules.
DP Transition:
- Update the DP table based on possible moves. For each move count i, update dp[i+1] (next move count) based on current move count dp[i] using the valid knight moves.
Result Calculation:
- Sum the number of ways to end up on any numeric key after n-1 moves (since another move is required to reach a phone number of length n).
Modulo Operation:
- Since the result can be large, take the result modulo (10^9 + 7).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


class Solution {

	private static final int[][] MOVES = {
		{4, 6},     // 0 
		{6, 8},     // 1 
		{7, 9},     // 2 
		{4, 8},     // 3 
		{3, 9, 0},  // 4 
		{},         // 5 (not used)
		{1, 7, 0},  // 6 
		{2, 6},     // 7 
		{1, 3},     // 8 
		{2, 4}      // 9 
	};
	
	private static final int MOD = 1000000007;
	
	public int knightDialer(int n) {
		// Initialize DP table
		int[][] dp = new int[n + 1][10];

		// Base case: 1 way to dial a number with length 1 (initial position)
		for (int i = 0; i <= 9; i++) {
			dp[1][i] = 1;
		}

		// Fill DP table
		for (int i = 1; i < n; i++) {
			for (int j = 0; j <= 9; j++) {
				if (dp[i][j] > 0) {
					for (int next: moves[j]) {
						dp[i + 1][next] = (dp[i + 1][next] + dp[i][j]) % MOD;
					}
				}
			}
		}

		// Sum all ways to dial a number of length n
		long result = 0;

		for (int i = 0; i <= 9; i++) {
			result = (result + dp[n][i]) % MOD;
		}

		return (int) result;
	}

}

Complexity

⏰ Time complexity: O(n)
🧺 Space complexity: O(n)

Problem#

Examples#

Solution#

Method 1 - Recursion#

Code#

Complexity#

Method 2 - Top Down DP with memo#

Code#

Complexity#

Method 3 - Bottom up DP#

Code#

Complexity#

Problem

Examples

Solution

Method 1 - Recursion

Code

Complexity

Method 2 - Top Down DP with memo

Code

Complexity

Method 3 - Bottom up DP

Code

Complexity