Problem

On an n x n chessboard, a knight starts at the cell (row, column) and attempts to make exactly k moves. The rows and columns are 0-indexed, so the top-left cell is (0, 0), and the bottom-right cell is (n - 1, n - 1).

A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.

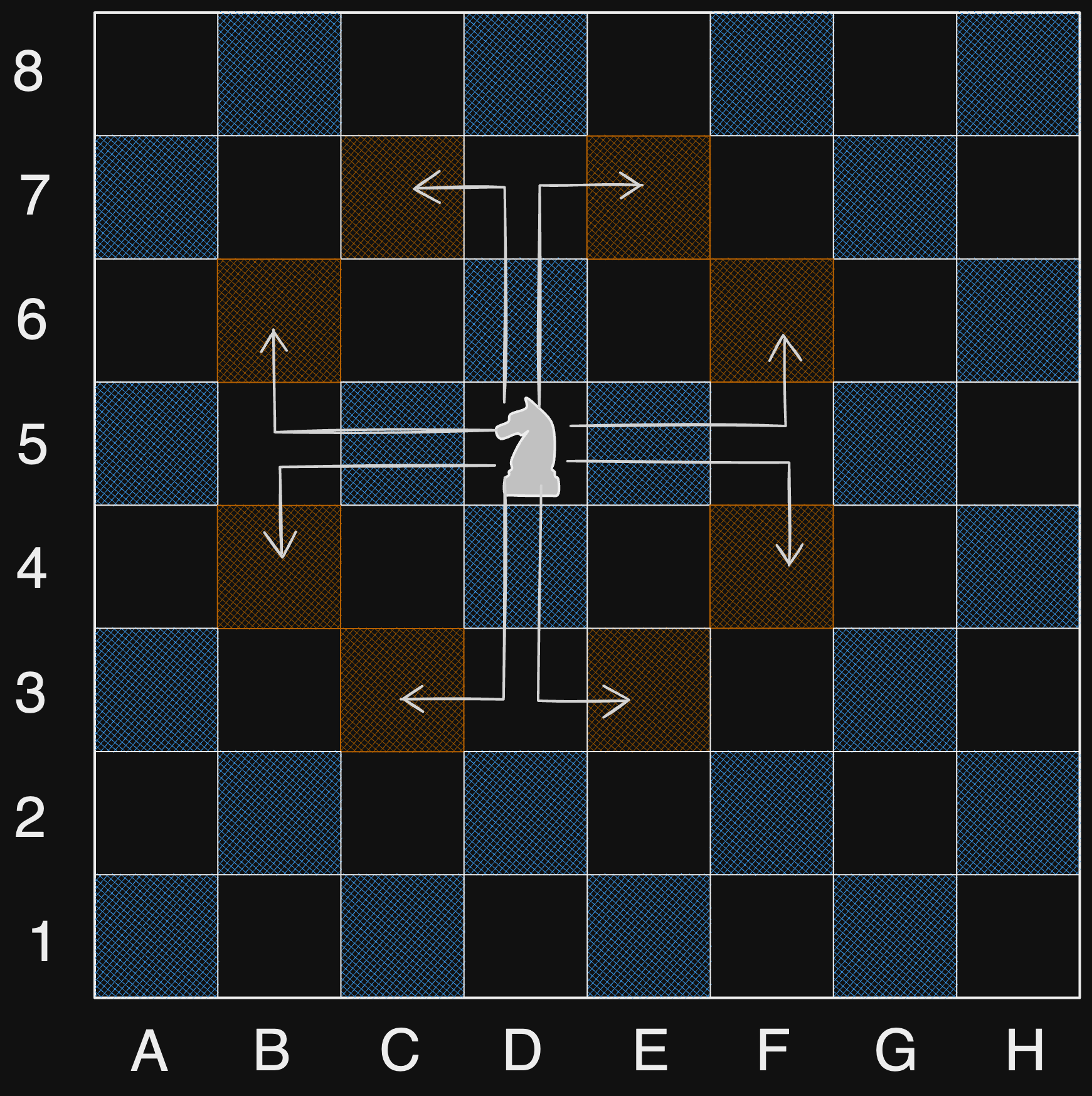
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.

The knight continues moving until it has made exactly k moves or has moved off the chessboard.

Return the probability that the knight remains on the board after it has stopped moving.

Examples

Example 1:

1
2
3
4
5
6
7

Input:
n = 3, k = 2, row = 0, column = 0
Output:
 0.06250
Explanation: There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.

Example 2:

1
2
3
4

Input:
n = 1, k = 0, row = 0, column = 0
Output:
 1.00000

Solution

Method 1 - Recursion (TLE)

We can start the DFS for k steps, and see what is the probability of landing in the board for each step.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

private static final int[][] DIRS = {
    {2, 1}, {2, -1}, {-2, 1}, {-2, -1},
    {1, 2}, {1, -2}, {-1, 2}, {-1, -2}
};

public double knightProbability(int n, int k, int row, int column) {
	return dfs(n, k, row, column);
}

public double dfs(int n, int k, int r, int c) {
	if (r < 0 || r > n - 1 || c < 0 || c > n-1) {
		return 0;
	}

	if (k == 0) {
		return 1;
	}

	double probability = 0;
	for(int[] dir: DIRS) {
		probability += 0.125 * dfs(n, k - 1, r + DIRS[0], c + DIRS[1]);
	}
	
	return probability;
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def knightProbability(n, k, row, column):
    # Possible moves of the knight
    moves = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]

    def dfs(n, k, row, column):
        # If out of bounds, return 0
        if row < 0 or row >= n or column < 0 or column >= n:
            return 0
        # If no more moves left, return 1
        if k == 0:
            return 1

        probability = 0
        for move in moves:
            next_row, next_column = row + move[0], column + move[1]
            probability += dfs(n, k - 1, next_row, next_column) / 8

        return probability

    return dfs(n, k, row, column)

Complexity

  • ⏰ Time complexity: O(8^k)
    • At each step, the function makes up to 8 recursive calls (one for each possible knight move).
    • The depth of the recursion is k (the number of moves).
  • 🧺 Space complexity: O(k) assuming recursion stack

Dry Run

Lets take first example for that, so we take n = 3, k = 2, row = 0, and column = 0.

So, initial call to dfs will be dfs(3, 2, 0, 0). Now, we can move using following directions:

1
2
3
4

private static final int[][] DIRS = {
     {2, 1}, {2, -1}, {-2, 1}, {-2, -1},
     {1, 2}, {1, -2}, {-1, 2}, {-1, -2}
};
First level of recursion k = 2

From 0, 0 we can move to:

  • Move(2, 1) ⇨ dfs(3, 1, 2, 1)
  • Move(2, -1) ⇨ dfs(3, 1, 2, -1) returns 0, as we are out of bounds
  • Move: (-2, 1) ⇨ returns 0, as we are out of bounds
  • Move: (-2, -1) ⇨ returns 0, as we are out of bounds
  • Move: (1, 2) ⇨ dfs(3, 1, 1, 2)
  • Move: (1, -2) ⇨ returns 0, as we are out of bounds
  • Move: (-1, 2) ⇨ returns 0, as we are out of bounds
  • Move: (-1, -2) ⇨ returns 0, as we are out of bounds
Second level of recursion k = 2
From (2, 1)

We consider all possible moves from (2, 1):

  • Move: (4, 2) returns 0, as we are out of bounds
  • Move: (4, 0) returns 0, as we are out of bounds
  • Move: (0, 2)
  • Move: (0, 0)
  • Move: (3, 3) returns 0, as we are out of bounds
  • Move: (3, -1) returns 0, as we are out of bounds
  • Move: (1, 3) returns 0, as we are out of bounds
  • Move: (1, -1) returns 0, as we are out of bounds

Now, as k is exhausted, and we return 1s:

1
2

dfs(3, 0, 0, 2) == 1  // Exact, moves exhausted, result 1
dfs(3, 0, 0, 0) == 1  // Exact, moves exhausted, result 1

Result from (2, 1) with k=1 is 2 / 8 = 0.25

From (1, 2)

We consider all possible moves from (1, 2):

  • Move: (3, 3) returns 0, as we are out of bounds
  • Move: (3, 1) returns 0, as we are out of bounds
  • Move: (-1, 3) returns 0, as we are out of bounds
  • Move: (-1, 1) returns 0, as we are out of bounds
  • Move: (2, 4) returns 0, as we are out of bounds
  • Move: (2, 0)
  • Move: (0, 4) returns 0, as we are out of bounds
  • Move: (0, 0)

The recursive calls:

1
2

dfs(3, 0, 2, 0) == 1  // Exact, moves exhausted, result 1
dfs(3, 0, 0, 0) == 1  // Exact, moves exhausted, result 1

Result from (1, 2) with k=1 is 2 / 8 = 0.25

First level of recursion summary

Combining the results from non-out-of-bounds moves at k=2 from (0,0):

1

 dfs(3, 2, 0, 0) = (0.25 + 0.25) / 8  * 8  = 0.50 / 8 = 0.125
Final result

We return 0.125 based on this.

Method 2 - Top Down DP

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

private static final int[][] DIRS = new int[][]{{-2,-1},{-1,-2},{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1}};

public double knightProbability(int n, int k, int row, int column) {
	return dfs(n, k, row, column, new double[n][n][k + 1]);
}

public double dfs(int n, int k, int r, int c, double[][][] dp) {
	if (r < 0 || r > n - 1 || c < 0 || c > n-1) {
		return 0;
	}

	if (k == 0) {
		return 1;
	}

	if(dp[r][c][k] != 0) {
		return dp[r][c][k];
	}

	double probability = 0;
	for(int[] dir: DIRS) {
		probability += 0.125*dfs(n, k - 1, r + dir[0], c + dir[1], dp);
	}
	dp[r][c][k] = probability;
	
	return probability;
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def knightProbability(n, k, row, column):
    # Possible moves of the knight
    moves = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]
    memo = {}

    def dfs(n, k, row, column):
        # If out of bounds, return 0
        if row < 0 or row >= n or column < 0 or column >= n:
            return 0
        # If no more moves left, return 1
        if k == 0:
            return 1
        # Check if the result is already calculated
        if (k, row, column) in memo:
            return memo[(k, row, column)]

        probability = 0
        for move in moves:
            next_row, next_column = row + move[0], column + move[1]
            probability += dfs(n, k - 1, next_row, next_column) / 8

        memo[(k, row, column)] = probability
        return probability

    return dfs(n, k, row, column)

Complexity

  • Time: O(n^2*k)
    • The number of unique states is determined by the combination of k, row, and column.
    • The number of possible values for row and column is n, and the number of possible values for k is k + 1.
    • So the total number of unique states is ( n \times n \times (k + 1) ).
    • For each state, we explore up to 8 possible moves, making up to 8 recursive calls. However, due to memoization, each state is only computed once.
  • Space: O(n^2*k) for using memoization table (and also O(k) assuming recursion stack)

Method 3 - Bottom up DP

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

private static final int[][] DIRS = new int[][]{{-2,-1},{-1,-2},{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1}};

	public double knightProbability(int n, int k, int row, int column) {
		double[][][] dp = new double[k + 1][n][n];
		dp[0][row][column] = 1;

		for (int step = 1; step <= k; step++) {
			for (int r = 0; r < n; r++) {
				for (int c = 0; c < n; c++) {
					if (dp[step - 1][r][c] > 0) {
						for (int[] direction: directions) {
							int nextRow = r + direction[0];
							int nextColumn = c + direction[1];

							if (nextRow >= 0 && nextRow < n && nextColumn >= 0 && nextColumn  <  n) {
								dp[step][nextRow][nextColumn] += dp[step - 1][r][c] / 8.0;
							}
						}
					}
				}
			}
		}

		double finalProbability = 0;

		for (int r = 0; r < n; r++) {
			for (int c = 0; c < n; c++) {
				finalProbability += dp[k][r][c];
			}
		}

		return finalProbability;
	}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def knightProbability(n, k, row, column):
    # Possible moves of the knight
    moves = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]

    # dp array to store the probabilities
    dp = [[[0] * n for _ in range(n)] for _ in range(k + 1)]
    dp[0][row][column] = 1  # Initial position, 0 moves left

    for step in range(1, k + 1):
        for r in range(n):
            for c in range(n):
                for move in moves:
                    prev_row, prev_column = r + move[0], c + move[1]
                    if 0 <= prev_row < n and 0 <= prev_column < n:
                        dp[step][r][c] += dp[step - 1][prev_row][prev_column] / 8

    # Calculate the final probability
    final_probability = 0
    for r in range(n):
        for c in range(n):
            final_probability += dp[k][r][c]

    return final_probability

Complexity

  • Time: O(n^2*k)
  • Space: O(n^2*k)