problemhardalgorithmsleetcode-1483leetcode 1483leetcode1483

Kth Ancestor of a Tree Node

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of ith node. The root of the tree is node 0. Find the kth ancestor of a given node.

The kth ancestor of a tree node is the kth node in the path from that node to the root node.

Implement the TreeAncestor class:

  • TreeAncestor(int n, int[] parent) Initializes the object with the number of nodes in the tree and the parent array.
  • int getKthAncestor(int node, int k) return the kth ancestor of the given node node. If there is no such ancestor, return -1.

Examples

Example 1

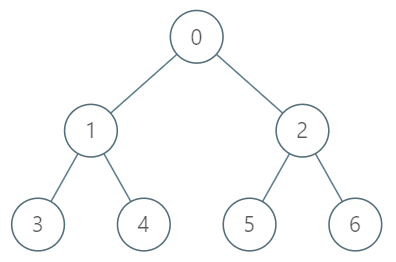
Input
["TreeAncestor", "getKthAncestor", "getKthAncestor", "getKthAncestor"]
[[7, [-1, 0, 0, 1, 1, 2, 2]], [3, 1], [5, 2], [6, 3]]
Output
[null, 1, 0, -1]

Explanation
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor

Constraints

  • 1 <= k <= n <= 5 * 104
  • parent.length == n
  • parent[0] == -1
  • 0 <= parent[i] < n for all 0 < i < n
  • 0 <= node < n
  • There will be at most 5 * 104 queries.

Solution

Method 1 – Binary Lifting (Dynamic Programming)

Intuition

Precompute ancestors for each node at powers of two distances, so we can jump up the tree in logarithmic steps. This allows efficient queries for the kth ancestor.

Approach

  1. Build a table up[node][j] where up[node][j] is the 2^j-th ancestor of node.
  2. For each query, repeatedly jump up by the largest possible power of two less than or equal to k.
  3. If at any point the ancestor is -1, return -1.

Code

C++
class TreeAncestor {
    vector<vector<int>> up;
    int LOG;
public:
    TreeAncestor(int n, vector<int>& parent) {
        LOG = 0;
        int tmp = n;
        while (tmp) { LOG++; tmp >>= 1; }
        up.assign(n, vector<int>(LOG, -1));
        for (int i = 0; i < n; ++i) up[i][0] = parent[i];
        for (int j = 1; j < LOG; ++j)
            for (int i = 0; i < n; ++i)
                up[i][j] = up[i][j-1] == -1 ? -1 : up[up[i][j-1]][j-1];
    }
    int getKthAncestor(int node, int k) {
        for (int j = 0; j < LOG && node != -1; ++j)
            if (k & (1 << j)) node = up[node][j];
        return node;
    }
};
Go
type TreeAncestor struct {
    up [][]int
    log int
}

func Constructor(n int, parent []int) TreeAncestor {
    log := 0
    for tmp := n; tmp > 0; tmp >>= 1 { log++ }
    up := make([][]int, n)
    for i := range up {
        up[i] = make([]int, log)
        up[i][0] = parent[i]
    }
    for j := 1; j < log; j++ {
        for i := 0; i < n; i++ {
            if up[i][j-1] == -1 {
                up[i][j] = -1
            } else {
                up[i][j] = up[up[i][j-1]][j-1]
            }
        }
    }
    return TreeAncestor{up, log}
}

func (t *TreeAncestor) GetKthAncestor(node int, k int) int {
    for j := 0; j < t.log && node != -1; j++ {
        if k&(1<<j) > 0 {
            node = t.up[node][j]
        }
    }
    return node
}
Java
class TreeAncestor {
    int[][] up;
    int LOG;
    public TreeAncestor(int n, int[] parent) {
        LOG = 0;
        int tmp = n;
        while (tmp > 0) { LOG++; tmp >>= 1; }
        up = new int[n][LOG];
        for (int i = 0; i < n; ++i) up[i][0] = parent[i];
        for (int j = 1; j < LOG; ++j)
            for (int i = 0; i < n; ++i)
                up[i][j] = up[i][j-1] == -1 ? -1 : up[up[i][j-1]][j-1];
    }
    public int getKthAncestor(int node, int k) {
        for (int j = 0; j < LOG && node != -1; ++j)
            if ((k & (1 << j)) != 0) node = up[node][j];
        return node;
    }
}
Kotlin
class TreeAncestor(n: Int, parent: IntArray) {
    private val LOG = Integer.SIZE - Integer.numberOfLeadingZeros(n)
    private val up = Array(n) { IntArray(LOG) }
    init {
        for (i in 0 until n) up[i][0] = parent[i]
        for (j in 1 until LOG)
            for (i in 0 until n)
                up[i][j] = if (up[i][j-1] == -1) -1 else up[up[i][j-1]][j-1]
    }
    fun getKthAncestor(node: Int, k: Int): Int {
        var v = node
        for (j in 0 until LOG) {
            if ((k shr j) and 1 == 1) v = if (v == -1) -1 else up[v][j]
        }
        return v
    }
}
Python
class TreeAncestor:
    def __init__(self, n: int, parent: list[int]):
        self.LOG = n.bit_length()
        self.up = [[-1]*self.LOG for _ in range(n)]
        for i in range(n):
            self.up[i][0] = parent[i]
        for j in range(1, self.LOG):
            for i in range(n):
                prev = self.up[i][j-1]
                self.up[i][j] = -1 if prev == -1 else self.up[prev][j-1]
    def getKthAncestor(self, node: int, k: int) -> int:
        for j in range(self.LOG):
            if k & (1 << j):
                node = self.up[node][j]
                if node == -1:
                    break
        return node
Rust
struct TreeAncestor {
    up: Vec<Vec<i32>>,
    log: usize,
}
impl TreeAncestor {
    fn new(n: i32, parent: Vec<i32>) -> Self {
        let log = 32 - n.leading_zeros() as usize;
        let mut up = vec![vec![-1; log]; n as usize];
        for i in 0..n as usize { up[i][0] = parent[i]; }
        for j in 1..log {
            for i in 0..n as usize {
                let prev = up[i][j-1];
                up[i][j] = if prev == -1 { -1 } else { up[prev as usize][j-1] };
            }
        }
        TreeAncestor { up, log }
    }
    fn get_kth_ancestor(&self, mut node: i32, k: i32) -> i32 {
        for j in 0..self.log {
            if (k & (1 << j)) != 0 {
                node = if node == -1 { -1 } else { self.up[node as usize][j] };
            }
        }
        node
    }
}
TypeScript
class TreeAncestor {
    private up: number[][];
    private LOG: number;
    constructor(n: number, parent: number[]) {
        this.LOG = Math.ceil(Math.log2(n + 1));
        this.up = Array.from({length: n}, () => Array(this.LOG).fill(-1));
        for (let i = 0; i < n; ++i) this.up[i][0] = parent[i];
        for (let j = 1; j < this.LOG; ++j)
            for (let i = 0; i < n; ++i)
                this.up[i][j] = this.up[i][j-1] === -1 ? -1 : this.up[this.up[i][j-1]][j-1];
    }
    getKthAncestor(node: number, k: number): number {
        for (let j = 0; j < this.LOG && node !== -1; ++j)
            if (k & (1 << j)) node = this.up[node][j];
        return node;
    }
}

Complexity

  • ⏰ Time complexity: O(log n) per query, O(n log n) preprocessing. Each query jumps up the tree in logarithmic steps.
  • 🧺 Space complexity: O(n log n) for ancestor table.

Comments