Kth Smallest Number in Multiplication Table

Problem

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return thekth smallest element in them x n multiplication table.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2021/05/02/multtable1-grid.jpg)

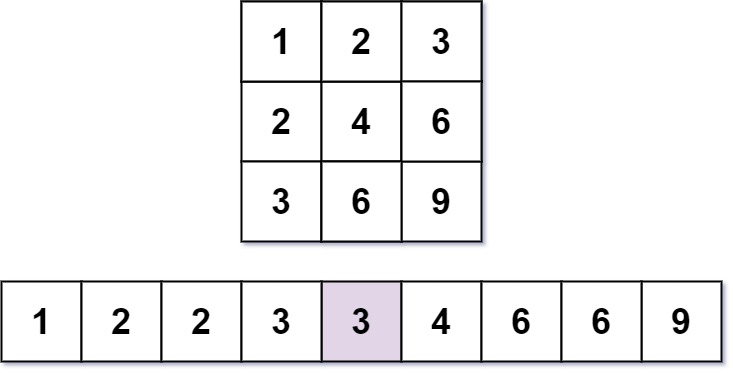
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.

Example 2

![](https://assets.leetcode.com/uploads/2021/05/02/multtable2-grid.jpg)

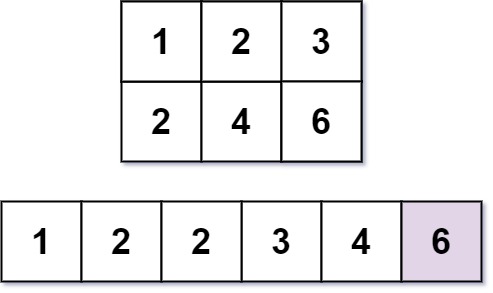
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.

Constraints

• 1 <= m, n <= 3 * 10^4
• 1 <= k <= m * n

Solution

Method 1 – Binary Search on Value

Intuition

The multiplication table is sorted in each row and column. To find the k-th smallest number, we can use binary search on the value range. For a candidate value x, count how many numbers in the table are ≤ x. If the count is at least k, x could be the answer.

Approach

1. Set left = 1, right = m * n (the largest value in the table).
2. While left < right:
   • Compute mid = (left + right) // 2.
   • For each row i, count how many numbers ≤ mid (which is min(mid // i, n)).
   • Sum the counts for all rows.
   • If the count ≥ k, set right = mid; else, set left = mid + 1.
3. Return left as the answer.

Code

C++

class Solution {
public:
    int findKthNumber(int m, int n, int k) {
        int l = 1, r = m * n;
        while (l < r) {
            int mid = (l + r) / 2, cnt = 0;
            for (int i = 1; i <= m; ++i) cnt += min(mid / i, n);
            if (cnt >= k) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};

Go

func findKthNumber(m int, n int, k int) int {
    l, r := 1, m*n
    for l < r {
        mid := (l + r) / 2
        cnt := 0
        for i := 1; i <= m; i++ {
            cnt += min(mid/i, n)
        }
        if cnt >= k {
            r = mid
        } else {
            l = mid + 1
        }
    }
    return l
}
func min(a, b int) int { if a < b { return a }; return b }

Java

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int l = 1, r = m * n;
        while (l < r) {
            int mid = (l + r) / 2, cnt = 0;
            for (int i = 1; i <= m; ++i) cnt += Math.min(mid / i, n);
            if (cnt >= k) r = mid;
            else l = mid + 1;
        }
        return l;
    }
}

Kotlin

class Solution {
    fun findKthNumber(m: Int, n: Int, k: Int): Int {
        var l = 1
        var r = m * n
        while (l < r) {
            val mid = (l + r) / 2
            var cnt = 0
            for (i in 1..m) cnt += minOf(mid / i, n)
            if (cnt >= k) r = mid else l = mid + 1
        }
        return l
    }
}

Python

class Solution:
    def findKthNumber(self, m: int, n: int, k: int) -> int:
        l, r = 1, m * n
        while l < r:
            mid = (l + r) // 2
            cnt = sum(min(mid // i, n) for i in range(1, m+1))
            if cnt >= k:
                r = mid
            else:
                l = mid + 1
        return l

Rust

impl Solution {
    pub fn find_kth_number(m: i32, n: i32, k: i32) -> i32 {
        let (mut l, mut r) = (1, m * n);
        while l < r {
            let mid = (l + r) / 2;
            let mut cnt = 0;
            for i in 1..=m {
                cnt += (mid / i).min(n);
            }
            if cnt >= k { r = mid; } else { l = mid + 1; }
        }
        l
    }
}

TypeScript

class Solution {
    findKthNumber(m: number, n: number, k: number): number {
        let l = 1, r = m * n;
        while (l < r) {
            const mid = Math.floor((l + r) / 2);
            let cnt = 0;
            for (let i = 1; i <= m; ++i) cnt += Math.min(Math.floor(mid / i), n);
            if (cnt >= k) r = mid;
            else l = mid + 1;
        }
        return l;
    }
}

Complexity

• ⏰ Time complexity: O(m log(mn)), where m is the number of rows. Each binary search step checks all rows.
• 🧺 Space complexity: O(1), only a few variables are used.