Problem

A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.

Given an m x n integer grid, return _thesize (i.e., the side length _k ) of thelargest magic square that can be found within this grid.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


![](https://assets.leetcode.com/uploads/2021/05/29/magicsquare-grid.jpg)

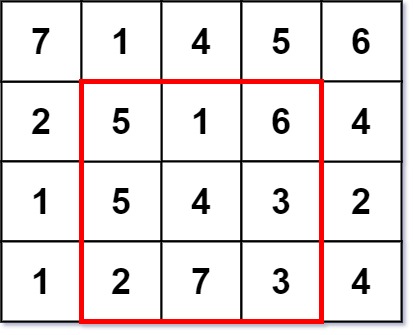
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12

Example 2

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2021/05/29/magicsquare2-grid.jpg)

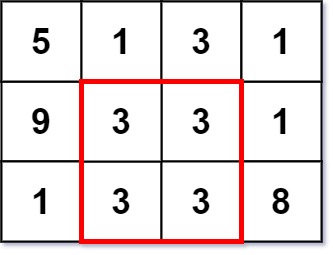
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • 1 <= grid[i][j] <= 10^6

Solution

Method 1 – Prefix Sums and Brute Force

Intuition

A magic square requires all rows, columns, and both diagonals to have the same sum. We can use prefix sums to quickly compute row and column sums for any sub-square, and then check all possible k x k squares from largest to smallest.

Approach

  1. Precompute prefix sums for rows and columns.
  2. For k from min(m, n) down to 1:
    • For each possible top-left corner (i, j), check the k x k square:
      • Compute the target sum as the sum of the first row.
      • Check all rows, columns, and both diagonals for equality to the target sum using prefix sums.
      • If valid, return k.
  3. If no larger square is found, return 1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    int largestMagicSquare(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> row(m, vector<int>(n+1)), col(m+1, vector<int>(n));
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j) {
                row[i][j+1] = row[i][j] + grid[i][j];
                col[i+1][j] = col[i][j] + grid[i][j];
            }
        for (int k = min(m, n); k >= 1; --k) {
            for (int i = 0; i <= m-k; ++i) {
                for (int j = 0; j <= n-k; ++j) {
                    int sum = row[i][j+k] - row[i][j];
                    bool ok = true;
                    for (int x = 0; x < k; ++x) {
                        if (row[i+x][j+k] - row[i+x][j] != sum) ok = false;
                        if (col[i+k][j+x] - col[i][j+x] != sum) ok = false;
                    }
                    int d1 = 0, d2 = 0;
                    for (int x = 0; x < k; ++x) {
                        d1 += grid[i+x][j+x];
                        d2 += grid[i+x][j+k-1-x];
                    }
                    if (d1 != sum || d2 != sum) ok = false;
                    if (ok) return k;
                }
            }
        }
        return 1;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

func largestMagicSquare(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    row := make([][]int, m)
    col := make([][]int, m+1)
    for i := range row { row[i] = make([]int, n+1) }
    for i := range col { col[i] = make([]int, n) }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            row[i][j+1] = row[i][j] + grid[i][j]
            col[i+1][j] = col[i][j] + grid[i][j]
        }
    }
    for k := min(m, n); k >= 1; k-- {
        for i := 0; i <= m-k; i++ {
            for j := 0; j <= n-k; j++ {
                sum := row[i][j+k] - row[i][j]
                ok := true
                for x := 0; x < k; x++ {
                    if row[i+x][j+k]-row[i+x][j] != sum { ok = false }
                    if col[i+k][j+x]-col[i][j+x] != sum { ok = false }
                }
                d1, d2 := 0, 0
                for x := 0; x < k; x++ {
                    d1 += grid[i+x][j+x]
                    d2 += grid[i+x][j+k-1-x]
                }
                if d1 != sum || d2 != sum { ok = false }
                if ok { return k }
            }
        }
    }
    return 1
}
func min(a, b int) int { if a < b { return a }; return b }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    public int largestMagicSquare(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] row = new int[m][n+1], col = new int[m+1][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j) {
                row[i][j+1] = row[i][j] + grid[i][j];
                col[i+1][j] = col[i][j] + grid[i][j];
            }
        for (int k = Math.min(m, n); k >= 1; --k) {
            for (int i = 0; i <= m-k; ++i) {
                for (int j = 0; j <= n-k; ++j) {
                    int sum = row[i][j+k] - row[i][j];
                    boolean ok = true;
                    for (int x = 0; x < k; ++x) {
                        if (row[i+x][j+k] - row[i+x][j] != sum) ok = false;
                        if (col[i+k][j+x] - col[i][j+x] != sum) ok = false;
                    }
                    int d1 = 0, d2 = 0;
                    for (int x = 0; x < k; ++x) {
                        d1 += grid[i+x][j+x];
                        d2 += grid[i+x][j+k-1-x];
                    }
                    if (d1 != sum || d2 != sum) ok = false;
                    if (ok) return k;
                }
            }
        }
        return 1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    fun largestMagicSquare(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        val row = Array(m) { IntArray(n+1) }
        val col = Array(m+1) { IntArray(n) }
        for (i in 0 until m)
            for (j in 0 until n) {
                row[i][j+1] = row[i][j] + grid[i][j]
                col[i+1][j] = col[i][j] + grid[i][j]
            }
        for (k in minOf(m, n) downTo 1) {
            for (i in 0..m-k) {
                for (j in 0..n-k) {
                    val sum = row[i][j+k] - row[i][j]
                    var ok = true
                    for (x in 0 until k) {
                        if (row[i+x][j+k] - row[i+x][j] != sum) ok = false
                        if (col[i+k][j+x] - col[i][j+x] != sum) ok = false
                    }
                    var d1 = 0; var d2 = 0
                    for (x in 0 until k) {
                        d1 += grid[i+x][j+x]
                        d2 += grid[i+x][j+k-1-x]
                    }
                    if (d1 != sum || d2 != sum) ok = false
                    if (ok) return k
                }
            }
        }
        return 1
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def largestMagicSquare(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        row = [[0]*(n+1) for _ in range(m)]
        col = [[0]*n for _ in range(m+1)]
        for i in range(m):
            for j in range(n):
                row[i][j+1] = row[i][j] + grid[i][j]
                col[i+1][j] = col[i][j] + grid[i][j]
        for k in range(min(m, n), 0, -1):
            for i in range(m-k+1):
                for j in range(n-k+1):
                    s = row[i][j+k] - row[i][j]
                    ok = True
                    for x in range(k):
                        if row[i+x][j+k] - row[i+x][j] != s: ok = False
                        if col[i+k][j+x] - col[i][j+x] != s: ok = False
                    d1 = d2 = 0
                    for x in range(k):
                        d1 += grid[i+x][j+x]
                        d2 += grid[i+x][j+k-1-x]
                    if d1 != s or d2 != s: ok = False
                    if ok: return k
        return 1
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

impl Solution {
    pub fn largest_magic_square(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut row = vec![vec![0; n+1]; m];
        let mut col = vec![vec![0; n]; m+1];
        for i in 0..m {
            for j in 0..n {
                row[i][j+1] = row[i][j] + grid[i][j];
                col[i+1][j] = col[i][j] + grid[i][j];
            }
        }
        for k in (1..=m.min(n)).rev() {
            for i in 0..=m-k {
                for j in 0..=n-k {
                    let sum = row[i][j+k] - row[i][j];
                    let mut ok = true;
                    for x in 0..k {
                        if row[i+x][j+k] - row[i+x][j] != sum { ok = false; }
                        if col[i+k][j+x] - col[i][j+x] != sum { ok = false; }
                    }
                    let (mut d1, mut d2) = (0, 0);
                    for x in 0..k {
                        d1 += grid[i+x][j+x];
                        d2 += grid[i+x][j+k-1-x];
                    }
                    if d1 != sum || d2 != sum { ok = false; }
                    if ok { return k as i32; }
                }
            }
        }
        1
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    largestMagicSquare(grid: number[][]): number {
        const m = grid.length, n = grid[0].length;
        const row = Array.from({length: m}, () => Array(n+1).fill(0));
        const col = Array.from({length: m+1}, () => Array(n).fill(0));
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j) {
                row[i][j+1] = row[i][j] + grid[i][j];
                col[i+1][j] = col[i][j] + grid[i][j];
            }
        for (let k = Math.min(m, n); k >= 1; --k) {
            for (let i = 0; i <= m-k; ++i) {
                for (let j = 0; j <= n-k; ++j) {
                    const sum = row[i][j+k] - row[i][j];
                    let ok = true;
                    for (let x = 0; x < k; ++x) {
                        if (row[i+x][j+k] - row[i+x][j] !== sum) ok = false;
                        if (col[i+k][j+x] - col[i][j+x] !== sum) ok = false;
                    }
                    let d1 = 0, d2 = 0;
                    for (let x = 0; x < k; ++x) {
                        d1 += grid[i+x][j+x];
                        d2 += grid[i+x][j+k-1-x];
                    }
                    if (d1 !== sum || d2 !== sum) ok = false;
                    if (ok) return k;
                }
            }
        }
        return 1;
    }
}

Complexity

  • ⏰ Time complexity: O(m * n * min(m, n)^2), where m and n are grid dimensions. For each k, we check all possible k x k squares.
  • 🧺 Space complexity: O(m * n), for prefix sums.