problemmediumalgorithmsleetcode-1727leetcode 1727leetcode1727

Largest Submatrix With Rearrangements

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix withinmatrix _whereevery element of the submatrix is _1 after reordering the columns optimally.

Examples

Example 1


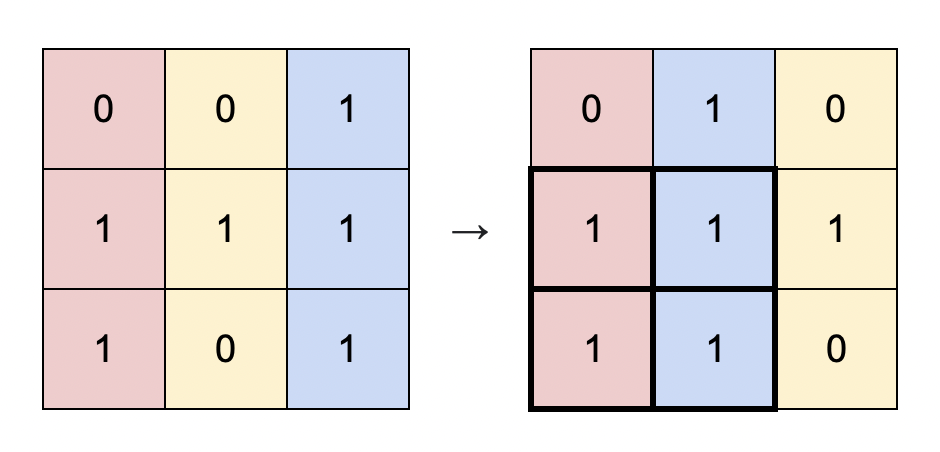
![](https://assets.leetcode.com/uploads/2020/12/29/screenshot-2020-12-30-at-40536-pm.png)

Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2


![](https://assets.leetcode.com/uploads/2020/12/29/screenshot-2020-12-30-at-40852-pm.png)

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

Constraints

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m * n <= 10^5
  • matrix[i][j] is either 0 or 1.

Solution

Method 1 – Histogram and Greedy Sorting

Intuition

For each row, treat the number of consecutive 1's above (including itself) as a histogram. By sorting each row's histogram in descending order, we can greedily maximize the area of a submatrix of 1's after rearranging columns.

Approach

  1. For each cell, compute the height of consecutive 1's above (including itself).
  2. For each row, sort the histogram heights in descending order.
  3. For each position in the sorted row, calculate the area as height * (index+1).
  4. Track and return the maximum area found.

Code

C++
class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size(), ans = 0;
        for (int i = 1; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (matrix[i][j]) matrix[i][j] += matrix[i-1][j];
        for (auto& row : matrix) {
            vector<int> h = row;
            sort(h.rbegin(), h.rend());
            for (int j = 0; j < n; ++j)
                ans = max(ans, h[j] * (j+1));
        }
        return ans;
    }
};
Go
func largestSubmatrix(matrix [][]int) int {
    m, n := len(matrix), len(matrix[0])
    ans := 0
    for i := 1; i < m; i++ {
        for j := 0; j < n; j++ {
            if matrix[i][j] == 1 {
                matrix[i][j] += matrix[i-1][j]
            }
        }
    }
    for _, row := range matrix {
        h := append([]int(nil), row...)
        sort.Sort(sort.Reverse(sort.IntSlice(h)))
        for j := 0; j < n; j++ {
            if h[j]*(j+1) > ans { ans = h[j]*(j+1) }
        }
    }
    return ans
}
Java
class Solution {
    public int largestSubmatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length, ans = 0;
        for (int i = 1; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (matrix[i][j] == 1) matrix[i][j] += matrix[i-1][j];
        for (int[] row : matrix) {
            int[] h = row.clone();
            Arrays.sort(h);
            for (int j = 0; j < n; ++j)
                ans = Math.max(ans, h[n-1-j] * (j+1));
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun largestSubmatrix(matrix: Array<IntArray>): Int {
        val m = matrix.size
        val n = matrix[0].size
        var ans = 0
        for (i in 1 until m)
            for (j in 0 until n)
                if (matrix[i][j] == 1) matrix[i][j] += matrix[i-1][j]
        for (row in matrix) {
            val h = row.copyOf()
            h.sortDescending()
            for (j in 0 until n)
                ans = maxOf(ans, h[j] * (j+1))
        }
        return ans
    }
}
Python
class Solution:
    def largestSubmatrix(self, matrix: list[list[int]]) -> int:
        m, n = len(matrix), len(matrix[0])
        for i in range(1, m):
            for j in range(n):
                if matrix[i][j]:
                    matrix[i][j] += matrix[i-1][j]
        ans = 0
        for row in matrix:
            h = sorted(row, reverse=True)
            for j, v in enumerate(h):
                ans = max(ans, v * (j+1))
        return ans
Rust
impl Solution {
    pub fn largest_submatrix(matrix: Vec<Vec<i32>>) -> i32 {
        let m = matrix.len();
        let n = matrix[0].len();
        let mut mat = matrix.clone();
        for i in 1..m {
            for j in 0..n {
                if mat[i][j] != 0 {
                    mat[i][j] += mat[i-1][j];
                }
            }
        }
        let mut ans = 0;
        for row in mat.iter_mut() {
            row.sort_by(|a, b| b.cmp(a));
            for (j, &v) in row.iter().enumerate() {
                ans = ans.max(v * (j as i32 + 1));
            }
        }
        ans
    }
}
TypeScript
class Solution {
    largestSubmatrix(matrix: number[][]): number {
        const m = matrix.length, n = matrix[0].length
        for (let i = 1; i < m; ++i)
            for (let j = 0; j < n; ++j)
                if (matrix[i][j]) matrix[i][j] += matrix[i-1][j]
        let ans = 0
        for (const row of matrix) {
            const h = [...row].sort((a, b) => b - a)
            for (let j = 0; j < n; ++j)
                ans = Math.max(ans, h[j] * (j+1))
        }
        return ans
    }
}

Complexity

  • ⏰ Time complexity: O(m*n*log n), where m and n are matrix dimensions. Each row is sorted.
  • 🧺 Space complexity: O(n), for sorting each row.

Comments