problemeasyalgorithmsleetcode-812leetcode 812leetcode812

Largest Triangle Area

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10-5 of the actual answer will be accepted.

Examples

Example 1


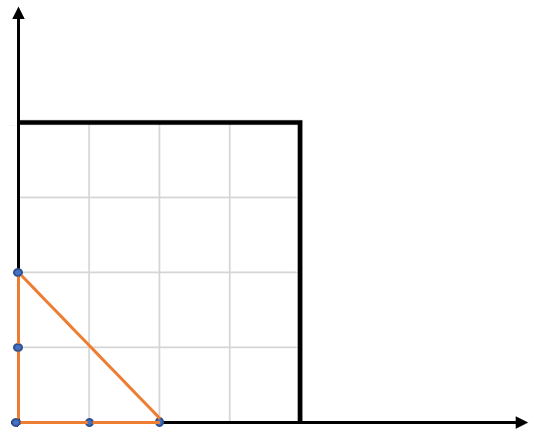
![](https://s3-lc-upload.s3.amazonaws.com/uploads/2018/04/04/1027.png)

Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2.00000
Explanation: The five points are shown in the above figure. The red triangle is the largest.

Example 2

Input: points = [[1,0],[0,0],[0,1]]
Output: 0.50000

Constraints

  • 3 <= points.length <= 50
  • -50 <= xi, yi <= 50
  • All the given points are unique.

Solution

Method 1 – Brute Force with Shoelace Formula

Intuition

The area of a triangle given three points can be computed using the shoelace formula. Try all possible triplets and keep the maximum area found.

Approach

  1. For every combination of three different points, calculate the area using the formula:
    • Area = 0.5 * |x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|
  2. Track the maximum area found.
  3. Return the maximum area (as a float/double).

Code

C++
class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        double ans = 0;
        int n = points.size();
        for (int i = 0; i < n; ++i)
            for (int j = i+1; j < n; ++j)
                for (int k = j+1; k < n; ++k) {
                    double area = abs(points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])) / 2.0;
                    ans = max(ans, area);
                }
        return ans;
    }
};
Go
func largestTriangleArea(points [][]int) float64 {
    ans := 0.0
    n := len(points)
    for i := 0; i < n; i++ {
        for j := i+1; j < n; j++ {
            for k := j+1; k < n; k++ {
                area := 0.5 * math.Abs(float64(points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])))
                if area > ans { ans = area }
            }
        }
    }
    return ans
}
Java
class Solution {
    public double largestTriangleArea(int[][] points) {
        double ans = 0;
        int n = points.length;
        for (int i = 0; i < n; ++i)
            for (int j = i+1; j < n; ++j)
                for (int k = j+1; k < n; ++k) {
                    double area = Math.abs(points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])) / 2.0;
                    ans = Math.max(ans, area);
                }
        return ans;
    }
}
Kotlin
class Solution {
    fun largestTriangleArea(points: Array<IntArray>): Double {
        var ans = 0.0
        val n = points.size
        for (i in 0 until n)
            for (j in i+1 until n)
                for (k in j+1 until n) {
                    val area = Math.abs(points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])) / 2.0
                    ans = maxOf(ans, area)
                }
        return ans
    }
}
Python
class Solution:
    def largestTriangleArea(self, points: list[list[int]]) -> float:
        from itertools import combinations
        ans = 0.0
        for a, b, c in combinations(points, 3):
            area = abs(a[0]*(b[1]-c[1]) + b[0]*(c[1]-a[1]) + c[0]*(a[1]-b[1])) / 2
            ans = max(ans, area)
        return ans
Rust
impl Solution {
    pub fn largest_triangle_area(points: Vec<Vec<i32>>) -> f64 {
        let mut ans = 0.0;
        let n = points.len();
        for i in 0..n {
            for j in i+1..n {
                for k in j+1..n {
                    let area = ((points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])) as f64).abs() / 2.0;
                    if area > ans { ans = area; }
                }
            }
        }
        ans
    }
}
TypeScript
class Solution {
    largestTriangleArea(points: number[][]): number {
        let ans = 0
        const n = points.length
        for (let i = 0; i < n; ++i)
            for (let j = i+1; j < n; ++j)
                for (let k = j+1; k < n; ++k) {
                    const area = Math.abs(points[i][0]*(points[j][1]-points[k][1]) + points[j][0]*(points[k][1]-points[i][1]) + points[k][0]*(points[i][1]-points[j][1])) / 2
                    ans = Math.max(ans, area)
                }
        return ans
    }
}

Complexity

  • ⏰ Time complexity: O(n^3), where n is the number of points. All triplets are checked.
  • 🧺 Space complexity: O(1), only a few variables are used.

Comments