Problem

There is a 1-based binary matrix where 0 represents land and 1 represents water. You are given integers row and col representing the number of rows and columns in the matrix, respectively.

Initially on day 0, the entire matrix is land. However, each day a new cell becomes flooded with water. You are given a 1-based 2D array cells, where cells[i] = [ri, ci] represents that on the ith day, the cell on the rith row and cith column (1-based coordinates) will be covered with water (i.e., changed to 1).

You want to find the last day that it is possible to walk from the top to the bottom by only walking on land cells. You can start from any cell in the top row and end at any cell in the bottom row. You can only travel in thefour cardinal directions (left, right, up, and down).

Return thelast day where it is possible to walk from the top to the bottom by only walking on land cells.

Examples

Example 1

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2021/07/27/1.png)

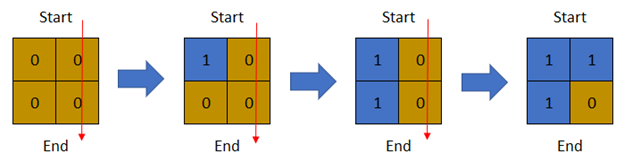
Input: row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
Output: 2
Explanation: The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 2.

Example 2

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2021/07/27/2.png)

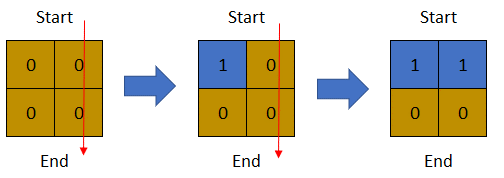
Input: row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
Output: 1
Explanation: The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 1.

Example 3

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2021/07/27/3.png)

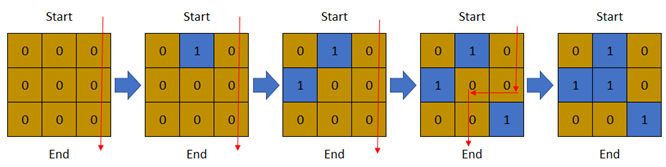
Input: row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
Output: 3
Explanation: The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 3.

Constraints

  • 2 <= row, col <= 2 * 10^4
  • 4 <= row * col <= 2 * 10^4
  • cells.length == row * col
  • 1 <= ri <= row
  • 1 <= ci <= col
  • All the values of cells are unique.

Solution

Method 1 – Binary Search + BFS

Intuition

We want to find the last day we can cross from the top to the bottom row before water blocks all possible paths. Since the process is monotonic (once a cell is flooded, it stays flooded), we can use binary search to efficiently find the answer. For each day, we check if a path exists using BFS.

Approach

  1. Use binary search on the number of days (from 0 to len(cells)-1).
  2. For each mid day, flood the first mid cells and check if a path exists from the top to the bottom row using BFS.
  3. If a path exists, try a later day; otherwise, try an earlier day.
  4. Return the last day where crossing is possible.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    int latestDayToCross(int row, int col, vector<vector<int>>& cells) {
        int l = 0, r = cells.size() - 1, ans = 0;
        vector<vector<int>> dirs = {{0,1},{1,0},{0,-1},{-1,0}};
        auto canCross = [&](int day) {
            vector<vector<int>> grid(row, vector<int>(col, 0));
            for (int i = 0; i <= day; ++i) grid[cells[i][0]-1][cells[i][1]-1] = 1;
            queue<pair<int,int>> q;
            vector<vector<bool>> vis(row, vector<bool>(col, false));
            for (int j = 0; j < col; ++j) if (!grid[0][j]) { q.push({0,j}); vis[0][j] = true; }
            while (!q.empty()) {
                auto [x, y] = q.front(); q.pop();
                if (x == row-1) return true;
                for (auto& d : dirs) {
                    int nx = x + d[0], ny = y + d[1];
                    if (nx >= 0 && nx < row && ny >= 0 && ny < col && !grid[nx][ny] && !vis[nx][ny]) {
                        vis[nx][ny] = true;
                        q.push({nx, ny});
                    }
                }
            }
            return false;
        };
        while (l <= r) {
            int m = l + (r-l)/2;
            if (canCross(m)) { ans = m; l = m+1; }
            else r = m-1;
        }
        return ans+1;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

func latestDayToCross(row int, col int, cells [][]int) int {
    dirs := [][]int{{0,1},{1,0},{0,-1},{-1,0}}
    canCross := func(day int) bool {
        grid := make([][]int, row)
        for i := range grid { grid[i] = make([]int, col) }
        for i := 0; i <= day; i++ { grid[cells[i][0]-1][cells[i][1]-1] = 1 }
        vis := make([][]bool, row)
        for i := range vis { vis[i] = make([]bool, col) }
        q := [][2]int{}
        for j := 0; j < col; j++ {
            if grid[0][j] == 0 {
                q = append(q, [2]int{0, j})
                vis[0][j] = true
            }
        }
        for len(q) > 0 {
            x, y := q[0][0], q[0][1]
            q = q[1:]
            if x == row-1 { return true }
            for _, d := range dirs {
                nx, ny := x+d[0], y+d[1]
                if nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == 0 && !vis[nx][ny] {
                    vis[nx][ny] = true
                    q = append(q, [2]int{nx, ny})
                }
            }
        }
        return false
    }
    l, r, ans := 0, len(cells)-1, 0
    for l <= r {
        m := l + (r-l)/2
        if canCross(m) { ans = m; l = m+1 } else { r = m-1 }
    }
    return ans+1
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    public int latestDayToCross(int row, int col, int[][] cells) {
        int l = 0, r = cells.length-1, ans = 0;
        int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
        java.util.function.IntPredicate canCross = day -> {
            int[][] grid = new int[row][col];
            for (int i = 0; i <= day; i++) grid[cells[i][0]-1][cells[i][1]-1] = 1;
            boolean[][] vis = new boolean[row][col];
            java.util.Queue<int[]> q = new java.util.LinkedList<>();
            for (int j = 0; j < col; j++) if (grid[0][j] == 0) { q.add(new int[]{0,j}); vis[0][j] = true; }
            while (!q.isEmpty()) {
                int[] cur = q.poll();
                if (cur[0] == row-1) return true;
                for (int[] d : dirs) {
                    int nx = cur[0]+d[0], ny = cur[1]+d[1];
                    if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == 0 && !vis[nx][ny]) {
                        vis[nx][ny] = true;
                        q.add(new int[]{nx, ny});
                    }
                }
            }
            return false;
        };
        while (l <= r) {
            int m = l + (r-l)/2;
            if (canCross.test(m)) { ans = m; l = m+1; }
            else r = m-1;
        }
        return ans+1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
    fun latestDayToCross(row: Int, col: Int, cells: Array<IntArray>): Int {
        val dirs = arrayOf(intArrayOf(0,1), intArrayOf(1,0), intArrayOf(0,-1), intArrayOf(-1,0))
        fun canCross(day: Int): Boolean {
            val grid = Array(row) { IntArray(col) }
            for (i in 0..day) grid[cells[i][0]-1][cells[i][1]-1] = 1
            val vis = Array(row) { BooleanArray(col) }
            val q = ArrayDeque<Pair<Int,Int>>()
            for (j in 0 until col) if (grid[0][j] == 0) { q.add(0 to j); vis[0][j] = true }
            while (q.isNotEmpty()) {
                val (x, y) = q.removeFirst()
                if (x == row-1) return true
                for (d in dirs) {
                    val nx = x + d[0]; val ny = y + d[1]
                    if (nx in 0 until row && ny in 0 until col && grid[nx][ny] == 0 && !vis[nx][ny]) {
                        vis[nx][ny] = true
                        q.add(nx to ny)
                    }
                }
            }
            return false
        }
        var l = 0; var r = cells.size-1; var ans = 0
        while (l <= r) {
            val m = l + (r-l)/2
            if (canCross(m)) { ans = m; l = m+1 } else r = m-1
        }
        return ans+1
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution:
    def latestDayToCross(self, row: int, col: int, cells: list[list[int]]) -> int:
        from collections import deque
        dirs = [(0,1),(1,0),(0,-1),(-1,0)]
        def can_cross(day: int) -> bool:
            grid = [[0]*col for _ in range(row)]
            for i in range(day+1):
                r, c = cells[i][0]-1, cells[i][1]-1
                grid[r][c] = 1
            vis = [[False]*col for _ in range(row)]
            q = deque()
            for j in range(col):
                if grid[0][j] == 0:
                    q.append((0, j))
                    vis[0][j] = True
            while q:
                x, y = q.popleft()
                if x == row-1:
                    return True
                for dx, dy in dirs:
                    nx, ny = x+dx, y+dy
                    if 0 <= nx < row and 0 <= ny < col and grid[nx][ny] == 0 and not vis[nx][ny]:
                        vis[nx][ny] = True
                        q.append((nx, ny))
            return False
        l, r, ans = 0, len(cells)-1, 0
        while l <= r:
            m = l + (r-l)//2
            if can_cross(m):
                ans = m
                l = m+1
            else:
                r = m-1
        return ans+1
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

impl Solution {
    pub fn latest_day_to_cross(row: i32, col: i32, cells: Vec<Vec<i32>>) -> i32 {
        let row = row as usize;
        let col = col as usize;
        let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
        let can_cross = |day: usize| -> bool {
            let mut grid = vec![vec![0; col]; row];
            for i in 0..=day { grid[(cells[i][0]-1) as usize][(cells[i][1]-1) as usize] = 1; }
            let mut vis = vec![vec![false; col]; row];
            let mut q = std::collections::VecDeque::new();
            for j in 0..col { if grid[0][j] == 0 { q.push_back((0,j)); vis[0][j] = true; } }
            while let Some((x, y)) = q.pop_front() {
                if x == row-1 { return true; }
                for (dx, dy) in dirs.iter() {
                    let nx = x as i32 + dx;
                    let ny = y as i32 + dy;
                    if nx >= 0 && nx < row as i32 && ny >= 0 && ny < col as i32 {
                        let (nx, ny) = (nx as usize, ny as usize);
                        if grid[nx][ny] == 0 && !vis[nx][ny] {
                            vis[nx][ny] = true;
                            q.push_back((nx, ny));
                        }
                    }
                }
            }
            false
        };
        let (mut l, mut r, mut ans) = (0, cells.len()-1, 0);
        while l <= r {
            let m = l + (r-l)/2;
            if can_cross(m) { ans = m; l = m+1; } else { r = m-1; }
        }
        (ans+1) as i32
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
    latestDayToCross(row: number, col: number, cells: number[][]): number {
        const dirs = [[0,1],[1,0],[0,-1],[-1,0]];
        const canCross = (day: number): boolean => {
            const grid = Array.from({length: row}, () => Array(col).fill(0));
            for (let i = 0; i <= day; i++) grid[cells[i][0]-1][cells[i][1]-1] = 1;
            const vis = Array.from({length: row}, () => Array(col).fill(false));
            const q: [number, number][] = [];
            for (let j = 0; j < col; j++) if (grid[0][j] === 0) { q.push([0, j]); vis[0][j] = true; }
            while (q.length) {
                const [x, y] = q.shift()!;
                if (x === row-1) return true;
                for (const [dx, dy] of dirs) {
                    const nx = x+dx, ny = y+dy;
                    if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] === 0 && !vis[nx][ny]) {
                        vis[nx][ny] = true;
                        q.push([nx, ny]);
                    }
                }
            }
            return false;
        };
        let l = 0, r = cells.length-1, ans = 0;
        while (l <= r) {
            const m = l + ((r-l)>>1);
            if (canCross(m)) { ans = m; l = m+1; } else r = m-1;
        }
        return ans+1;
    }
}

Complexity

  • ⏰ Time complexity: O(row*col*log(row*col)), because for each binary search step (log(rowcol)), we do a BFS that can visit every cell (rowcol).
  • 🧺 Space complexity: O(row*col), for the grid and visited arrays used in BFS.