Problem

We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with a speed of 1 unit per second. Some of the ants move to the left , the other move to the right.

When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.

When an ant reaches one end of the plank at a time t, it falls out of the plank immediately.

Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right, return the moment when the last ant(s) fall out of the plank.

Examples

Example 1

1
2
3
4
5
6
7
8

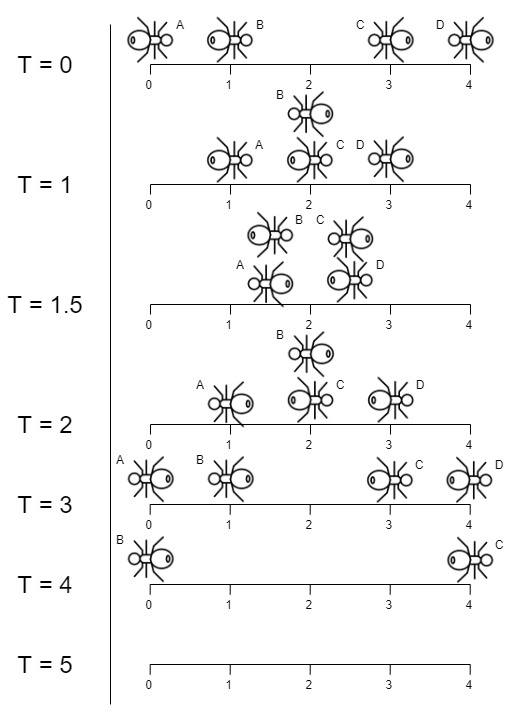
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).

Example 2

1
2
3

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3

1
2
3

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

Constraints

  • 1 <= n <= 10^4
  • 0 <= left.length <= n + 1
  • 0 <= left[i] <= n
  • 0 <= right.length <= n + 1
  • 0 <= right[i] <= n
  • 1 <= left.length + right.length <= n + 1
  • All values of left and right are unique, and each value can appear only in one of the two arrays.

Solution

Method 1 – Max Distance to Edge (Brainteaser)

Intuition

The direction change when ants meet does not affect the time they fall off, since swapping directions is equivalent to swapping identities. Thus, each ant will fall off at the same time as if it moved straight to the edge without any collisions.

Approach

  1. For ants moving left, the time to fall is their current position (distance to left edge).
  2. For ants moving right, the time to fall is n - position (distance to right edge).
  3. The answer is the maximum of all these times.

Code

1
2
3
4
5
6
7
8
9

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        int ans = 0;
        for (int x : left) ans = max(ans, x);
        for (int x : right) ans = max(ans, n - x);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func getLastMoment(n int, left []int, right []int) int {
    ans := 0
    for _, x := range left {
        if x > ans {
            ans = x
        }
    }
    for _, x := range right {
        if n-x > ans {
            ans = n-x
        }
    }
    return ans
}
1
2
3
4
5
6
7
8

class Solution {
    public int getLastMoment(int n, int[] left, int[] right) {
        int ans = 0;
        for (int x : left) ans = Math.max(ans, x);
        for (int x : right) ans = Math.max(ans, n - x);
        return ans;
    }
}
1
2
3
4
5
6
7
8

class Solution {
    fun getLastMoment(n: Int, left: IntArray, right: IntArray): Int {
        var ans = 0
        for (x in left) ans = maxOf(ans, x)
        for (x in right) ans = maxOf(ans, n - x)
        return ans
    }
}
1
2
3
4
5
6
7

def getLastMoment(n: int, left: list[int], right: list[int]) -> int:
    ans = 0
    for x in left:
        ans = max(ans, x)
    for x in right:
        ans = max(ans, n - x)
    return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

impl Solution {
    pub fn get_last_moment(n: i32, left: Vec<i32>, right: Vec<i32>) -> i32 {
        let mut ans = 0;
        for &x in &left {
            ans = ans.max(x);
        }
        for &x in &right {
            ans = ans.max(n - x);
        }
        ans
    }
}
1
2
3
4
5
6
7
8

class Solution {
    getLastMoment(n: number, left: number[], right: number[]): number {
        let ans = 0;
        for (const x of left) ans = Math.max(ans, x);
        for (const x of right) ans = Math.max(ans, n - x);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(L + R) – One pass through both arrays.
  • 🧺 Space complexity: O(1) – Only a few variables for computation