Problem

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.

A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Examples

Example 1:

1
2

Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]

Example 2:

1
2

Input: digits = ""
Output: []

Example 3:

1
2

Input: digits = "2"
Output: ["a","b","c"]

Solution

How do we solve this problem? Let’s quickly take our phone and look into the keypad. We will find –

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

0 --> {}
1 --> {}
2 --> {a,b,c}
3 --> {d,e,f}
4 --> {g,h,i}
5 --> {j,k,l}
6 --> {m,n,o}
7 --> {p,q,r,s}
8 --> {t,u,v}
9 --> {w,x,y,z}

Now if we press 2 there could be 3 possible values {a, b, c}. Then if we press 3 then the possible words would be all combination of 2 letters, one from 2–>{a, b, c} and other from 3->{d, e, f}. If we press down another number then the words formed will have first letter from 2-{a, b, c}, second number from 3->{d, e, f}, and 3rd letter from 4->{g, h, i}.

Does this look familiar? Yes, we solved this problem: List Combinations - Generate unique combinations from list selecting 1 element from each

Basically we run the algorithm with a list {L2, L3, L4} where

1
2
3

L2= {a, b, c}
L3= {d, e, f}
L4= {g, h, i}

So, given a sequence of n digits we will generate a list of lists using a precomputed map from digit to list of characters. Then we will call the permuteList.

Method 1 -DFS

This problem can be solves by a typical DFS algorithm. DFS problems are very similar and can be solved by using a simple recursion.

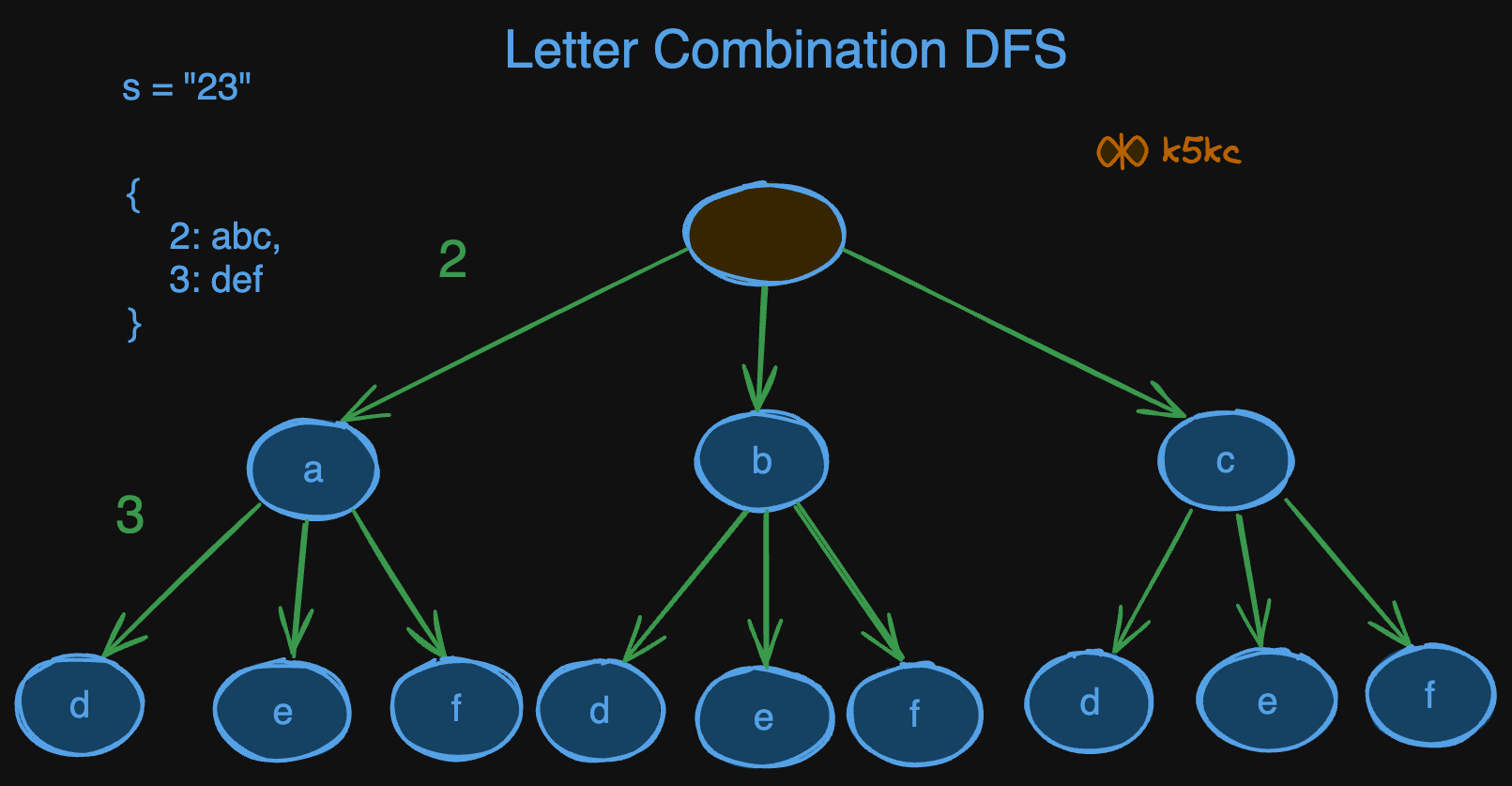
So, we will start with first index 0 in digits, then the next one, and so on.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

public List<String> letterCombinations(String digits) {
	HashMap<Integer, String> digitsToCharMap = new HashMap<Integer, String> ();
	digitsToCharMap.put(2, "abc");
	digitsToCharMap.put(3, "def");
	digitsToCharMap.put(4, "ghi");
	digitsToCharMap.put(5, "jkl");
	digitsToCharMap.put(6, "mno");
	digitsToCharMap.put(7, "pqrs");
	digitsToCharMap.put(8, "tuv");
	digitsToCharMap.put(9, "wxyz");
	digitsToCharMap.put(0, "");

	List<String> ans = new ArrayList<String> ();

	if (digits == null || digits.length() == 0)
		return result;

	String currStr = new String();
	backtrack(digits, 0, currStr, ans, digitsToCharMap);

	return ans;
}

public void backtrack(String digits, int i, String currStr, List<String> result, Map<Integer, String> digitsToCharMap) {
	if (digits.length() == currStr.size()) {
		result.add(currStr);
		return;
	}

	int currDigit = digits.charAt(i) - '0';
	for (char c: digitsToCharMap.get(currDigit).toCharArray()){
		backtrack(digits, i+1, currStr + c, result, digitsToCharMap);
	}
}
 
1
2
3
4
5
6

// array
String[] mapping = {
		"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"
};
// combination:
String candidates = mapping[digits.charAt(index) - '0'];
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public List<String> letterCombinations(String digits) {
	Map<Character, char[]> digitsToCharMap = new HashMap<Integer, String> ();
	digitsToCharMap.put(2, "abc".toCharArray());
	digitsToCharMap.put(3, "def".toCharArray());
	digitsToCharMap.put(4, "ghi".toCharArray());
	digitsToCharMap.put(5, "jkl".toCharArray());
	digitsToCharMap.put(6, "mno".toCharArray());
	digitsToCharMap.put(7, "pqrs".toCharArray());
	digitsToCharMap.put(8, "tuv".toCharArray());
	digitsToCharMap.put(9, "wxyz".toCharArray());
	digitsToCharMap.put(0, "".toCharArray());

	ArrayList<String> result = new ArrayList<String> ();

	if (digits == null || digits.length() == 0)
		return result;

	StringBuilder currStr = new StringBuilder();
	backtrack(digits, 0, currStr, result, digitsToCharMap);

	return result;
}

public void backtrack(String digits, int i, StringBuilder currStr, List<String> result, Map<Character, char[]> digitsToCharMap) {
	if (digits.length() == currStr.size()) {
		result.add(currStr.toString());
		return;
	}

	int currDigit = digits.charAt(i) - '0';
	for (char c: digitsToCharMap.get(currDigit).toCharArray()){
		backtrack(digits, i+1, currStr.append(c), result, digitsToCharMap);
		currStr.deleteCharAt(sb.length() - 1);
	}
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52


public List<String> letterCombinations(String digits) {
	HashMap<Character, char[] > dict = new HashMap<Character, char[] > ();
	dict.put('2', new char[] {
		'a', 'b', 'c'
	});
	dict.put('3', new char[] {
		'd', 'e', 'f'
	});
	dict.put('4', new char[] {
		'g', 'h', 'i'
	});
	dict.put('5', new char[] {
		'j', 'k', 'l'
	});
	dict.put('6', new char[] {
		'm', 'n', 'o'
	});
	dict.put('7', new char[] {
		'p', 'q', 'r', 's'
	});
	dict.put('8', new char[] {
		't', 'u', 'v'
	});
	dict.put('9', new char[] {
		'w', 'x', 'y', 'z'
	});

	List<String> result = new ArrayList<String> ();
	if (digits == null || digits.length() == 0) {
		return result;
	}

	char[] arr = new char[digits.length()];
	helper(digits, 0, dict, result, arr);

	return result;
}

private void helper(String digits, int index, HashMap<Character, char[] > dict, List<String> result, char[] arr) {
	if (index == digits.length()) {
		result.add(new String(arr));
		return;
	}

	char number = digits.charAt(index);
	char[] candidates = dict.get(number);
	for (int i = 0; i<candidates.length; i++) {
		arr[index] = candidates[i];
		helper(digits, index + 1, dict, result, arr);
	}
}

Complexity

  • ⏰ Time complexity: O(n*4^n), As, we loop over n chars in string digits, so it will be n* X. X will come from cases for eg. 9, it may map to wxyz i.e. 4 chars, time complexity is 4^n, hence overall time complexity.
  • 🧺 Space complexity: O(n) assuming recursive stack.