problemmediumalgorithmsleetcode-558leetcode 558leetcode558

Logical OR of Two Binary Grids Represented as Quad-Trees

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

A Binary Matrix is a matrix in which all the elements are either 0 or 1.

Given quadTree1 and quadTree2. quadTree1 represents a n * n binary matrix and quadTree2 represents another n * n binary matrix.

Return a Quad-Tree representing the n * n binary matrix which is the result of logical bitwise OR of the two binary matrixes represented by quadTree1 and quadTree2.

Notice that you can assign the value of a node to True or False when isLeaf is False , and both are accepted in the answer.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

  • val: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
  • isLeaf: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
  public boolean val;
  public boolean isLeaf;
  public Node topLeft;
  public Node topRight;
  public Node bottomLeft;
  public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

  1. If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
  2. If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
  3. Recurse for each of the children with the proper sub-grid.

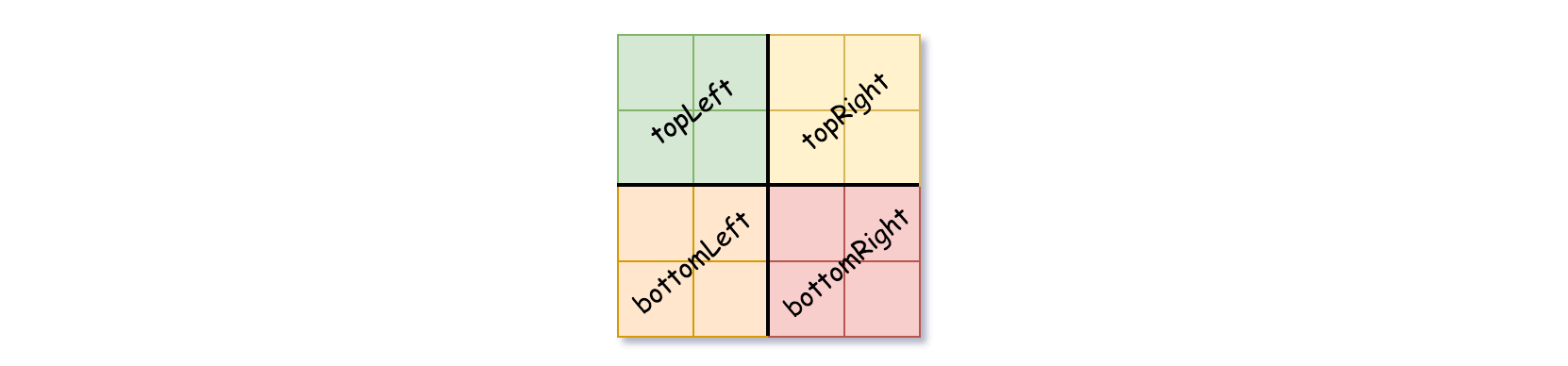
If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

The input/output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

Examples

Example 1


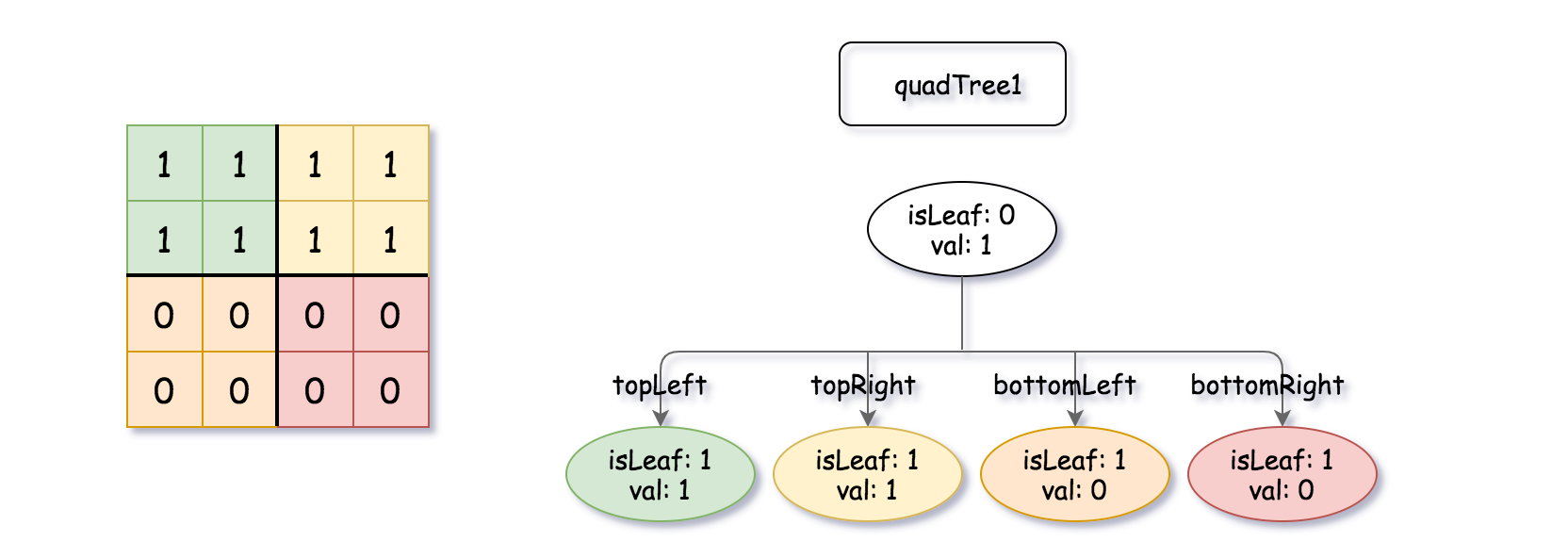
![](https://assets.leetcode.com/uploads/2020/02/11/qt1.png)
![](https://assets.leetcode.com/uploads/2020/02/11/qt2.png)

Input: quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
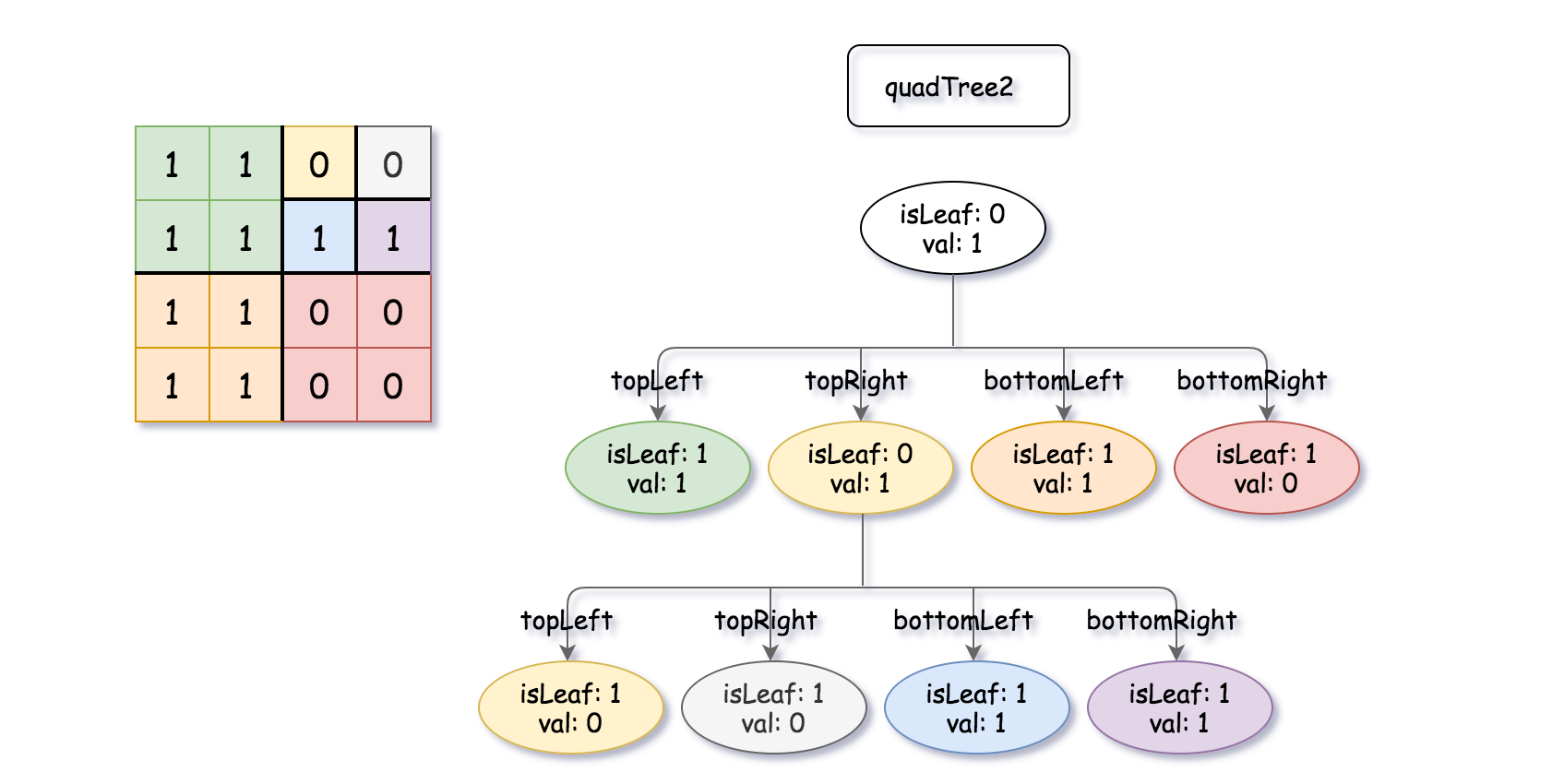
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
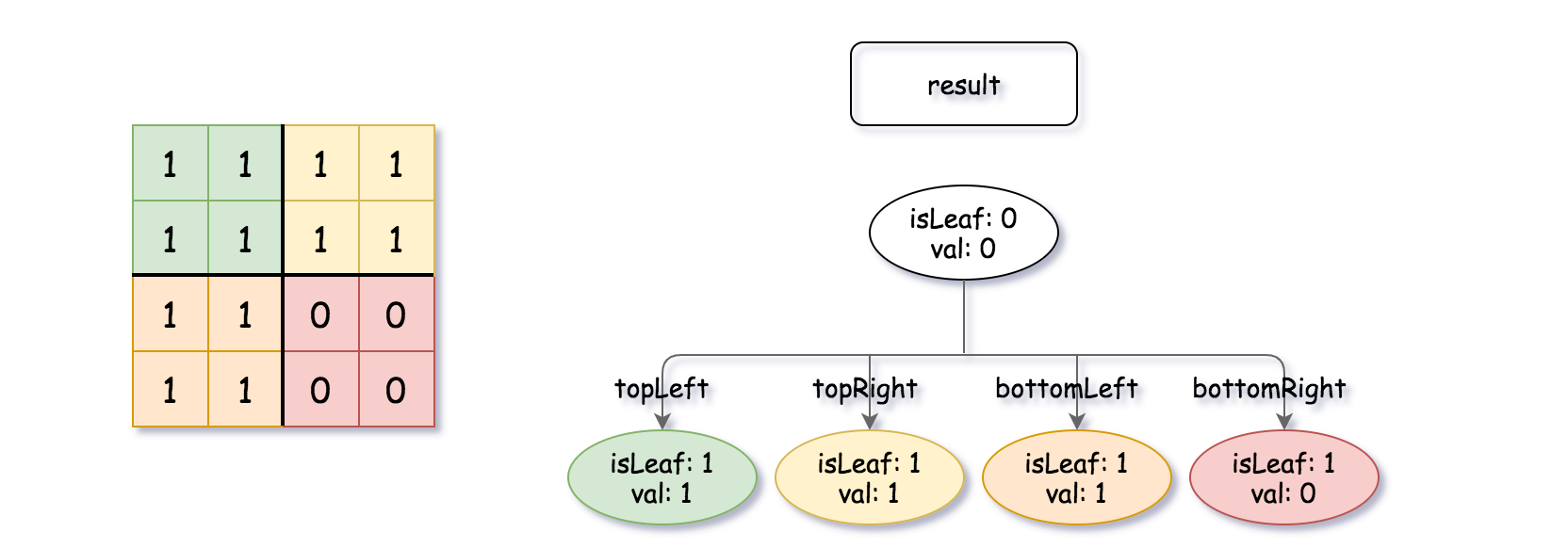
Output: [[0,0],[1,1],[1,1],[1,1],[1,0]]
Explanation: quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.
![](https://assets.leetcode.com/uploads/2020/02/11/qtr.png)

Example 2

Input: quadTree1 = [[1,0]], quadTree2 = [[1,0]]
Output: [[1,0]]
Explanation: Each tree represents a binary matrix of size 1*1. Each matrix contains only zero.
The resulting matrix is of size 1*1 with also zero.

Constraints

  • quadTree1 and quadTree2 are both valid Quad-Trees each representing a n * n grid.
  • n == 2x where 0 <= x <= 9.

Solution

Method 1 – Recursive Divide and Conquer (1)

Intuition

The logical OR of two quad-trees can be computed recursively: if either node is a leaf and its value is True, the result is a leaf with value True. If both are leaves, the result is a leaf with the OR of their values. Otherwise, recursively OR the four children.

Approach

  1. If either node is a leaf and its value is True, return a leaf node with value True.
  2. If either node is a leaf and its value is False, return the other node.
  3. Otherwise, recursively OR the four children (topLeft, topRight, bottomLeft, bottomRight).
  4. If all four children are leaves and have the same value, merge them into a single leaf node.
  5. Otherwise, return a node with these four children.

Code

C++
class Solution {
public:
    Node* intersect(Node* n1, Node* n2) {
        if (n1->isLeaf) return n1->val ? n1 : n2;
        if (n2->isLeaf) return n2->val ? n2 : n1;
        Node* tl = intersect(n1->topLeft, n2->topLeft);
        Node* tr = intersect(n1->topRight, n2->topRight);
        Node* bl = intersect(n1->bottomLeft, n2->bottomLeft);
        Node* br = intersect(n1->bottomRight, n2->bottomRight);
        if (tl->isLeaf && tr->isLeaf && bl->isLeaf && br->isLeaf &&
            tl->val == tr->val && tr->val == bl->val && bl->val == br->val) {
            return new Node(tl->val, true);
        }
        return new Node(false, false, tl, tr, bl, br);
    }
};
Go
func intersect(n1, n2 *Node) *Node {
    if n1.IsLeaf {
        if n1.Val { return n1 }
        return n2
    }
    if n2.IsLeaf {
        if n2.Val { return n2 }
        return n1
    }
    tl := intersect(n1.TopLeft, n2.TopLeft)
    tr := intersect(n1.TopRight, n2.TopRight)
    bl := intersect(n1.BottomLeft, n2.BottomLeft)
    br := intersect(n1.BottomRight, n2.BottomRight)
    if tl.IsLeaf && tr.IsLeaf && bl.IsLeaf && br.IsLeaf &&
        tl.Val == tr.Val && tr.Val == bl.Val && bl.Val == br.Val {
        return &Node{Val: tl.Val, IsLeaf: true}
    }
    return &Node{IsLeaf: false, TopLeft: tl, TopRight: tr, BottomLeft: bl, BottomRight: br}
}
Java
class Solution {
    public Node intersect(Node n1, Node n2) {
        if (n1.isLeaf) return n1.val ? n1 : n2;
        if (n2.isLeaf) return n2.val ? n2 : n1;
        Node tl = intersect(n1.topLeft, n2.topLeft);
        Node tr = intersect(n1.topRight, n2.topRight);
        Node bl = intersect(n1.bottomLeft, n2.bottomLeft);
        Node br = intersect(n1.bottomRight, n2.bottomRight);
        if (tl.isLeaf && tr.isLeaf && bl.isLeaf && br.isLeaf &&
            tl.val == tr.val && tr.val == bl.val && bl.val == br.val) {
            return new Node(tl.val, true);
        }
        return new Node(false, false, tl, tr, bl, br);
    }
}
Kotlin
class Solution {
    fun intersect(n1: Node?, n2: Node?): Node? {
        if (n1!!.isLeaf) return if (n1.`val`) n1 else n2
        if (n2!!.isLeaf) return if (n2.`val`) n2 else n1
        val tl = intersect(n1.topLeft, n2.topLeft)
        val tr = intersect(n1.topRight, n2.topRight)
        val bl = intersect(n1.bottomLeft, n2.bottomLeft)
        val br = intersect(n1.bottomRight, n2.bottomRight)
        if (tl!!.isLeaf && tr!!.isLeaf && bl!!.isLeaf && br!!.isLeaf &&
            tl.`val` == tr.`val` && tr.`val` == bl.`val` && bl.`val` == br.`val`) {
            return Node(tl.`val`, true)
        }
        return Node(false, false, tl, tr, bl, br)
    }
}
Python
class Solution:
    def intersect(self, n1: 'Node', n2: 'Node') -> 'Node':
        if n1.isLeaf:
            return n1 if n1.val else n2
        if n2.isLeaf:
            return n2 if n2.val else n1
        tl = self.intersect(n1.topLeft, n2.topLeft)
        tr = self.intersect(n1.topRight, n2.topRight)
        bl = self.intersect(n1.bottomLeft, n2.bottomLeft)
        br = self.intersect(n1.bottomRight, n2.bottomRight)
        if tl.isLeaf and tr.isLeaf and bl.isLeaf and br.isLeaf and \
           tl.val == tr.val == bl.val == br.val:
            return Node(tl.val, True)
        return Node(False, False, tl, tr, bl, br)
Rust
impl Solution {
    pub fn intersect(n1: Option<Rc<RefCell<Node>>>, n2: Option<Rc<RefCell<Node>>>) -> Option<Rc<RefCell<Node>>> {
        use std::rc::Rc;
        use std::cell::RefCell;
        let (n1, n2) = (n1.unwrap(), n2.unwrap());
        let (n1, n2) = (n1.borrow(), n2.borrow());
        if n1.isLeaf {
            if n1.val {
                return Some(Rc::new(RefCell::new(Node::new(n1.val, true, None, None, None, None))));
            } else {
                return Some(Rc::new(RefCell::new(Node::new(n2.val, n2.isLeaf, n2.topLeft.clone(), n2.topRight.clone(), n2.bottomLeft.clone(), n2.bottomRight.clone()))));
            }
        }
        if n2.isLeaf {
            if n2.val {
                return Some(Rc::new(RefCell::new(Node::new(n2.val, true, None, None, None, None))));
            } else {
                return Some(Rc::new(RefCell::new(Node::new(n1.val, n1.isLeaf, n1.topLeft.clone(), n1.topRight.clone(), n1.bottomLeft.clone(), n1.bottomRight.clone()))));
            }
        }
        let tl = Solution::intersect(n1.topLeft.clone(), n2.topLeft.clone());
        let tr = Solution::intersect(n1.topRight.clone(), n2.topRight.clone());
        let bl = Solution::intersect(n1.bottomLeft.clone(), n2.bottomLeft.clone());
        let br = Solution::intersect(n1.bottomRight.clone(), n2.bottomRight.clone());
        let all_leaf = |n: &Option<Rc<RefCell<Node>>>| n.as_ref().unwrap().borrow().isLeaf;
        let all_val = |n: &Option<Rc<RefCell<Node>>>| n.as_ref().unwrap().borrow().val;
        if all_leaf(&tl) && all_leaf(&tr) && all_leaf(&bl) && all_leaf(&br) &&
            all_val(&tl) == all_val(&tr) && all_val(&tr) == all_val(&bl) && all_val(&bl) == all_val(&br) {
            return Some(Rc::new(RefCell::new(Node::new(all_val(&tl), true, None, None, None, None))));
        }
        Some(Rc::new(RefCell::new(Node::new(false, false, tl, tr, bl, br))))
    }
}
TypeScript
class Solution {
    intersect(n1: Node, n2: Node): Node {
        if (n1.isLeaf) return n1.val ? n1 : n2;
        if (n2.isLeaf) return n2.val ? n2 : n1;
        const tl = this.intersect(n1.topLeft, n2.topLeft);
        const tr = this.intersect(n1.topRight, n2.topRight);
        const bl = this.intersect(n1.bottomLeft, n2.bottomLeft);
        const br = this.intersect(n1.bottomRight, n2.bottomRight);
        if (tl.isLeaf && tr.isLeaf && bl.isLeaf && br.isLeaf &&
            tl.val === tr.val && tr.val === bl.val && bl.val === br.val) {
            return new Node(tl.val, true);
        }
        return new Node(false, false, tl, tr, bl, br);
    }
}

Complexity

  • ⏰ Time complexity: O(N), where N is the number of nodes in the quad-tree. Each node is visited once.
  • 🧺 Space complexity: O(H), where H is the height of the tree, due to recursion stack.

Comments