Longest Common Subsequence LCS 1 - Get Length

Problem

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

• For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

Examples

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Follow up

Can you get the longest common subsequence as well? [Longest Common Subsequence LCS 2 - Get Subsequence](longest-common-subsequence-lcs-2-get-subsequence)

Solution

For arbitrary inputs, it is NP-hard. For constant inputs, DP gives the solution in polynomial time ex: O(n^k). Also, there can be more than one LCSs and the solution for that is exponential time ex: O(k^n).

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/84bHfaJf6RY" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Recursion

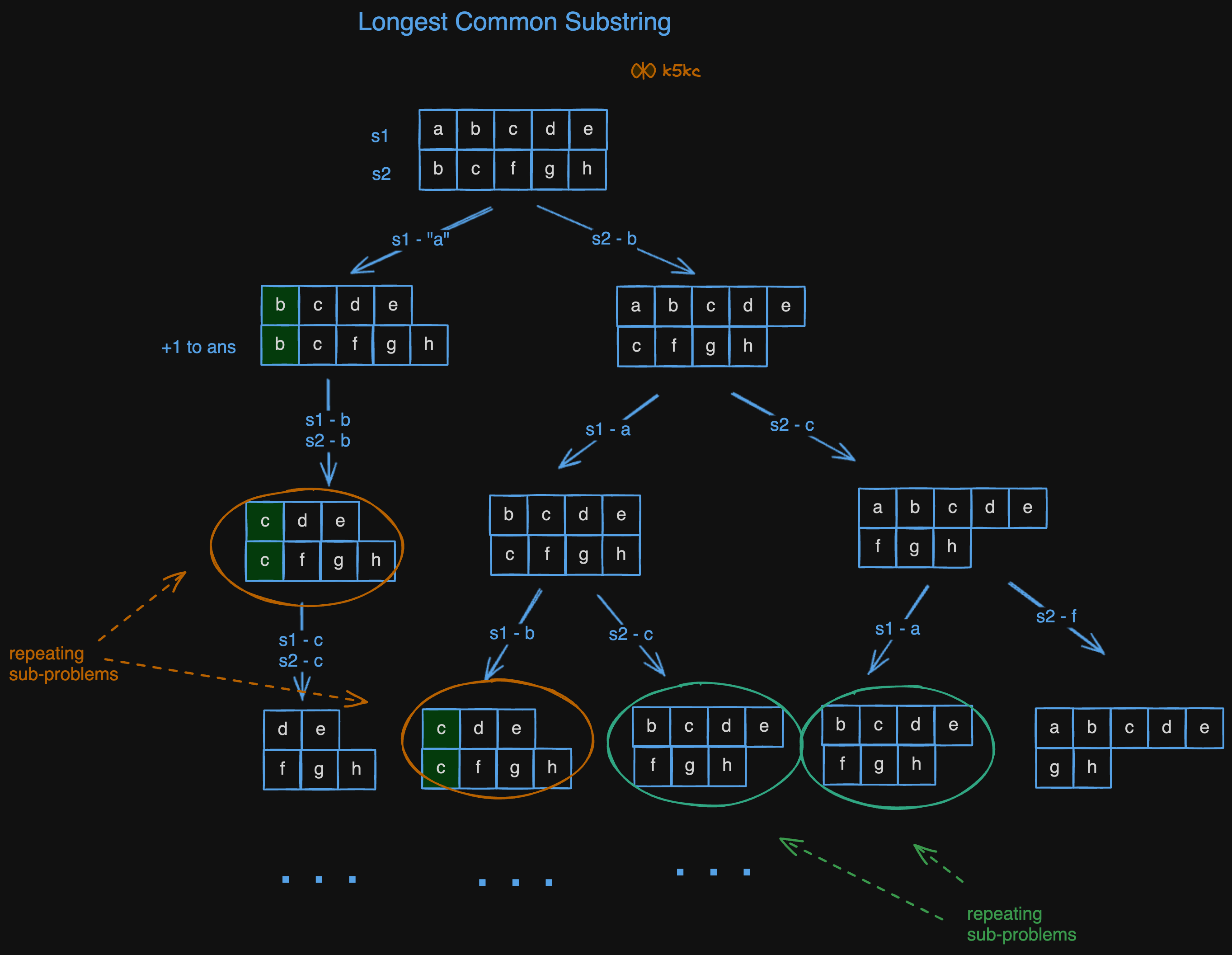
The LCS length is found by iteratively comparing characters from start, adding 1 for matches and recursively comparing remaining subsequences after character removal for mismatches.

Code

Java

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        return helper(text1, text2, 0, 0);
    }
    
    private int helper(String text1, String text2, int i, int j) {
        if (i == text1.length() || j == text2.length()) {
	        return 0;
        }
            
        if (text1.charAt(i) == text2.charAt(j)) {
	        return 1 + helper(text1, text2, i + 1, j + 1);
        }
        else {
            return Math.max(
                helper(text1, text2, i + 1, j),
                helper(text1, text2, i, j + 1)
            );
        }
    }
}

Python

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        return self.helper(text1, text2, 0, 0)
    
    def helper(self, text1: str, text2: str, i: int, j: int) -> int:
        # Base case: if we've gone beyond the end of either string
        if i == len(text1) or j == len(text2):
            return 0
        
        # If characters match, move diagonally in both strings
        if text1[i] == text2[j]:
            return 1 + self.helper(text1, text2, i + 1, j + 1)
        else:
            # Otherwise, take the max of skipping one character in either string
            return max(
                self.helper(text1, text2, i + 1, j),
                self.helper(text1, text2, i, j + 1)
            )

Complexity

• ⏰ Time complexity: O(2^(m*n))
• 🧺 Space complexity: O(m*n)

Method 2 - Top Down DP

As we see in the diagram above, that we have overlapping subproblems. We might use memoization to overcome overlapping subproblems. Since there are two changing values, i.e. i and j in the recursive function longestCommonSubsequence, we might apply a two-dimensional array as a cache.

Code

Java

Note that we are are using Integer[m][n] and not int[m][n], otherwise we get TLE. The reason is if we use 0 instead of null, then we go into the calculations again and again, and even 0 is a valid output. If we want to use int[][] array, then better thing is to fill it with -1 as default value, and it should work out as well.

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        return helper(text1, text2, 0, 0, new Integer[text1.length()][text2.length()]);
    }
    
    private int longestCommonSubsequence(String text1, String text2, int i, int j, Integer[][] cache) {
        if (i == text1.length() || j == text2.length()) {
	        return 0;
        }
        
        if (cache[i][j] != null) {
	        return cache[i][j];
        }
            
        if (text1.charAt(i) == text2.charAt(j)) {
	        return cache[i][j] = 1 + helper(text1, text2, i + 1, j + 1, cache);
        }
        else {
            return cache[i][j] = Math.max(
                helper(text1, text2, i + 1, j, cache),
                helper(text1, text2, i, j + 1, cache)
            );
        }
    }
}

Python

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        cache = [[None] * len(text2) for _ in range(len(text1))]
        return self.helper(text1, text2, 0, 0, cache)

    def helper(self, text1: str, text2: str, i: int, j: int, cache: list) -> int:
        if i == len(text1) or j == len(text2):
            return 0

        if cache[i][j] is not None:
            return cache[i][j]

        if text1[i] == text2[j]:
            cache[i][j] = 1 + self.helper(text1, text2, i + 1, j + 1, cache)
        else:
            cache[i][j] = max(
                self.helper(text1, text2, i + 1, j, cache),
                self.helper(text1, text2, i, j + 1, cache)
            )

        return cache[i][j]

Complexity

• ⏰ Time complexity: O(m*n)
• 🧺 Space complexity: O(m*n)

Method 3 - Bottom Up DP

We will solve it in bottom-up DP and store the solution of the sub problems in a solution array.

Let dp[i+1][j+1] be the length of the longest common subsequence of string text1 & text2, when text1[i] and text2[j] are compared to each other. (0<=i<=m-1, 0<=j<=n-1)

When i OR j are 0, then we have empty string. That means the common length is 0.

LCS[i, j] = 0                             for i = 0 or j = 0
          = LCS[i-1,j-1] + 1              for x[i] = y[j]
          = max(LCS[i-1,j],LCS[i, j-1])   for x[i] != y[j]

We can also fill the array from end, like we did in recursion solution. But we are coding from the start.

Code

Java

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
		int m = text1.length();
		int n = text2.length();
		int[][] dp = new int[m + 1][n + 1];
		// no need to start from i and j = 0, as default value is 0
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
	                dp[i][j] = 1 + dp[i - 1][j - 1];
                }
                else {
	                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

Python

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        
        # Create a 2D dp array with (m+1) x (n+1) filled with 0
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        
        # Fill the DP table
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:  # Match case
                    dp[i][j] = 1 + dp[i - 1][j - 1]
                else:  # No match; take the max from left or top cell
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        
        # The result is stored in the bottom-right cell
        return dp[m][n]

Complexity

• ⏰ Time complexity: O(m*n)
• 🧺 Space complexity: O(m*n)

Dry Run

This is how the DP array will look like for string "abcde" and "ace":

	Ø	a	c	e
Ø	0	0	0	0
a	0	1	1	1
b	0	1	1	1
c	0	1	2	2
d	0	1	2	2
e	0	1	2	3

When filling in we have 2 cases

• if (text1.charAt(i) == text2.charAt(j)), then we do 1 + dp[i-1][j-1]:

For e.g. filing in i = 1, j = 1 (for char a in text1 and text2), marked in green, and prev value in orange:

• if (text1.charAt(i) != text2.charAt(j)) then we filling using Math.max(dp[i - 1][j], dp[i][j - 1])

For eg. i = 1, j = 2 (marked green), it takes marked in orange.:

Method 4 - Space Optimized Bottom up DP

The key observation in previous approach is that each iteration only needs previous row values. We can leverage this by using just two rows (dp[2][n+1]) instead of the entire table (dp[m+1][n+1]), reducing memory usage significantly. See the updated implementation below.

1. Instead of maintaining a table of size (m+1) x (n+1), we reduce the space to 2 rows of size (n+1).
2. These 2 rows alternate between representing the "current row" and "previous row":
   • For the current DP row, use dp[i % 2].
   • For the previous DP row, use dp[(i-1) % 2].

Approach

1. Space Reduction:
   • Instead of creating a 2D dp table of size (m+1) x (n+1), create a dp array of size 2 x (n+1).
   • These two rows are alternated during the computation.
2. Row Alternation:
   • For each character in text1 (indexed by i), compute the results row by row.
   • Use i % 2 for the current row and (i-1) % 2 for the previous row. This alternation allows us to reuse space while maintaining correctness.
3. Character Match:
   • If text1[i-1] == text2[j-1], update dp[i % 2][j] = dp[(i-1) % 2][j-1] + 1. Add 1 to the diagonal value since this character contributes to the LCS.
4. Character Mismatch:
   • If text1[i-1] != text2[j-1], take the maximum of the two possibilities:
     • dp[(i-1) % 2][j] (skipping the current character in text1).
     • dp[i % 2][j-1] (skipping the current character in text2).
   • Update dp[i % 2][j] to be the maximum of these values.
5. Final Result:
   • After iterating through both strings, the LCS length is stored in dp[m % 2][n].

Code

Java

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
		int m = text1.length();
		int n = text2.length();
		int[][] dp = new int[2][n + 1];
		// no need to start from i and j = 0, as default value is 0
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
	                dp[i % 2][j] = 1 + dp[(i - 1) % 2][j - 1];
                }
                else {
	                dp[i % 2][j] = Math.max(dp[(i - 1) % 2][j], dp[i % 2][j - 1]);
                }
            }
        }
        return dp[m%2][n];
    }
}

Complexity

• ⏰ Time complexity: O(m*n)
• 🧺 Space complexity: O(2*n) = O(n)