Problem

Given two sequences, return the longest subsequence present in both of them.

Examples

Example 1:

1
2
3

Input: text1 = "abcde", text2 = "ace" 
Output: "ace"
Explanation: The longest common subsequence is "ace".

Example 2:

1
2
3

Input: text1 = "abc", text2 = "abc"
Output: "abc"
Explanation: The longest common subsequence is "abc".

Example 3:

1
2
3

Input: text1 = "abc", text2 = "def"
Output: ""
Explanation: There is no such common subsequence.

This is a follow up of Longest Common Subsequence LCS 1 - Get Length.

Solution

Method 1 - Using DP array to generate the subsequence

Lets look at the dp array again, say for string text1 = abcde, text2 = ace and LCS = ace:

Ø a c e
Ø 0 0 0 0
a 0 1 1 1
b 0 1 1 1
c 0 1 2 2
d 0 1 2 2
e 0 1 2 3
Now, lets look at it closely:

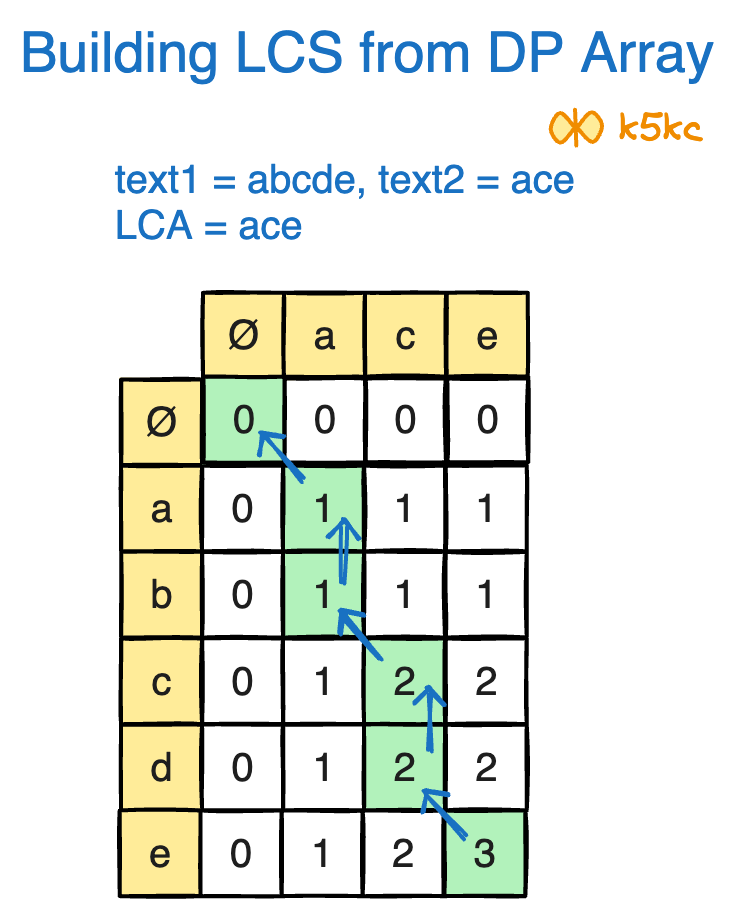
We begin traceback from the bottom-right corner, marking cells that contribute to the LCS and indicating diagonal movements (matching characters) for reconstruction.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

public String longestCommonSubsequence(String text1, String text2) {
	int m = text1.length();
	int n = text2.length();
	
	int[][] dp = new int[m + 1][n + 1];

	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
				dp[i][j] = 1 + dp[i - 1][j - 1];
			} else {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}

	// No return in the loop, calculate LCS length first
	int idx = dp[m][n];

	// Handle the case where there's no LCS (idx = 0)
	if (idx == 0) {
		return "";
	}

	char[] lcs = new char[idx];
	int i = m;
	int j = n;

	while (i > 0 && j > 0) {
		// If current character in text1 and text2 are same,
		// then current character is part of LCS
		if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
			// Put current character in result
			lcs[idx - 1] = text1.charAt(i - 1);
			i--;
			j--;
			idx--;
		}

		// If not same, then find the larger of two and
		// go in the direction of larger value
		else if (dp[i - 1][j] > dp[i][j - 1]) {
			i--;
		}
		else {
			j--;
		}
	}

	return new String(lcs);
}

Complexity

  • ⏰ Time complexity: O(m*n)
  • 🧺 Space complexity: O(m*n)