Longest Special Path
Problem
You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1, represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui and
vi with length lengthi. You are also given an integer array nums, where
nums[i] represents the value at node i.
A special path is defined as a downward path from an ancestor node to a descendant node such that all the values of the nodes in that path are unique.
Note that a path may start and end at the same node.
Return an array result of size 2, where result[0] is the length of the
longest special path, and result[1] is the minimum number of nodes in all possible longest special paths.
Examples
Example 1
Input: edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums =
[2,1,2,1,3,1]
Output: [6,2]
Explanation:
#### In the image below, nodes are colored by their corresponding values in
`nums`
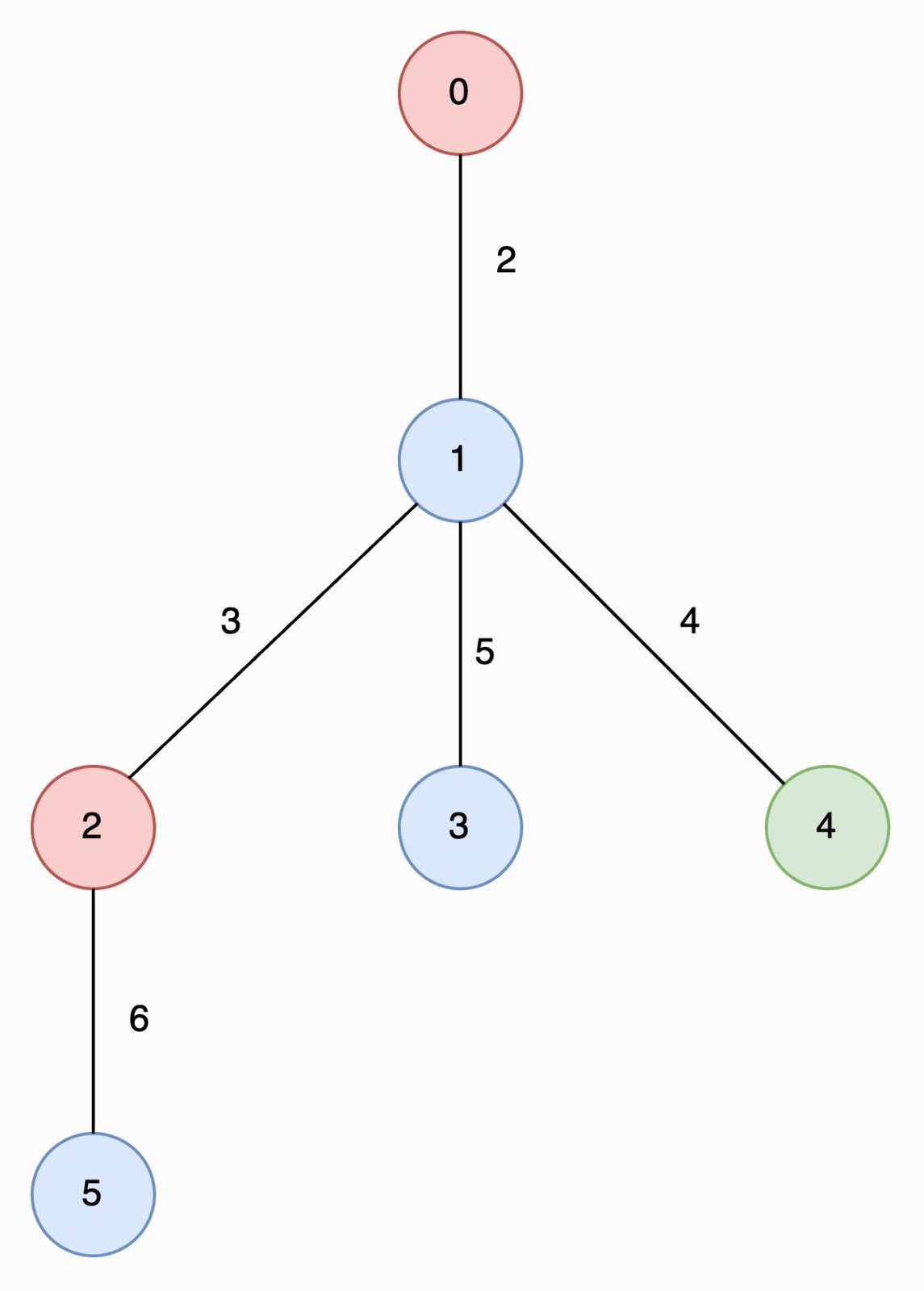
The longest special paths are `2 -> 5` and `0 -> 1 -> 4`, both having a length
of 6. The minimum number of nodes across all longest special paths is 2.
Example 2
Input: edges = [[1,0,8]], nums = [2,2]
Output: [0,1]
Explanation:
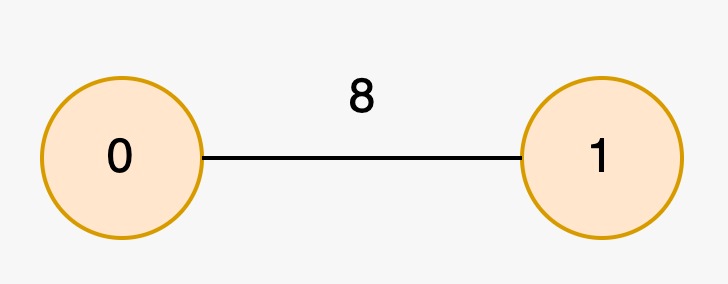
The longest special paths are `0` and `1`, both having a length of 0. The
minimum number of nodes across all longest special paths is 1.
Constraints
2 <= n <= 5 * 10^4edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= lengthi <= 10^3nums.length == n0 <= nums[i] <= 5 * 10^4- The input is generated such that
edgesrepresents a valid tree.
Solution
Method 1 – DFS with Backtracking and HashSet
Intuition
We need to find the longest downward path in a tree where all node values are unique. We use DFS to explore all paths, keeping track of visited values with a set. For each node, we try all children, backtracking as needed, and update the answer if a longer path is found. For ties in length, we track the minimum number of nodes.
Approach
- Build the tree as an adjacency list from the edges.
- For each node, perform DFS:
- Track the set of values in the current path.
- Track the current path length and total edge length.
- For each child, if its value is not in the set, continue DFS.
- Backtrack after visiting each child.
- For each node, start DFS and update the global answer if a longer or equally long path with fewer nodes is found.
- Return the maximum path length and minimum number of nodes for that length.
Code
C++
class Solution {
public:
vector<int> longestSpecialPath(vector<vector<int>>& edges, vector<int>& nums) {
int n = nums.size();
vector<vector<pair<int,int>>> g(n);
for (auto& e : edges) {
g[e[0]].push_back({e[1], e[2]});
g[e[1]].push_back({e[0], e[2]});
}
int maxLen = 0, minNodes = n+1;
function<void(int,int,set<int>&,int,int)> dfs = [&](int u, int p, set<int>& st, int len, int nodes) {
if (len > maxLen || (len == maxLen && nodes < minNodes)) {
maxLen = len;
minNodes = nodes;
}
for (auto& [v, w] : g[u]) {
if (v == p || st.count(nums[v])) continue;
st.insert(nums[v]);
dfs(v, u, st, len + w, nodes + 1);
st.erase(nums[v]);
}
};
for (int i = 0; i < n; ++i) {
set<int> st = {nums[i]};
dfs(i, -1, st, 0, 1);
}
return {maxLen, minNodes};
}
};
Go
func longestSpecialPath(edges [][]int, nums []int) []int {
n := len(nums)
g := make([][][2]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
}
maxLen, minNodes := 0, n+1
var dfs func(u, p int, st map[int]struct{}, length, nodes int)
dfs = func(u, p int, st map[int]struct{}, length, nodes int) {
if length > maxLen || (length == maxLen && nodes < minNodes) {
maxLen = length
minNodes = nodes
}
for _, vw := range g[u] {
v, w := vw[0], vw[1]
if v == p {
continue
}
if _, ok := st[nums[v]]; ok {
continue
}
st[nums[v]] = struct{}{}
dfs(v, u, st, length+w, nodes+1)
delete(st, nums[v])
}
}
for i := 0; i < n; i++ {
st := map[int]struct{}{nums[i]: {}}
dfs(i, -1, st, 0, 1)
}
return []int{maxLen, minNodes}
}
Java
class Solution {
public int[] longestSpecialPath(int[][] edges, int[] nums) {
int n = nums.length;
List<int[]>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(new int[]{e[1], e[2]});
g[e[1]].add(new int[]{e[0], e[2]});
}
int[] ans = new int[]{0, n+1};
Set<Integer> st = new HashSet<>();
dfs(0, -1, st, 0, 1, g, nums, ans);
for (int i = 1; i < n; i++) {
st.clear();
dfs(i, -1, st, 0, 1, g, nums, ans);
}
return ans;
}
void dfs(int u, int p, Set<Integer> st, int len, int nodes, List<int[]>[] g, int[] nums, int[] ans) {
st.add(nums[u]);
if (len > ans[0] || (len == ans[0] && nodes < ans[1])) {
ans[0] = len;
ans[1] = nodes;
}
for (int[] vw : g[u]) {
int v = vw[0], w = vw[1];
if (v == p || st.contains(nums[v])) continue;
dfs(v, u, st, len + w, nodes + 1, g, nums, ans);
st.remove(nums[v]);
}
}
}
Kotlin
class Solution {
fun longestSpecialPath(edges: Array<IntArray>, nums: IntArray): IntArray {
val n = nums.size
val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (e in edges) {
g[e[0]].add(Pair(e[1], e[2]))
g[e[1]].add(Pair(e[0], e[2]))
}
var maxLen = 0
var minNodes = n+1
fun dfs(u: Int, p: Int, st: MutableSet<Int>, len: Int, nodes: Int) {
if (len > maxLen || (len == maxLen && nodes < minNodes)) {
maxLen = len
minNodes = nodes
}
for ((v, w) in g[u]) {
if (v == p || st.contains(nums[v])) continue
st.add(nums[v])
dfs(v, u, st, len + w, nodes + 1)
st.remove(nums[v])
}
}
for (i in 0 until n) {
val st = mutableSetOf(nums[i])
dfs(i, -1, st, 0, 1)
}
return intArrayOf(maxLen, minNodes)
}
}
Python
class Solution:
def longestSpecialPath(self, edges: list[list[int]], nums: list[int]) -> list[int]:
from collections import defaultdict
n = len(nums)
g = defaultdict(list)
for u, v, w in edges:
g[u].append((v, w))
g[v].append((u, w))
max_len, min_nodes = 0, n+1
def dfs(u: int, p: int, st: set[int], length: int, nodes: int):
nonlocal max_len, min_nodes
if length > max_len or (length == max_len and nodes < min_nodes):
max_len = length
min_nodes = nodes
for v, w in g[u]:
if v == p or nums[v] in st:
continue
st.add(nums[v])
dfs(v, u, st, length + w, nodes + 1)
st.remove(nums[v])
for i in range(n):
dfs(i, -1, {nums[i]}, 0, 1)
return [max_len, min_nodes]
Rust
impl Solution {
pub fn longest_special_path(edges: Vec<Vec<i32>>, nums: Vec<i32>) -> Vec<i32> {
use std::collections::{HashSet, HashMap};
let n = nums.len();
let mut g = vec![vec![]; n];
for e in edges.iter() {
g[e[0] as usize].push((e[1] as usize, e[2]));
g[e[1] as usize].push((e[0] as usize, e[2]));
}
let mut max_len = 0;
let mut min_nodes = n as i32 + 1;
fn dfs(u: usize, p: i32, st: &mut HashSet<i32>, len: i32, nodes: i32, g: &Vec<Vec<(usize, i32)>>, nums: &Vec<i32>, max_len: &mut i32, min_nodes: &mut i32) {
if len > *max_len || (len == *max_len && nodes < *min_nodes) {
*max_len = len;
*min_nodes = nodes;
}
for &(v, w) in &g[u] {
if v as i32 == p || st.contains(&nums[v]) { continue; }
st.insert(nums[v]);
dfs(v, u as i32, st, len + w, nodes + 1, g, nums, max_len, min_nodes);
st.remove(&nums[v]);
}
}
for i in 0..n {
let mut st = HashSet::new();
st.insert(nums[i]);
dfs(i, -1, &mut st, 0, 1, &g, &nums, &mut max_len, &mut min_nodes);
}
vec![max_len, min_nodes]
}
}
TypeScript
class Solution {
longestSpecialPath(edges: number[][], nums: number[]): number[] {
const n = nums.length;
const g: [number, number][][] = Array.from({length: n}, () => []);
for (const [u, v, w] of edges) {
g[u].push([v, w]);
g[v].push([u, w]);
}
let maxLen = 0, minNodes = n+1;
function dfs(u: number, p: number, st: Set<number>, len: number, nodes: number) {
if (len > maxLen || (len === maxLen && nodes < minNodes)) {
maxLen = len;
minNodes = nodes;
}
for (const [v, w] of g[u]) {
if (v === p || st.has(nums[v])) continue;
st.add(nums[v]);
dfs(v, u, st, len + w, nodes + 1);
st.delete(nums[v]);
}
}
for (let i = 0; i < n; ++i) {
dfs(i, -1, new Set([nums[i]]), 0, 1);
}
return [maxLen, minNodes];
}
}
Complexity
- ⏰ Time complexity:
O(n^2), as we start DFS from each node and visit each edge once per start node. - 🧺 Space complexity:
O(n), for the set used in each DFS call.