Longest Special Path II
Problem
You are given an undirected tree rooted at node 0, with n nodes numbered from 0 to n - 1. This is represented by a 2D array edges of length n -1, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui
and vi with length lengthi. You are also given an integer array nums, where nums[i] represents the value at node i.
A special path is defined as a downward path from an ancestor node to a descendant node in which all node values are distinct , except for at most one value that may appear twice.
Return an array result of size 2, where result[0] is the length of the
longest special path, and result[1] is the minimum number of nodes in all possible longest special paths.
Examples
Example 1
Input: edges =
[[0,1,1],[1,2,3],[1,3,1],[2,4,6],[4,7,2],[3,5,2],[3,6,5],[6,8,3]], nums =
[1,1,0,3,1,2,1,1,0]
Output: [9,3]
Explanation:
In the image below, nodes are colored by their corresponding values in `nums`.
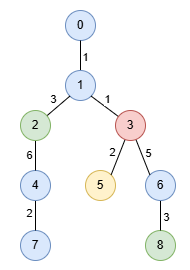
The longest special paths are `1 -> 2 -> 4` and `1 -> 3 -> 6 -> 8`, both
having a length of 9. The minimum number of nodes across all longest special
paths is 3.
Example 2
Input: edges = [[1,0,3],[0,2,4],[0,3,5]], nums = [1,1,0,2]
Output: [5,2]
Explanation:
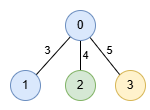
The longest path is `0 -> 3` consisting of 2 nodes with a length of 5.
Constraints
2 <= n <= 5 * 10^4edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= lengthi <= 10^3nums.length == n0 <= nums[i] <= 5 * 10^4- The input is generated such that
edgesrepresents a valid tree.
Solution
Method 1 – DFS with Value Count Tracking
Intuition
We need to find the longest downward path in a tree where all node values are distinct except for at most one value that may appear twice. We use DFS to explore all paths, tracking the count of each value in the current path. We allow at most one value to appear twice, and all others must be unique.
Approach
- Build the tree as an adjacency list from the edges.
- For each node, perform DFS:
- Track a counter (hash map or array) for the values in the current path.
- Track the number of values that appear twice.
- For each child, if adding its value does not make more than one value appear twice, continue DFS.
- Backtrack after visiting each child.
- For each node, start DFS and update the global answer if a longer or equally long path with fewer nodes is found.
- Return the maximum path length and minimum number of nodes for that length.
Code
C++
class Solution {
public:
vector<int> longestSpecialPath(vector<vector<int>>& edges, vector<int>& nums) {
int n = nums.size();
vector<vector<pair<int,int>>> g(n);
for (auto& e : edges) {
g[e[0]].push_back({e[1], e[2]});
g[e[1]].push_back({e[0], e[2]});
}
int maxLen = 0, minNodes = n+1;
function<void(int,int,unordered_map<int,int>&,int,int,int)> dfs = [&](int u, int p, unordered_map<int,int>& cnt, int twice, int len, int nodes) {
if (len > maxLen || (len == maxLen && nodes < minNodes)) {
maxLen = len;
minNodes = nodes;
}
for (auto& [v, w] : g[u]) {
if (v == p) continue;
cnt[nums[v]]++;
if (cnt[nums[v]] == 2) twice++;
if (cnt[nums[v]] <= 2 && twice <= 1) {
dfs(v, u, cnt, twice, len + w, nodes + 1);
}
if (cnt[nums[v]] == 2) twice--;
cnt[nums[v]]--;
}
};
for (int i = 0; i < n; ++i) {
unordered_map<int,int> cnt;
cnt[nums[i]] = 1;
dfs(i, -1, cnt, 0, 0, 1);
}
return {maxLen, minNodes};
}
};
Go
func longestSpecialPath(edges [][]int, nums []int) []int {
n := len(nums)
g := make([][][2]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
}
maxLen, minNodes := 0, n+1
var dfs func(u, p int, cnt map[int]int, twice, length, nodes int)
dfs = func(u, p int, cnt map[int]int, twice, length, nodes int) {
if length > maxLen || (length == maxLen && nodes < minNodes) {
maxLen = length
minNodes = nodes
}
for _, vw := range g[u] {
v, w := vw[0], vw[1]
if v == p {
continue
}
cnt[nums[v]]++
if cnt[nums[v]] == 2 {
twice++
}
if cnt[nums[v]] <= 2 && twice <= 1 {
dfs(v, u, cnt, twice, length+w, nodes+1)
}
if cnt[nums[v]] == 2 {
twice--
}
cnt[nums[v]]--
}
}
for i := 0; i < n; i++ {
cnt := map[int]int{nums[i]: 1}
dfs(i, -1, cnt, 0, 0, 1)
}
return []int{maxLen, minNodes}
}
Java
class Solution {
public int[] longestSpecialPath(int[][] edges, int[] nums) {
int n = nums.length;
List<int[]>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(new int[]{e[1], e[2]});
g[e[1]].add(new int[]{e[0], e[2]});
}
int[] ans = new int[]{0, n+1};
dfs(0, -1, new HashMap<>(), 0, 0, 1, g, nums, ans);
for (int i = 1; i < n; i++) {
dfs(i, -1, new HashMap<>(), 0, 0, 1, g, nums, ans);
}
return ans;
}
void dfs(int u, int p, Map<Integer,Integer> cnt, int twice, int len, int nodes, List<int[]>[] g, int[] nums, int[] ans) {
cnt.put(nums[u], cnt.getOrDefault(nums[u], 0) + 1);
if (len > ans[0] || (len == ans[0] && nodes < ans[1])) {
ans[0] = len;
ans[1] = nodes;
}
for (int[] vw : g[u]) {
int v = vw[0], w = vw[1];
if (v == p) continue;
cnt.put(nums[v], cnt.getOrDefault(nums[v], 0) + 1);
if (cnt.get(nums[v]) == 2) twice++;
if (cnt.get(nums[v]) <= 2 && twice <= 1) {
dfs(v, u, cnt, twice, len + w, nodes + 1, g, nums, ans);
}
if (cnt.get(nums[v]) == 2) twice--;
cnt.put(nums[v], cnt.get(nums[v]) - 1);
}
cnt.put(nums[u], cnt.get(nums[u]) - 1);
}
}
Kotlin
class Solution {
fun longestSpecialPath(edges: Array<IntArray>, nums: IntArray): IntArray {
val n = nums.size
val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (e in edges) {
g[e[0]].add(Pair(e[1], e[2]))
g[e[1]].add(Pair(e[0], e[2]))
}
var maxLen = 0
var minNodes = n+1
fun dfs(u: Int, p: Int, cnt: MutableMap<Int,Int>, twice: Int, len: Int, nodes: Int) {
if (len > maxLen || (len == maxLen && nodes < minNodes)) {
maxLen = len
minNodes = nodes
}
for ((v, w) in g[u]) {
if (v == p) continue
cnt[nums[v]] = cnt.getOrDefault(nums[v], 0) + 1
var t = twice
if (cnt[nums[v]] == 2) t++
if (cnt[nums[v]] <= 2 && t <= 1) {
dfs(v, u, cnt, t, len + w, nodes + 1)
}
if (cnt[nums[v]] == 2) t--
cnt[nums[v]] = cnt[nums[v]]!! - 1
}
}
for (i in 0 until n) {
val cnt = mutableMapOf(nums[i] to 1)
dfs(i, -1, cnt, 0, 0, 1)
}
return intArrayOf(maxLen, minNodes)
}
}
Python
class Solution:
def longestSpecialPath(self, edges: list[list[int]], nums: list[int]) -> list[int]:
from collections import defaultdict
n = len(nums)
g = defaultdict(list)
for u, v, w in edges:
g[u].append((v, w))
g[v].append((u, w))
max_len, min_nodes = 0, n+1
def dfs(u: int, p: int, cnt: dict[int,int], twice: int, length: int, nodes: int):
nonlocal max_len, min_nodes
if length > max_len or (length == max_len and nodes < min_nodes):
max_len = length
min_nodes = nodes
for v, w in g[u]:
if v == p:
continue
cnt[nums[v]] = cnt.get(nums[v], 0) + 1
t = twice
if cnt[nums[v]] == 2:
t += 1
if cnt[nums[v]] <= 2 and t <= 1:
dfs(v, u, cnt, t, length + w, nodes + 1)
if cnt[nums[v]] == 2:
t -= 1
cnt[nums[v]] -= 1
for i in range(n):
dfs(i, -1, {nums[i]: 1}, 0, 0, 1)
return [max_len, min_nodes]
Rust
impl Solution {
pub fn longest_special_path(edges: Vec<Vec<i32>>, nums: Vec<i32>) -> Vec<i32> {
use std::collections::{HashMap, HashSet};
let n = nums.len();
let mut g = vec![vec![]; n];
for e in edges.iter() {
g[e[0] as usize].push((e[1] as usize, e[2]));
g[e[1] as usize].push((e[0] as usize, e[2]));
}
let mut max_len = 0;
let mut min_nodes = n as i32 + 1;
fn dfs(u: usize, p: i32, cnt: &mut HashMap<i32,i32>, twice: i32, len: i32, nodes: i32, g: &Vec<Vec<(usize, i32)>>, nums: &Vec<i32>, max_len: &mut i32, min_nodes: &mut i32) {
if len > *max_len || (len == *max_len && nodes < *min_nodes) {
*max_len = len;
*min_nodes = nodes;
}
for &(v, w) in &g[u] {
if v as i32 == p { continue; }
*cnt.entry(nums[v]).or_insert(0) += 1;
let mut t = twice;
if cnt[&nums[v]] == 2 { t += 1; }
if cnt[&nums[v]] <= 2 && t <= 1 {
dfs(v, u as i32, cnt, t, len + w, nodes + 1, g, nums, max_len, min_nodes);
}
if cnt[&nums[v]] == 2 { t -= 1; }
*cnt.get_mut(&nums[v]).unwrap() -= 1;
}
}
for i in 0..n {
let mut cnt = HashMap::new();
cnt.insert(nums[i], 1);
dfs(i, -1, &mut cnt, 0, 0, 1, &g, &nums, &mut max_len, &mut min_nodes);
}
vec![max_len, min_nodes]
}
}
TypeScript
class Solution {
longestSpecialPath(edges: number[][], nums: number[]): number[] {
const n = nums.length;
const g: [number, number][][] = Array.from({length: n}, () => []);
for (const [u, v, w] of edges) {
g[u].push([v, w]);
g[v].push([u, w]);
}
let maxLen = 0, minNodes = n+1;
function dfs(u: number, p: number, cnt: Map<number, number>, twice: number, len: number, nodes: number) {
if (len > maxLen || (len === maxLen && nodes < minNodes)) {
maxLen = len;
minNodes = nodes;
}
for (const [v, w] of g[u]) {
if (v === p) continue;
cnt.set(nums[v], (cnt.get(nums[v]) ?? 0) + 1);
let t = twice;
if (cnt.get(nums[v]) === 2) t++;
if ((cnt.get(nums[v]) ?? 0) <= 2 && t <= 1) {
dfs(v, u, cnt, t, len + w, nodes + 1);
}
if (cnt.get(nums[v]) === 2) t--;
cnt.set(nums[v], (cnt.get(nums[v]) ?? 0) - 1);
}
}
for (let i = 0; i < n; ++i) {
dfs(i, -1, new Map([[nums[i], 1]]), 0, 0, 1);
}
return [maxLen, minNodes];
}
}
Complexity
- ⏰ Time complexity:
O(n^2), as we start DFS from each node and visit each edge once per start node. - 🧺 Space complexity:
O(n), for the value count map used in each DFS call.