problemmediumalgorithmsleetcode-1372leetcode 1372leetcode1372

Longest ZigZag Path in a Binary Tree

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

  • Choose any node in the binary tree and a direction (right or left).
  • If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
  • Change the direction from right to left or from left to right.
  • Repeat the second and third steps until you can't move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

Examples

Example 1:

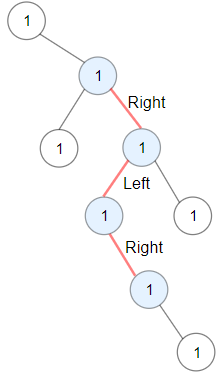
Input:
root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output:
 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

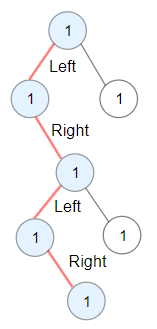
Input:
root = [1,1,1,null,1,null,null,1,1,null,1]
Output:
 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input:
root = [1]
Output:
 0

Solution

Method 1 - DFS with Recursion

Approach

We use depth-first search (DFS) to explore all possible ZigZag paths starting from every node. At each node, we recursively try both directions (left and right), switching direction at each step. We keep track of the current path length and update the global maximum whenever a longer ZigZag is found.

Recurrence Relation

Let dfs(node, direction, length) be the function that returns the longest ZigZag path starting from node, moving in direction (left or right), with current path length length.

  • If node is null, return.
  • If direction is left, next call is dfs(node.left, right, length + 1) and restart from node.right with length 1.
  • If direction is right, next call is dfs(node.right, left, length + 1) and restart from node.left with length 1.

Base Case

If the current node is null, the recursion stops.

Code

C++
class Solution {
public:
	int maxZigZag = 0;
	void dfs(TreeNode* node, bool left, int length) {
		if (!node) return;
		maxZigZag = std::max(maxZigZag, length);
		if (left) {
			dfs(node->left, false, length + 1);
			dfs(node->right, true, 1);
		} else {
			dfs(node->right, true, length + 1);
			dfs(node->left, false, 1);
		}
	}
	int longestZigZag(TreeNode* root) {
		dfs(root, true, 0);
		dfs(root, false, 0);
		return maxZigZag;
	}
};
Go
func longestZigZag(root *TreeNode) int {
	var maxZigZag int
	var dfs func(node *TreeNode, left bool, length int)
	dfs = func(node *TreeNode, left bool, length int) {
		if node == nil {
			return
		}
		if length > maxZigZag {
			maxZigZag = length
		}
		if left {
			dfs(node.Left, false, length+1)
			dfs(node.Right, true, 1)
		} else {
			dfs(node.Right, true, length+1)
			dfs(node.Left, false, 1)
		}
	}
	dfs(root, true, 0)
	dfs(root, false, 0)
	return maxZigZag
}
Java
class Solution {
	int maxZigZag = 0;
	public int longestZigZag(TreeNode root) {
		dfs(root, true, 0);
		dfs(root, false, 0);
		return maxZigZag;
	}
	private void dfs(TreeNode node, boolean left, int length) {
		if (node == null) return;
		maxZigZag = Math.max(maxZigZag, length);
		if (left) {
			dfs(node.left, false, length + 1);
			dfs(node.right, true, 1);
		} else {
			dfs(node.right, true, length + 1);
			dfs(node.left, false, 1);
		}
	}
}
Kotlin
class Solution {
	var maxZigZag = 0
	fun longestZigZag(root: TreeNode?): Int {
		dfs(root, true, 0)
		dfs(root, false, 0)
		return maxZigZag
	}
	private fun dfs(node: TreeNode?, left: Boolean, length: Int) {
		if (node == null) return
		maxZigZag = maxOf(maxZigZag, length)
		if (left) {
			dfs(node.left, false, length + 1)
			dfs(node.right, true, 1)
		} else {
			dfs(node.right, true, length + 1)
			dfs(node.left, false, 1)
		}
	}
}
Python
class Solution:
	def longestZigZag(self, root: Optional[TreeNode]) -> int:
		self.maxZigZag = 0
		def dfs(node, left, length):
			if not node:
				return
			self.maxZigZag = max(self.maxZigZag, length)
			if left:
				dfs(node.left, False, length + 1)
				dfs(node.right, True, 1)
			else:
				dfs(node.right, True, length + 1)
				dfs(node.left, False, 1)
		dfs(root, True, 0)
		dfs(root, False, 0)
		return self.maxZigZag
Rust
impl Solution {
	pub fn longest_zig_zag(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
		fn dfs(node: Option<Rc<RefCell<TreeNode>>>, left: bool, length: i32, max_zigzag: &mut i32) {
			if let Some(n) = node {
				*max_zigzag = (*max_zigzag).max(length);
				let n = n.borrow();
				if left {
					dfs(n.left.clone(), false, length + 1, max_zigzag);
					dfs(n.right.clone(), true, 1, max_zigzag);
				} else {
					dfs(n.right.clone(), true, length + 1, max_zigzag);
					dfs(n.left.clone(), false, 1, max_zigzag);
				}
			}
		}
		let mut max_zigzag = 0;
		dfs(root.clone(), true, 0, &mut max_zigzag);
		dfs(root, false, 0, &mut max_zigzag);
		max_zigzag
	}
}
TypeScript
class Solution {
	maxZigZag = 0;
	longestZigZag(root: TreeNode | null): number {
		this.dfs(root, true, 0);
		this.dfs(root, false, 0);
		return this.maxZigZag;
	}
	private dfs(node: TreeNode | null, left: boolean, length: number): void {
		if (!node) return;
		this.maxZigZag = Math.max(this.maxZigZag, length);
		if (left) {
			this.dfs(node.left, false, length + 1);
			this.dfs(node.right, true, 1);
		} else {
			this.dfs(node.right, true, length + 1);
			this.dfs(node.left, false, 1);
		}
	}
}

Complexity

  • ⏰ Time complexity: O(N), because each node in the tree is visited a constant number of times by the DFS traversal.
  • 🧺 Space complexity: O(H), where H is the height of the tree, due to the recursion stack. In the worst case (a skewed tree), H = N.

Comments