Make Costs of Paths Equal in a Binary Tree

Problem

You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.

Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.

Return theminimum number of increments you need to make the cost of paths from the root to each leaf node equal.

Note :

A perfect binary tree is a tree where each node, except the leaf nodes, has exactly 2 children.
The cost of a path is the sum of costs of nodes in the path.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12



![](https://assets.leetcode.com/uploads/2023/04/04/binaryytreeedrawio-4.png)

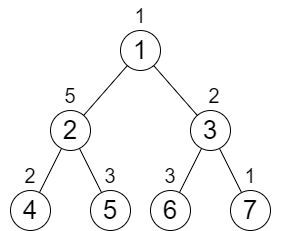
Input: n = 7, cost = [1,5,2,2,3,3,1]
Output: 6
Explanation: We can do the following increments:
- Increase the cost of node 4 one time.
- Increase the cost of node 3 three times.
- Increase the cost of node 7 two times.
Each path from the root to a leaf will have a total cost of 9.
The total increments we did is 1 + 3 + 2 = 6.
It can be shown that this is the minimum answer we can achieve.

Example 2

1
2
3
4
5
6



![](https://assets.leetcode.com/uploads/2023/04/04/binaryytreee2drawio.png)

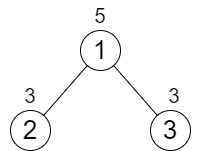
Input: n = 3, cost = [5,3,3]
Output: 0
Explanation: The two paths already have equal total costs, so no increments are needed.

Constraints

3 <= n <= 10^5
n + 1 is a power of 2
cost.length == n
1 <= cost[i] <= 10^4

Solution

Method 1 – DFS with Postorder Traversal

Intuition

To make all root-to-leaf path costs equal in a perfect binary tree, we need to increment node costs so that all paths sum to the same value. We can use postorder DFS to compute the maximum path sum for each subtree and count the increments needed to balance the left and right subtrees at each node.

Approach

Define a recursive DFS function that returns the maximum path sum from the current node to any leaf and accumulates the total increments needed.
For each node, recursively compute the left and right subtree path sums.
The number of increments needed at this node is the absolute difference between left and right subtree path sums.
Add the node’s cost to the maximum of the left and right subtree sums and return it up the recursion.
The total increments is the sum of all increments at each node.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
public:
    int minIncrements(int n, vector<int>& cost) {
        int ans = 0;
        function<int(int)> dfs = [&](int i) -> int {
            if (2*i+1 >= n) return cost[i];
            int l = dfs(2*i+1), r = dfs(2*i+2);
            ans += abs(l - r);
            return cost[i] + max(l, r);
        };
        dfs(0);
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


func minIncrements(n int, cost []int) int {
    ans := 0
    var dfs func(i int) int
    dfs = func(i int) int {
        if 2*i+1 >= n {
            return cost[i]
        }
        l := dfs(2*i+1)
        r := dfs(2*i+2)
        if l > r {
            ans += l - r
        } else {
            ans += r - l
        }
        if l > r {
            return cost[i] + l
        }
        return cost[i] + r
    }
    dfs(0)
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    int ans = 0;
    public int minIncrements(int n, int[] cost) {
        dfs(0, n, cost);
        return ans;
    }
    int dfs(int i, int n, int[] cost) {
        if (2*i+1 >= n) return cost[i];
        int l = dfs(2*i+1, n, cost), r = dfs(2*i+2, n, cost);
        ans += Math.abs(l - r);
        return cost[i] + Math.max(l, r);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
    var ans = 0
    fun minIncrements(n: Int, cost: IntArray): Int {
        fun dfs(i: Int): Int {
            if (2*i+1 >= n) return cost[i]
            val l = dfs(2*i+1)
            val r = dfs(2*i+2)
            ans += kotlin.math.abs(l - r)
            return cost[i] + maxOf(l, r)
        }
        dfs(0)
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution:
    def minIncrements(self, n: int, cost: list[int]) -> int:
        ans = 0
        def dfs(i: int) -> int:
            nonlocal ans
            if 2*i+1 >= n:
                return cost[i]
            l = dfs(2*i+1)
            r = dfs(2*i+2)
            ans += abs(l - r)
            return cost[i] + max(l, r)
        dfs(0)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


impl Solution {
    pub fn min_increments(n: i32, cost: Vec<i32>) -> i32 {
        fn dfs(i: usize, n: usize, cost: &Vec<i32>, ans: &mut i32) -> i32 {
            if 2*i+1 >= n {
                return cost[i];
            }
            let l = dfs(2*i+1, n, cost, ans);
            let r = dfs(2*i+2, n, cost, ans);
            *ans += (l - r).abs();
            cost[i] + l.max(r)
        }
        let mut ans = 0;
        dfs(0, n as usize, &cost, &mut ans);
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    minIncrements(n: number, cost: number[]): number {
        let ans = 0;
        function dfs(i: number): number {
            if (2*i+1 >= n) return cost[i];
            const l = dfs(2*i+1), r = dfs(2*i+2);
            ans += Math.abs(l - r);
            return cost[i] + Math.max(l, r);
        }
        dfs(0);
        return ans;
    }
}

Complexity

⏰ Time complexity: O(n), as each node is visited once.
🧺 Space complexity: O(h), where h is the height of the tree (recursive stack).

Problem#

Examples#

Example 1#

Example 2#

Constraints#

Solution#

Method 1 – DFS with Postorder Traversal#

Intuition#

Approach#

Code#

Complexity#