Manhattan Distances of All Arrangements of Pieces
Problem
You are given three integers m, n, and k.
There is a rectangular grid of size m × n containing k identical pieces.
Return the sum of Manhattan distances between every pair of pieces over all
valid arrangements of pieces.
A valid arrangement is a placement of all k pieces on the grid with at most one piece per cell.
Since the answer may be very large, return it modulo 10^9 + 7.
The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi -xj| + |yi - yj|.
Examples
Example 1
Input: m = 2, n = 2, k = 2
Output: 8
Explanation:
The valid arrangements of pieces on the board are:
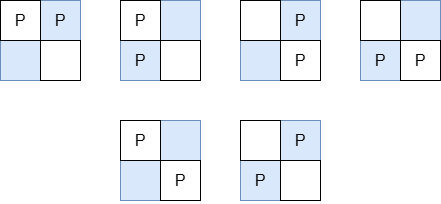
* In the first 4 arrangements, the Manhattan distance between the two pieces is 1.
* In the last 2 arrangements, the Manhattan distance between the two pieces is 2.
Thus, the total Manhattan distance across all valid arrangements is `1 + 1 + 1
+ 1 + 2 + 2 = 8`.
Example 2
Input: m = 1, n = 4, k = 3
Output: 20
Explanation:
The valid arrangements of pieces on the board are:

* The first and last arrangements have a total Manhattan distance of `1 + 1 + 2 = 4`.
* The middle two arrangements have a total Manhattan distance of `1 + 2 + 3 = 6`.
The total Manhattan distance between all pairs of pieces across all
arrangements is `4 + 6 + 6 + 4 = 20`.
Constraints
1 <= m, n <= 10^52 <= m * n <= 10^52 <= k <= m * n
Solution
Method 1 – Combinatorial Counting with Precomputed Sums
Intuition
The sum of Manhattan distances over all valid arrangements can be computed by considering all pairs of cells and counting how many arrangements place two pieces at those cells and the rest elsewhere. The number of such arrangements is C(m*n-2, k-2). We sum the Manhattan distance for each pair, multiplied by the number of ways to choose the remaining pieces.
Approach
- Precompute factorials and inverse factorials up to m*n for fast binomial coefficients modulo 1e9+7.
- For each pair of cells (i1, j1) and (i2, j2), compute their Manhattan distance and count the number of arrangements: C(m*n-2, k-2).
- For efficiency, sum the contributions for all pairs by row and by column separately, using the formula for sum of absolute differences.
- Multiply the total sum by C(m*n-2, k-2) and take modulo 1e9+7.
Code
C++
const int MOD = 1e9+7;
long long modpow(long long a, long long b, long long mod) {
long long res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
vector<long long> fact, invfact;
void init(int n) {
fact.resize(n+1, 1);
invfact.resize(n+1, 1);
for (int i = 1; i <= n; ++i) fact[i] = fact[i-1] * i % MOD;
invfact[n] = modpow(fact[n], MOD-2, MOD);
for (int i = n-1; i >= 0; --i) invfact[i] = invfact[i+1] * (i+1) % MOD;
}
long long C(int n, int k) {
if (k < 0 || k > n) return 0;
return fact[n] * invfact[k] % MOD * invfact[n-k] % MOD;
}
class Solution {
public:
int sumDistance(int m, int n, int k) {
int N = m * n;
init(N);
long long ans = 0;
// Row contribution
for (int i = 0; i < m; ++i) {
for (int j = i+1; j < m; ++j) {
long long cnt = n * n * (j - i);
ans = (ans + cnt * C(N-2, k-2)) % MOD;
}
}
// Col contribution
for (int i = 0; i < n; ++i) {
for (int j = i+1; j < n; ++j) {
long long cnt = m * m * (j - i);
ans = (ans + cnt * C(N-2, k-2)) % MOD;
}
}
return ans;
}
};
Go
const MOD = 1e9 + 7
func modpow(a, b, mod int) int {
res := 1
for b > 0 {
if b&1 == 1 {
res = res * a % mod
}
a = a * a % mod
b >>= 1
}
return res
}
func sumDistance(m, n, k int) int {
N := m * n
fact := make([]int, N+1)
invfact := make([]int, N+1)
fact[0] = 1
for i := 1; i <= N; i++ {
fact[i] = fact[i-1] * i % MOD
}
invfact[N] = modpow(fact[N], MOD-2, MOD)
for i := N - 1; i >= 0; i-- {
invfact[i] = invfact[i+1] * (i+1) % MOD
}
C := func(n, k int) int {
if k < 0 || k > n {
return 0
}
return fact[n] * invfact[k] % MOD * invfact[n-k] % MOD
}
ans := 0
for i := 0; i < m; i++ {
for j := i+1; j < m; j++ {
cnt := n * n * (j - i) % MOD
ans = (ans + cnt * C(N-2, k-2) % MOD) % MOD
}
}
for i := 0; i < n; i++ {
for j := i+1; j < n; j++ {
cnt := m * m * (j - i) % MOD
ans = (ans + cnt * C(N-2, k-2) % MOD) % MOD
}
}
return ans
}
Java
class Solution {
static final int MOD = 1_000_000_007;
long[] fact, invfact;
void init(int n) {
fact = new long[n+1];
invfact = new long[n+1];
fact[0] = 1;
for (int i = 1; i <= n; i++) fact[i] = fact[i-1] * i % MOD;
invfact[n] = pow(fact[n], MOD-2);
for (int i = n-1; i >= 0; i--) invfact[i] = invfact[i+1] * (i+1) % MOD;
}
long pow(long a, long b) {
long res = 1;
while (b > 0) {
if ((b & 1) == 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
long C(int n, int k) {
if (k < 0 || k > n) return 0;
return fact[n] * invfact[k] % MOD * invfact[n-k] % MOD;
}
public int sumDistance(int m, int n, int k) {
int N = m * n;
init(N);
long ans = 0;
for (int i = 0; i < m; i++) {
for (int j = i+1; j < m; j++) {
long cnt = 1L * n * n * (j - i);
ans = (ans + cnt * C(N-2, k-2)) % MOD;
}
}
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
long cnt = 1L * m * m * (j - i);
ans = (ans + cnt * C(N-2, k-2)) % MOD;
}
}
return (int)ans;
}
}
Kotlin
class Solution {
private val MOD = 1_000_000_007L
private lateinit var fact: LongArray
private lateinit var invfact: LongArray
private fun pow(a: Long, b: Long): Long {
var res = 1L
var aa = a
var bb = b
while (bb > 0) {
if (bb and 1L == 1L) res = res * aa % MOD
aa = aa * aa % MOD
bb = bb shr 1
}
return res
}
private fun init(n: Int) {
fact = LongArray(n+1) { 1L }
invfact = LongArray(n+1) { 1L }
for (i in 1..n) fact[i] = fact[i-1] * i % MOD
invfact[n] = pow(fact[n], MOD-2)
for (i in n-1 downTo 0) invfact[i] = invfact[i+1] * (i+1) % MOD
}
private fun C(n: Int, k: Int): Long {
if (k < 0 || k > n) return 0L
return fact[n] * invfact[k] % MOD * invfact[n-k] % MOD
}
fun sumDistance(m: Int, n: Int, k: Int): Int {
val N = m * n
init(N)
var ans = 0L
for (i in 0 until m) {
for (j in i+1 until m) {
val cnt = n.toLong() * n * (j - i)
ans = (ans + cnt % MOD * C(N-2, k-2) % MOD) % MOD
}
}
for (i in 0 until n) {
for (j in i+1 until n) {
val cnt = m.toLong() * m * (j - i)
ans = (ans + cnt % MOD * C(N-2, k-2) % MOD) % MOD
}
}
return ans.toInt()
}
}
Python
class Solution:
def sumDistance(self, m: int, n: int, k: int) -> int:
MOD = 10**9 + 7
from math import comb
N = m * n
if k < 2:
return 0
c = comb(N-2, k-2)
ans = 0
for i in range(m):
for j in range(i+1, m):
cnt = n * n * (j - i)
ans = (ans + cnt * c) % MOD
for i in range(n):
for j in range(i+1, n):
cnt = m * m * (j - i)
ans = (ans + cnt * c) % MOD
return ans
Rust
const MOD: i64 = 1_000_000_007;
fn modpow(mut a: i64, mut b: i64, m: i64) -> i64 {
let mut res = 1;
while b > 0 {
if b & 1 == 1 {
res = res * a % m;
}
a = a * a % m;
b >>= 1;
}
res
}
fn comb(n: i64, k: i64, fact: &Vec<i64>, invfact: &Vec<i64>) -> i64 {
if k < 0 || k > n { return 0; }
fact[n as usize] * invfact[k as usize] % MOD * invfact[(n-k) as usize] % MOD
}
impl Solution {
pub fn sum_distance(m: i32, n: i32, k: i32) -> i32 {
let N = (m * n) as i64;
let mut fact = vec![1; (N+1) as usize];
let mut invfact = vec![1; (N+1) as usize];
for i in 1..=N as usize {
fact[i] = fact[i-1] * i as i64 % MOD;
}
invfact[N as usize] = modpow(fact[N as usize], MOD-2, MOD);
for i in (0..N as usize).rev() {
invfact[i] = invfact[i+1] * (i as i64 + 1) % MOD;
}
let c = comb(N-2, k as i64-2, &fact, &invfact);
let mut ans = 0i64;
for i in 0..m {
for j in i+1..m {
let cnt = n as i64 * n as i64 * (j-i) as i64;
ans = (ans + cnt * c % MOD) % MOD;
}
}
for i in 0..n {
for j in i+1..n {
let cnt = m as i64 * m as i64 * (j-i) as i64;
ans = (ans + cnt * c % MOD) % MOD;
}
}
ans as i32
}
}
TypeScript
class Solution {
private MOD = 1_000_000_007;
private fact: number[] = [];
private invfact: number[] = [];
private pow(a: number, b: number): number {
let res = 1;
while (b > 0) {
if (b & 1) res = res * a % this.MOD;
a = a * a % this.MOD;
b >>= 1;
}
return res;
}
private init(n: number) {
this.fact = Array(n+1).fill(1);
this.invfact = Array(n+1).fill(1);
for (let i = 1; i <= n; i++) this.fact[i] = this.fact[i-1] * i % this.MOD;
this.invfact[n] = this.pow(this.fact[n], this.MOD-2);
for (let i = n-1; i >= 0; i--) this.invfact[i] = this.invfact[i+1] * (i+1) % this.MOD;
}
private C(n: number, k: number): number {
if (k < 0 || k > n) return 0;
return this.fact[n] * this.invfact[k] % this.MOD * this.invfact[n-k] % this.MOD;
}
sumDistance(m: number, n: number, k: number): number {
const N = m * n;
this.init(N);
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = i+1; j < m; j++) {
const cnt = n * n * (j - i);
ans = (ans + cnt * this.C(N-2, k-2)) % this.MOD;
}
}
for (let i = 0; i < n; i++) {
for (let j = i+1; j < n; j++) {
const cnt = m * m * (j - i);
ans = (ans + cnt * this.C(N-2, k-2)) % this.MOD;
}
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O((m+n)^2 + m*n), for precomputing factorials and iterating over all pairs of rows and columns. - 🧺 Space complexity:
O(m*n), for storing factorials and inverse factorials.