Matrix Similarity After Cyclic Shifts

Problem

You are given an m x n integer matrix mat and an integer k. The matrix rows are 0-indexed.

The following proccess happens k times:

• Even-indexed rows (0, 2, 4, ...) are cyclically shifted to the left.

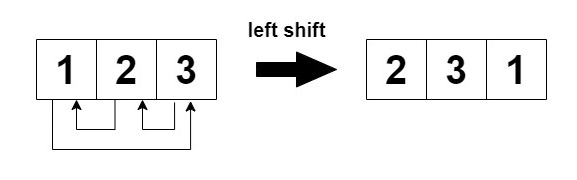
• Odd-indexed rows (1, 3, 5, ...) are cyclically shifted to the right.

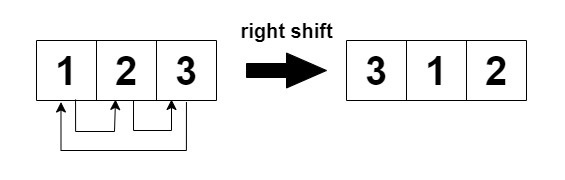
Return true if the final modified matrix after k steps is identical to the original matrix, and false otherwise.

Examples

Example 1

Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 4

Output: false

Explanation:

In each step left shift is applied to rows 0 and 2 (even indices), and right
shift to row 1 (odd index).

![](https://assets.leetcode.com/uploads/2024/05/19/t1-2.jpg)

Example 2

Input: mat = [[1,2,1,2],[5,5,5,5],[6,3,6,3]], k = 2

Output: true

Explanation:

![](https://assets.leetcode.com/uploads/2024/05/19/t1-3.jpg)

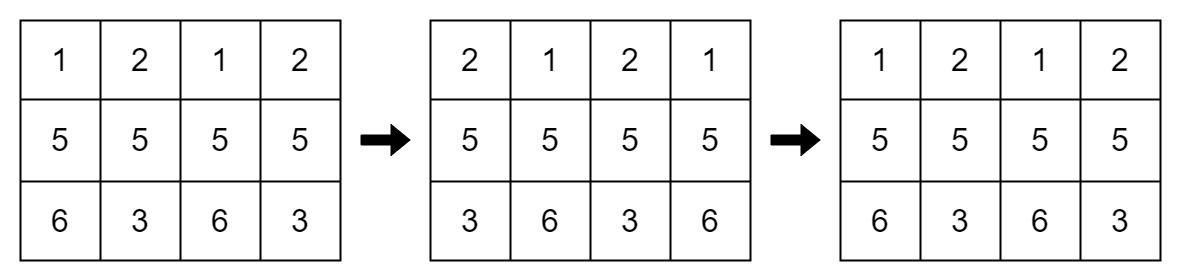
Example 3

Input: mat = [[2,2],[2,2]], k = 3

Output: true

Explanation:

As all the values are equal in the matrix, even after performing cyclic shifts
the matrix will remain the same.

Constraints

• 1 <= mat.length <= 25
• 1 <= mat[i].length <= 25
• 1 <= mat[i][j] <= 25
• 1 <= k <= 50

Solution

Method 1 – Simulation with Modulo Shifts

Intuition

Each row is shifted left or right cyclically, depending on its index parity, for k times. After all shifts, we compare the resulting matrix to the original. Since shifting by the row length is a full cycle, we use modulo to optimize the number of shifts.

Approach

1. For each row in the matrix:
   • If the row index is even, shift left by k % n positions.
   • If the row index is odd, shift right by k % n positions.
2. After all shifts, compare the resulting matrix to the original.
3. Return true if they are identical, else false.

Code

C++

class Solution {
public:
    bool areSimilar(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        for (int i = 0; i < m; ++i) {
            vector<int> row(n);
            for (int j = 0; j < n; ++j) {
                int idx = (i % 2 == 0) ? (j + k) % n : (j - k + n) % n;
                row[j] = mat[i][idx];
            }
            if (row != mat[i]) return false;
        }
        return true;
    }
};

Go

func areSimilar(mat [][]int, k int) bool {
    m, n := len(mat), len(mat[0])
    for i := 0; i < m; i++ {
        row := make([]int, n)
        for j := 0; j < n; j++ {
            var idx int
            if i%2 == 0 {
                idx = (j + k) % n
            } else {
                idx = (j - k + n) % n
            }
            row[j] = mat[i][idx]
        }
        for j := 0; j < n; j++ {
            if row[j] != mat[i][j] {
                return false
            }
        }
    }
    return true
}

Java

class Solution {
    public boolean areSimilar(int[][] mat, int k) {
        int m = mat.length, n = mat[0].length;
        for (int i = 0; i < m; i++) {
            int[] row = new int[n];
            for (int j = 0; j < n; j++) {
                int idx = (i % 2 == 0) ? (j + k) % n : (j - k + n) % n;
                row[j] = mat[i][idx];
            }
            for (int j = 0; j < n; j++) {
                if (row[j] != mat[i][j]) return false;
            }
        }
        return true;
    }
}

Kotlin

class Solution {
    fun areSimilar(mat: Array<IntArray>, k: Int): Boolean {
        val m = mat.size
        val n = mat[0].size
        for (i in 0 until m) {
            val row = IntArray(n)
            for (j in 0 until n) {
                val idx = if (i % 2 == 0) (j + k) % n else (j - k + n) % n
                row[j] = mat[i][idx]
            }
            if (!row.contentEquals(mat[i])) return false
        }
        return true
    }
}

Python

class Solution:
    def areSimilar(self, mat: list[list[int]], k: int) -> bool:
        m, n = len(mat), len(mat[0])
        for i in range(m):
            row = [(mat[i][(j + k) % n] if i % 2 == 0 else mat[i][(j - k) % n]) for j in range(n)]
            if row != mat[i]:
                return False
        return True

Rust

impl Solution {
    pub fn are_similar(mat: Vec<Vec<i32>>, k: i32) -> bool {
        let m = mat.len();
        let n = mat[0].len();
        for i in 0..m {
            let mut row = vec![0; n];
            for j in 0..n {
                let idx = if i % 2 == 0 {
                    (j + k as usize) % n
                } else {
                    (j + n - (k as usize % n)) % n
                };
                row[j] = mat[i][idx];
            }
            if row != mat[i] {
                return false;
            }
        }
        true
    }
}

TypeScript

class Solution {
    areSimilar(mat: number[][], k: number): boolean {
        const m = mat.length, n = mat[0].length;
        for (let i = 0; i < m; i++) {
            const row = new Array(n);
            for (let j = 0; j < n; j++) {
                const idx = i % 2 === 0 ? (j + k) % n : (j - k + n) % n;
                row[j] = mat[i][idx];
            }
            for (let j = 0; j < n; j++) {
                if (row[j] !== mat[i][j]) return false;
            }
        }
        return true;
    }
}

Complexity

• ⏰ Time complexity: O(mn), where m and n are the matrix dimensions, as we process each cell once.
• 🧺 Space complexity: O(n), for the temporary row array.