Problem

There is a city composed of n x n blocks, where each block contains a single building shaped like a vertical square prism. You are given a 0-indexed n x n integer matrix grid where grid[r][c] represents the height of the building located in the block at row r and column c.

A city’s skyline is the outer contour formed by all the building when viewing the side of the city from a distance. The skyline from each cardinal direction north, east, south, and west may be different.

We are allowed to increase the height of any number of buildings by any amount (the amount can be different per building). The height of a 0-height building can also be increased. However, increasing the height of a building should not affect the city’s skyline from any cardinal direction.

Return themaximum total sum that the height of the buildings can be increased by without changing the city’s skyline from any cardinal direction.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


![](https://assets.leetcode.com/uploads/2021/06/21/807-ex1.png)

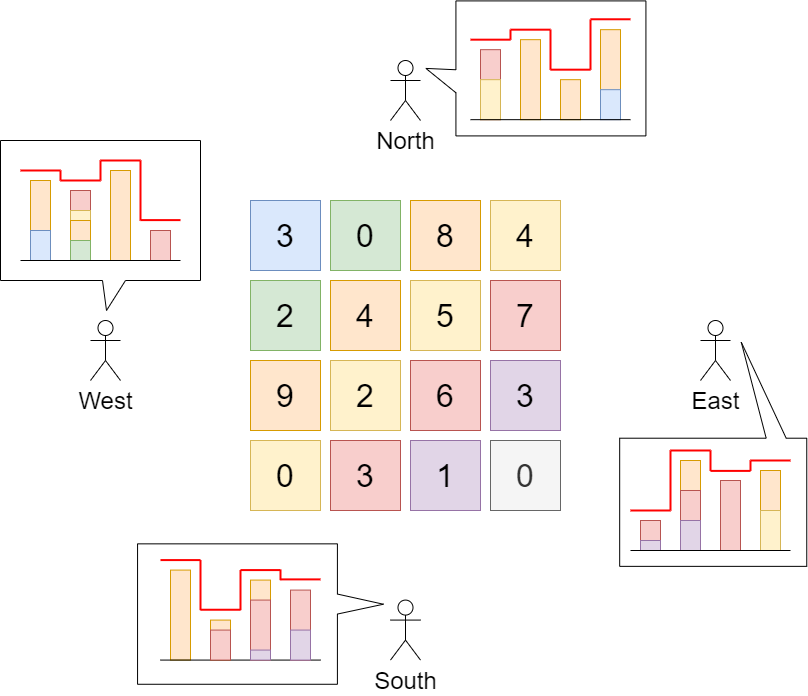
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
            [7, 4, 7, 7],
            [9, 4, 8, 7],
            [3, 3, 3, 3] ]

Example 2

1
2
3

Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: Increasing the height of any building will result in the skyline changing.

Constraints

  • n == grid.length
  • n == grid[r].length
  • 2 <= n <= 50
  • 0 <= grid[r][c] <= 100

Solution

Method 1 – Greedy by Row and Column Maximums

Intuition

To keep the skyline unchanged, the height of each building can be increased up to the minimum of the maximum height in its row and column. This ensures the skyline from all four directions remains the same.

Approach

  1. For each row, compute the maximum height (row max).
  2. For each column, compute the maximum height (column max).
  3. For each cell (i, j), the new height can be at most min(row_max[i], col_max[j]).
  4. The increase for each cell is min(row_max[i], col_max[j]) - grid[i][j].
  5. Sum all increases and return the total.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int maxIncreaseKeepingSkyline(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<int> row_max(n, 0), col_max(n, 0);
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j) {
                row_max[i] = max(row_max[i], grid[i][j]);
                col_max[j] = max(col_max[j], grid[i][j]);
            }
        int ans = 0;
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                ans += min(row_max[i], col_max[j]) - grid[i][j];
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

func maxIncreaseKeepingSkyline(grid [][]int) int {
    n := len(grid)
    rowMax := make([]int, n)
    colMax := make([]int, n)
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] > rowMax[i] {
                rowMax[i] = grid[i][j]
            }
            if grid[i][j] > colMax[j] {
                colMax[j] = grid[i][j]
            }
        }
    }
    ans := 0
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            if rowMax[i] < colMax[j] {
                ans += rowMax[i] - grid[i][j]
            } else {
                ans += colMax[j] - grid[i][j]
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int maxIncreaseKeepingSkyline(int[][] grid) {
        int n = grid.length;
        int[] rowMax = new int[n], colMax = new int[n];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++) {
                rowMax[i] = Math.max(rowMax[i], grid[i][j]);
                colMax[j] = Math.max(colMax[j], grid[i][j]);
            }
        int ans = 0;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                ans += Math.min(rowMax[i], colMax[j]) - grid[i][j];
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    fun maxIncreaseKeepingSkyline(grid: Array<IntArray>): Int {
        val n = grid.size
        val rowMax = IntArray(n)
        val colMax = IntArray(n)
        for (i in 0 until n)
            for (j in 0 until n) {
                rowMax[i] = maxOf(rowMax[i], grid[i][j])
                colMax[j] = maxOf(colMax[j], grid[i][j])
            }
        var ans = 0
        for (i in 0 until n)
            for (j in 0 until n)
                ans += minOf(rowMax[i], colMax[j]) - grid[i][j]
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def maxIncreaseKeepingSkyline(self, grid: list[list[int]]) -> int:
        n = len(grid)
        row_max = [max(row) for row in grid]
        col_max = [max(grid[i][j] for i in range(n)) for j in range(n)]
        ans = 0
        for i in range(n):
            for j in range(n):
                ans += min(row_max[i], col_max[j]) - grid[i][j]
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

impl Solution {
    pub fn max_increase_keeping_skyline(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut row_max = vec![0; n];
        let mut col_max = vec![0; n];
        for i in 0..n {
            for j in 0..n {
                row_max[i] = row_max[i].max(grid[i][j]);
                col_max[j] = col_max[j].max(grid[i][j]);
            }
        }
        let mut ans = 0;
        for i in 0..n {
            for j in 0..n {
                ans += row_max[i].min(col_max[j]) - grid[i][j];
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    maxIncreaseKeepingSkyline(grid: number[][]): number {
        const n = grid.length;
        const rowMax = Array(n).fill(0);
        const colMax = Array(n).fill(0);
        for (let i = 0; i < n; i++)
            for (let j = 0; j < n; j++) {
                rowMax[i] = Math.max(rowMax[i], grid[i][j]);
                colMax[j] = Math.max(colMax[j], grid[i][j]);
            }
        let ans = 0;
        for (let i = 0; i < n; i++)
            for (let j = 0; j < n; j++)
                ans += Math.min(rowMax[i], colMax[j]) - grid[i][j];
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), where n is the grid size, as we scan all cells multiple times.
  • 🧺 Space complexity: O(n), for storing row and column maximums.