Problem
Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1‘s and return its area.
Examples
Example 1:
Input: matrix = [
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
Output: 4
$$ \begin{array}{|c|c|c|c|c|} \hline 1 & 0 & 1 & 0 & 0 \\ \hline 1 & 0 & \colorbox{orange} 1 & \colorbox{orange} 1 & 1 \\ \hline 1 & 1 & \colorbox{orange} 1 & \colorbox{orange} 1 & 1 \\ \hline 1 & 0 & 0 & 1 & 0 \\ \hline \end{array} \text{ OR } \begin{array}{|c|c|c|c|c|} \hline 1 & 0 & 1 & 0 & 0 \\ \hline 1 & 0 & 1 & \colorbox{orange} 1 & \colorbox{orange} 1 \\ \hline 1 & 1 & 1 & \colorbox{orange} 1 & \colorbox{orange} 1 \\ \hline 1 & 0 & 0 & 1 & 0 \\ \hline \end{array} $$
Solution
Method 1 - Bottom up DP 🏆
To solve this problem, we can use dynamic programming.
Intuition
Now, if we have a cell with 1 , is a square of size 1x1.
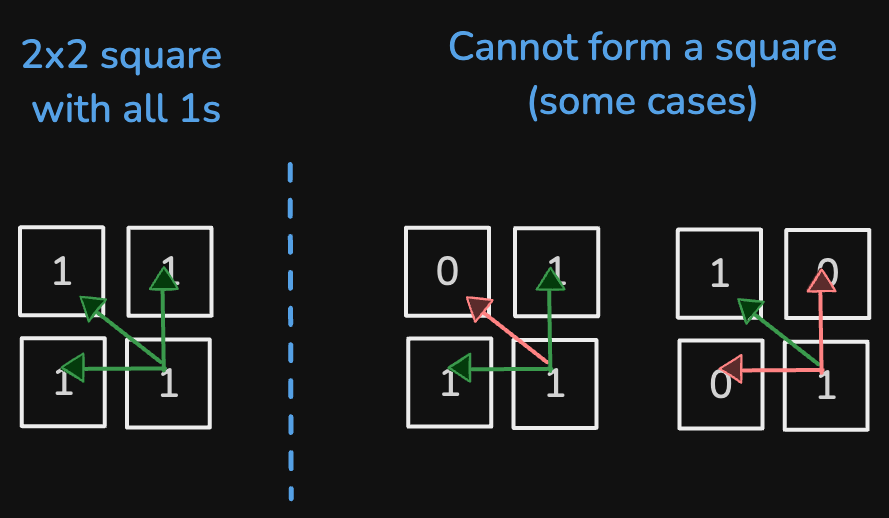
$$ \begin{array}{|c|} \hline 1 \\ \hline \end{array} $$ Similarly, a 2x2 square will have all 1s: $$ \begin{array}{|c|c|} \hline 1 & 1 \\ \hline 1 & 1 \\ \hline \end{array} $$
But if we find a 0 in that square, that will disrupt creation of square. These are all invalid squares:
$$
\begin{array}{|c|c|}
\hline
\colorbox{red} 0 & 1 \\
\hline
1 & 1 \\
\hline
\end{array}
\text{ }
\begin{array}{|c|c|}
\hline
1 & \colorbox{red} 0 \\
\hline
\colorbox{red} 0 & 1 \\
\hline
\end{array}
\text{ and so on..}
$$
But how can we use it to build the solution. So, when we iterate the matrix row-wise and column-wise, when the element is 1, it can be part of the square we have seen so far, provided it is surrounding elements are all 1s as well. Surrounding elements are - top, left, top-left.
Building the DP Grid
First we create a dp grid of size m * n, with all values initially set to 0.
Now, we will use dynamic programming to find this squares. As we iterate through the matrix from the top-left to the bottom-right, for each cell (i, j), when the value is 1, we consider the surrounding elements:
dp[i][j] = 1 + dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
Initial 1 as this 1 implies we already have 1x1 square. But if it has surrounding elements as all 1s, we can grow the square.
Approach
The idea is to use a 2D array dp where dp[i][j] represents the side length of the largest square whose bottom-right corner is the cell (i, j) in the given matrix.
- If
matrix[i][j]is ‘0’, thendp[i][j]will be 0 because no square can end at a cell that contains ‘0’. - If
matrix[i][j]is ‘1’, thendp[i][j]depends on the minimum of the three surrounding adjacent squares (left, top, and top-left) plus one. Specifically:dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1.
The result will be the maximum value found in the dp array, which represents the side length of the largest square. The area can be found by squaring this value. But if any of the value is not 1, that we cannot form the square, resulting in breaking of square.
Dry Run
Lets take input:
matrix = [
["1","0","1","0","0"],
["0","1","1","1","0"],
["0","1","1","1","0"],
["1","1","1","1","1"]
]
m = 4, n = 5
Code
Java
class Solution {
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
int m = matrix.length, n = matrix[0].length;
int[][] dp = new int[m][n];
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
ans = Math.max(ans, dp[i][j]);
}
}
}
return ans * ans;
}
}
Python
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix or not matrix[0]:
return 0
m, n = len(matrix), len(matrix[0])
dp: List[List[int]] = [[0] * n for _ in range(m)]
ans: int = 0
for i in range(m):
for j in range(n):
if matrix[i][j] == '1':
if i == 0 or j == 0:
dp[i][j] = 1
else:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
ans = max(ans, dp[i][j])
return ans * ans
Complexity
- ⏰ Time complexity:
O(m * n)wheremis the number of rows andnis the number of columns in the matrix. - 🧺 Space complexity:
O(m * n)for thedparray.
Method 2 - Top Down DP Using Recursion
Here is the approach:
- Recursive Approach: For each cell
(i, j)in the matrix, if it’s a ‘1’, then it could be part of a larger square. We need to check the three surrounding cells — top(i-1, j), left(i, j-1), and top-left(i-1, j-1)to determine the size of the square ending at(i, j). - Memoization: We use a 2D array
memoto store results of subproblems (i.e., the size of the largest square ending at each cell). Initially, this array is filled with-1to indicate uncomputed values. - Result Calculation: The result is the maximum square side length found in any cell, squared to get the area.
Code
Java
public int maximalSquare(char[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] memo = new int[m][n];
for(int i = 0; i< m; i++){
Arrays.fill(memo[i], -1);
}
int ans = 0;
for(int i = 0; i< m; i++){
for(int j = 0; j < n; j++){
ans = Math.max(ans, helper(matrix, i, j, memo));
}
}
return ans * ans;
}
private int helper(char[][] matrix,int i, int j, memo){
int m = matrix.length;
int n = matrix[0].length;
if(i >= m || j >= n || i < 0 || j < 0){
return 0;
}
if(memo[i][j] != -1){
return memo[i][j];
}
if(matrix[i][j] =='1'){
memo[i][j] = 1 + Math.min(helper(matrix, i -1, j - 1), Math.min(helper(matrix, i -1, j), helper(matrix, i, j - 1)));
}
return memo[i][j];
}
Python
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
def helper(i: int, j: int) -> int:
if i >= m or j >= n or i < 0 or j < 0:
return 0
if memo[i][j] != -1:
return memo[i][j]
if matrix[i][j] == '1':
memo[i][j] = 1 + min(helper(i - 1, j - 1), min(helper(i - 1, j), helper(i, j - 1)))
else:
memo[i][j] = 0
return memo[i][j]
m, n = len(matrix), len(matrix[0])
memo: List[List[int]] = [[-1] * n for _ in range(m)]
max_square_side = 0
for i in range(m):
for j in range(n):
max_square_side = max(max_square_side, helper(i, j))
return max_square_side * max_square_side
Complexity
- ⏰ Time complexity:
O(m*n) - 🧺 Space complexity:
O(m*n)