Problem

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.

Return that maximum distance to the closest person.

Examples

Example 1

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2020/09/10/distance.jpg)

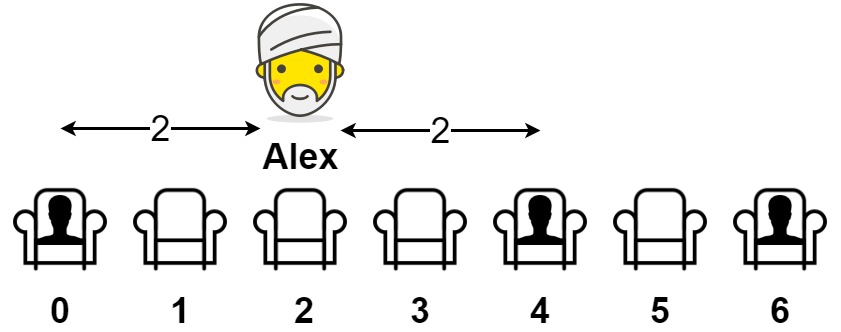
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation:
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2

1
2
3
4
5

Input: seats = [1,0,0,0]
Output: 3
Explanation:
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3

1
2

Input: seats = [0,1]
Output: 1

Constraints

  • 2 <= seats.length <= 2 * 10^4
  • seats[i] is 0 or 1.
  • At least one seat is empty.
  • At least one seat is occupied.

Solution

Method 1 – Linear Scan for Maximum Gap

Intuition

The largest distance to the closest person is determined by the largest block of empty seats between two people, or the empty seats at the start or end of the row. For each empty seat, the closest person is either to the left or right, so we want to maximize the minimum distance to a person.

Approach

  1. Scan from left to right, keeping track of the last occupied seat.
  2. For each empty seat, calculate the distance to the closest occupied seat on the left and right.
  3. For blocks at the start or end, the distance is the length of the block.
  4. The answer is the maximum of all these minimum distances.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
public:
    int maxDistToClosest(vector<int>& seats) {
        int n = seats.size(), ans = 0, last = -1;
        for (int i = 0; i < n; ++i) {
            if (seats[i] == 1) {
                if (last == -1) ans = i;
                else ans = max(ans, (i - last) / 2);
                last = i;
            }
        }
        ans = max(ans, n - 1 - last);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

func maxDistToClosest(seats []int) int {
    n, ans, last := len(seats), 0, -1
    for i := 0; i < n; i++ {
        if seats[i] == 1 {
            if last == -1 {
                ans = i
            } else {
                d := (i - last) / 2
                if d > ans {
                    ans = d
                }
            }
            last = i
        }
    }
    if n-1-last > ans {
        ans = n-1-last
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    public int maxDistToClosest(int[] seats) {
        int n = seats.length, ans = 0, last = -1;
        for (int i = 0; i < n; i++) {
            if (seats[i] == 1) {
                if (last == -1) ans = i;
                else ans = Math.max(ans, (i - last) / 2);
                last = i;
            }
        }
        ans = Math.max(ans, n - 1 - last);
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
    fun maxDistToClosest(seats: IntArray): Int {
        var ans = 0
        var last = -1
        for (i in seats.indices) {
            if (seats[i] == 1) {
                if (last == -1) ans = i
                else ans = maxOf(ans, (i - last) / 2)
                last = i
            }
        }
        ans = maxOf(ans, seats.size - 1 - last)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def maxDistToClosest(self, seats: list[int]) -> int:
        n = len(seats)
        ans = last = -1
        for i, v in enumerate(seats):
            if v == 1:
                if last == -1:
                    ans = i
                else:
                    ans = max(ans, (i - last) // 2)
                last = i
        ans = max(ans, n - 1 - last)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

impl Solution {
    pub fn max_dist_to_closest(seats: Vec<i32>) -> i32 {
        let n = seats.len();
        let mut ans = 0;
        let mut last = -1;
        for (i, &v) in seats.iter().enumerate() {
            if v == 1 {
                if last == -1 {
                    ans = i as i32;
                } else {
                    ans = ans.max(((i - last as usize) / 2) as i32);
                }
                last = i as i32;
            }
        }
        ans = ans.max((n as i32 - 1 - last) as i32);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    maxDistToClosest(seats: number[]): number {
        let n = seats.length, ans = 0, last = -1;
        for (let i = 0; i < n; i++) {
            if (seats[i] === 1) {
                if (last === -1) ans = i;
                else ans = Math.max(ans, Math.floor((i - last) / 2));
                last = i;
            }
        }
        ans = Math.max(ans, n - 1 - last);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n) — single pass through the array.
  • 🧺 Space complexity: O(1) — only a few variables are used.