Maximize Sum of Weights after Edge Removals

Problem

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi in the tree.

Your task is to remove zero or more edges such that:

• Each node has an edge with at most k other nodes, where k is given.
• The sum of the weights of the remaining edges is maximized.

Return the maximum possible sum of weights for the remaining edges after making the necessary removals.

Examples

Example 1

Input: edges = [[0,1,4],[0,2,2],[2,3,12],[2,4,6]], k = 2

Output: 22

Explanation:

![](https://assets.leetcode.com/uploads/2024/10/30/test1drawio.png)

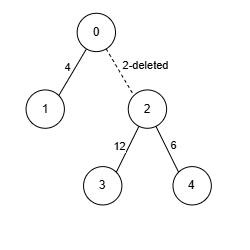
  * Node 2 has edges with 3 other nodes. We remove the edge `[0, 2, 2]`, ensuring that no node has edges with more than `k = 2` nodes.
  * The sum of weights is 22, and we can't achieve a greater sum. Thus, the answer is 22.

Example 2

Input: edges = [[0,1,5],[1,2,10],[0,3,15],[3,4,20],[3,5,5],[0,6,10]], k =
3

Output: 65

Explanation:

  * Since no node has edges connecting it to more than `k = 3` nodes, we don't remove any edges.
  * The sum of weights is 65. Thus, the answer is 65.

Constraints

• 2 <= n <= 10^5
• 1 <= k <= n - 1
• edges.length == n - 1
• edges[i].length == 3
• 0 <= edges[i][0] <= n - 1
• 0 <= edges[i][1] <= n - 1
• 1 <= edges[i][2] <= 10^6
• The input is generated such that edges form a valid tree.

Solution

Method 1 – Greedy DFS with Pruning

Intuition

To maximize the sum of edge weights while ensuring no node has more than k neighbors, we need to prune the smallest-weight edges from nodes with degree > k. Since the graph is a tree, we can use DFS to process each node, always keeping the k largest-weight edges at each node.

Approach

1. Build an adjacency list for the tree, storing (neighbor, weight) pairs.
2. Use DFS to traverse the tree from any node (e.g., node 0), keeping track of the parent to avoid revisiting.
3. For each node, collect the weights of all its child edges (excluding the parent).
4. If the number of child edges exceeds k, remove the smallest weights until only k remain.
5. The sum of the kept edges plus the best sums from the children is the answer for this subtree.
6. The answer is the sum for the root node.

Code

C++

class Solution {
public:
    int dfs(int u, int p, int k, vector<vector<pair<int,int>>>& g) {
        vector<int> childSums;
        for (auto& [v, w] : g[u]) {
            if (v == p) continue;
            int sub = dfs(v, u, k, g) + w;
            childSums.push_back(sub);
        }
        sort(childSums.rbegin(), childSums.rend());
        int ans = 0;
        for (int i = 0; i < min(k, (int)childSums.size()); ++i)
            ans += childSums[i];
        return ans;
    }
    int maximizeSumOfWeights(int n, vector<vector<int>>& edges, int k) {
        vector<vector<pair<int,int>>> g(n);
        for (auto& e : edges) {
            g[e[0]].emplace_back(e[1], e[2]);
            g[e[1]].emplace_back(e[0], e[2]);
        }
        return dfs(0, -1, k, g);
    }
};

Go

func maximizeSumOfWeights(n int, edges [][]int, k int) int {
    g := make([][]struct{v, w int}, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], struct{v, w int}{e[1], e[2]})
        g[e[1]] = append(g[e[1]], struct{v, w int}{e[0], e[2]})
    }
    var dfs func(u, p int) int
    dfs = func(u, p int) int {
        var childSums []int
        for _, e := range g[u] {
            if e.v == p { continue }
            sub := dfs(e.v, u) + e.w
            childSums = append(childSums, sub)
        }
        sort.Sort(sort.Reverse(sort.IntSlice(childSums)))
        ans := 0
        for i := 0; i < k && i < len(childSums); i++ {
            ans += childSums[i]
        }
        return ans
    }
    return dfs(0, -1)
}

Java

class Solution {
    public int maximizeSumOfWeights(int n, int[][] edges, int k) {
        List<int[]>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        return dfs(0, -1, k, g);
    }
    private int dfs(int u, int p, int k, List<int[]>[] g) {
        List<Integer> childSums = new ArrayList<>();
        for (int[] e : g[u]) {
            if (e[0] == p) continue;
            int sub = dfs(e[0], u, k, g) + e[1];
            childSums.add(sub);
        }
        childSums.sort(Collections.reverseOrder());
        int ans = 0;
        for (int i = 0; i < Math.min(k, childSums.size()); i++)
            ans += childSums.get(i);
        return ans;
    }
}

Kotlin

class Solution {
    fun maximizeSumOfWeights(n: Int, edges: Array<IntArray>, k: Int): Int {
        val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
        for (e in edges) {
            g[e[0]].add(e[1] to e[2])
            g[e[1]].add(e[0] to e[2])
        }
        fun dfs(u: Int, p: Int): Int {
            val childSums = mutableListOf<Int>()
            for ((v, w) in g[u]) {
                if (v == p) continue
                childSums.add(dfs(v, u) + w)
            }
            childSums.sortDescending()
            return childSums.take(k).sum()
        }
        return dfs(0, -1)
    }
}

Python

class Solution:
    def maximizeSumOfWeights(self, n: int, edges: list[list[int]], k: int) -> int:
        from collections import defaultdict
        g = defaultdict(list)
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        def dfs(u, p):
            child_sums = []
            for v, w in g[u]:
                if v == p:
                    continue
                child_sums.append(dfs(v, u) + w)
            child_sums.sort(reverse=True)
            return sum(child_sums[:k])
        return dfs(0, -1)

Rust

impl Solution {
    pub fn maximize_sum_of_weights(n: i32, edges: Vec<Vec<i32>>, k: i32) -> i32 {
        use std::collections::VecDeque;
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push((e[1] as usize, e[2]));
            g[e[1] as usize].push((e[0] as usize, e[2]));
        }
        fn dfs(u: usize, p: i32, k: usize, g: &Vec<Vec<(usize, i32)>>) -> i32 {
            let mut child_sums = vec![];
            for &(v, w) in &g[u] {
                if v as i32 == p { continue; }
                child_sums.push(dfs(v, u as i32, k, g) + w);
            }
            child_sums.sort_by(|a, b| b.cmp(a));
            child_sums.into_iter().take(k).sum()
        }
        dfs(0, -1, k as usize, &g)
    }
}

TypeScript

class Solution {
    maximizeSumOfWeights(n: number, edges: number[][], k: number): number {
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [u, v, w] of edges) {
            g[u].push([v, w]);
            g[v].push([u, w]);
        }
        function dfs(u: number, p: number): number {
            const childSums: number[] = [];
            for (const [v, w] of g[u]) {
                if (v === p) continue;
                childSums.push(dfs(v, u) + w);
            }
            childSums.sort((a, b) => b - a);
            return childSums.slice(0, k).reduce((a, b) => a + b, 0);
        }
        return dfs(0, -1);
    }
}

Complexity

• ⏰ Time complexity: O(n log k) — each node sorts at most its degree (≤ n), but only keeps top k.
• 🧺 Space complexity: O(n) — for the adjacency list and recursion stack.