Maximize the Distance Between Points on a Square
Problem
You are given an integer side, representing the edge length of a square with corners at (0, 0), (0, side), (side, 0), and (side, side) on a Cartesian plane.
You are also given a positive integer k and a 2D integer array points, where points[i] = [xi, yi] represents the coordinate of a point lying on the
boundary of the square.
You need to select k elements among points such that the minimum Manhattan distance between any two points is maximized.
Return the maximum possible minimum Manhattan distance between the selected k points.
The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi -xj| + |yi - yj|.
Examples
Example 1
Input: side = 2, points = [[0,2],[2,0],[2,2],[0,0]], k = 4
Output: 2
Explanation:
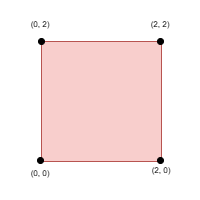
Select all four points.
Example 2
Input: side = 2, points = [[0,0],[1,2],[2,0],[2,2],[2,1]], k = 4
Output: 1
Explanation:
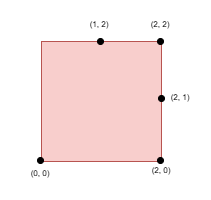
Select the points `(0, 0)`, `(2, 0)`, `(2, 2)`, and `(2, 1)`.
Example 3
Input: side = 2, points = [[0,0],[0,1],[0,2],[1,2],[2,0],[2,2],[2,1]], k =
5
Output: 1
Explanation:
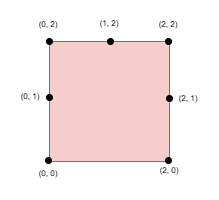
Select the points `(0, 0)`, `(0, 1)`, `(0, 2)`, `(1, 2)`, and `(2, 2)`.
Constraints
1 <= side <= 10^94 <= points.length <= min(4 * side, 15 * 103)points[i] == [xi, yi]- The input is generated such that:
points[i]lies on the boundary of the square.- All
points[i]are unique.
4 <= k <= min(25, points.length)
Solution
Method 1 – Binary Search with Greedy Placement
Intuition
To maximize the minimum Manhattan distance between any two selected points, we can use binary search on the answer. For each candidate distance, we greedily try to select points such that every new point is at least that far from all previously selected points.
Approach
- Map all points to a 1D representation of their position along the square's boundary (since all points are on the boundary, the Manhattan distance between two points is the distance along the boundary).
- Sort the mapped positions.
- Use binary search for the answer between 0 and the perimeter of the square.
- For each mid value, try to greedily select points such that each is at least
midaway from the previous selected point (wrapping around the perimeter if needed). - If possible to select
kpoints, try a larger value; otherwise, try smaller. - Return the largest value for which it is possible.
Code
C++
class Solution {
public:
int maximizeDistance(int side, vector<vector<int>>& points, int k) {
int n = points.size();
vector<int> pos;
int perim = 4 * side;
for (auto& p : points) {
int x = p[0], y = p[1];
if (y == 0) pos.push_back(x);
else if (x == side) pos.push_back(side + y);
else if (y == side) pos.push_back(3 * side - x);
else pos.push_back(4 * side - y);
}
sort(pos.begin(), pos.end());
int l = 0, r = perim, ans = 0;
while (l <= r) {
int m = (l + r) / 2;
int cnt = 1, last = pos[0];
for (int i = 1; i < n; ++i) {
if (pos[i] - last >= m) {
cnt++;
last = pos[i];
}
}
if (perim - last + pos[0] >= m) cnt++;
if (cnt >= k) { ans = m; l = m + 1; }
else r = m - 1;
}
return ans;
}
};
Go
func maximizeDistance(side int, points [][]int, k int) int {
n := len(points)
pos := make([]int, n)
perim := 4 * side
for i, p := range points {
x, y := p[0], p[1]
if y == 0 {
pos[i] = x
} else if x == side {
pos[i] = side + y
} else if y == side {
pos[i] = 3*side - x
} else {
pos[i] = 4*side - y
}
}
sort.Ints(pos)
l, r, ans := 0, perim, 0
for l <= r {
m := (l + r) / 2
cnt, last := 1, pos[0]
for i := 1; i < n; i++ {
if pos[i]-last >= m {
cnt++
last = pos[i]
}
}
if perim-last+pos[0] >= m {
cnt++
}
if cnt >= k {
ans = m
l = m + 1
} else {
r = m - 1
}
}
return ans
}
Java
class Solution {
public int maximizeDistance(int side, int[][] points, int k) {
int n = points.length, perim = 4 * side;
int[] pos = new int[n];
for (int i = 0; i < n; i++) {
int x = points[i][0], y = points[i][1];
if (y == 0) pos[i] = x;
else if (x == side) pos[i] = side + y;
else if (y == side) pos[i] = 3 * side - x;
else pos[i] = 4 * side - y;
}
Arrays.sort(pos);
int l = 0, r = perim, ans = 0;
while (l <= r) {
int m = (l + r) / 2, cnt = 1, last = pos[0];
for (int i = 1; i < n; i++) {
if (pos[i] - last >= m) {
cnt++;
last = pos[i];
}
}
if (perim - last + pos[0] >= m) cnt++;
if (cnt >= k) { ans = m; l = m + 1; }
else r = m - 1;
}
return ans;
}
}
Kotlin
class Solution {
fun maximizeDistance(side: Int, points: Array<IntArray>, k: Int): Int {
val n = points.size
val perim = 4 * side
val pos = IntArray(n)
for (i in 0 until n) {
val (x, y) = points[i]
pos[i] = when {
y == 0 -> x
x == side -> side + y
y == side -> 3 * side - x
else -> 4 * side - y
}
}
pos.sort()
var l = 0
var r = perim
var ans = 0
while (l <= r) {
val m = (l + r) / 2
var cnt = 1
var last = pos[0]
for (i in 1 until n) {
if (pos[i] - last >= m) {
cnt++
last = pos[i]
}
}
if (perim - last + pos[0] >= m) cnt++
if (cnt >= k) {
ans = m
l = m + 1
} else {
r = m - 1
}
}
return ans
}
}
Python
class Solution:
def maximizeDistance(self, side: int, points: list[list[int]], k: int) -> int:
n = len(points)
perim = 4 * side
pos = []
for x, y in points:
if y == 0:
pos.append(x)
elif x == side:
pos.append(side + y)
elif y == side:
pos.append(3 * side - x)
else:
pos.append(4 * side - y)
pos.sort()
l, r, ans = 0, perim, 0
while l <= r:
m = (l + r) // 2
cnt, last = 1, pos[0]
for i in range(1, n):
if pos[i] - last >= m:
cnt += 1
last = pos[i]
if perim - last + pos[0] >= m:
cnt += 1
if cnt >= k:
ans = m
l = m + 1
else:
r = m - 1
return ans
Rust
impl Solution {
pub fn maximize_distance(side: i32, points: Vec<Vec<i32>>, k: i32) -> i32 {
let n = points.len();
let perim = 4 * side;
let mut pos = vec![];
for p in &points {
let (x, y) = (p[0], p[1]);
pos.push(if y == 0 {
x
} else if x == side {
side + y
} else if y == side {
3 * side - x
} else {
4 * side - y
});
}
pos.sort();
let (mut l, mut r, mut ans) = (0, perim, 0);
while l <= r {
let m = (l + r) / 2;
let mut cnt = 1;
let mut last = pos[0];
for &p in pos.iter().skip(1) {
if p - last >= m {
cnt += 1;
last = p;
}
}
if perim - last + pos[0] >= m {
cnt += 1;
}
if cnt >= k {
ans = m;
l = m + 1;
} else {
r = m - 1;
}
}
ans
}
}
TypeScript
class Solution {
maximizeDistance(side: number, points: number[][], k: number): number {
const n = points.length, perim = 4 * side;
const pos: number[] = [];
for (const [x, y] of points) {
if (y === 0) pos.push(x);
else if (x === side) pos.push(side + y);
else if (y === side) pos.push(3 * side - x);
else pos.push(4 * side - y);
}
pos.sort((a, b) => a - b);
let l = 0, r = perim, ans = 0;
while (l <= r) {
const m = Math.floor((l + r) / 2);
let cnt = 1, last = pos[0];
for (let i = 1; i < n; i++) {
if (pos[i] - last >= m) {
cnt++;
last = pos[i];
}
}
if (perim - last + pos[0] >= m) cnt++;
if (cnt >= k) { ans = m; l = m + 1; }
else r = m - 1;
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n log P)— where n is the number of points and P is the perimeter. - 🧺 Space complexity:
O(n)— for storing mapped positions.