Maximum Average Subtree

Problem

Given the root of a binary tree, return the maximumaverage value of a subtree of that tree. Answers within 10-5 of the actual answer will be accepted.

A subtree of a tree is any node of that tree plus all its descendants.

The average value of a tree is the sum of its values, divided by the number of nodes.

Examples

Example 1:

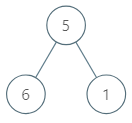
Input: root = [5,6,1]
Output: 6.00000
Explanation: 
For the node with value = 5 we have an average of (5 + 6 + 1) / 3 = 4.
For the node with value = 6 we have an average of 6 / 1 = 6.
For the node with value = 1 we have an average of 1 / 1 = 1.
So the answer is 6 which is the maximum.

Example 2:

Input: root = [0,null,1]
Output: 1.00000

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• 0 <= Node.val <= 10^5

Solution

Method 1 – DFS Postorder Traversal

Intuition

To find the maximum average of any subtree, we need to compute the sum and count of nodes for every subtree. A postorder DFS allows us to gather this information for each node, and we can update the maximum average as we traverse.

Approach

1. Define a helper function that returns the sum and count of nodes for a subtree rooted at a given node.
2. Traverse the tree in postorder (left, right, root).
3. For each node, calculate the average as sum/count and update the global maximum.
4. Return the maximum average found.

Code

C++

class Solution {
public:
    double maximumAverageSubtree(TreeNode* root) {
        double ans = 0;
        function<pair<int,int>(TreeNode*)> dfs = [&](TreeNode* node) -> pair<int,int> {
            if (!node) return {0, 0};
            auto [ls, lc] = dfs(node->left);
            auto [rs, rc] = dfs(node->right);
            int s = ls + rs + node->val;
            int c = lc + rc + 1;
            ans = max(ans, s * 1.0 / c);
            return {s, c};
        };
        dfs(root);
        return ans;
    }
};

Go

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}
func maximumAverageSubtree(root *TreeNode) float64 {
    ans := 0.0
    var dfs func(*TreeNode) (int, int)
    dfs = func(node *TreeNode) (int, int) {
        if node == nil { return 0, 0 }
        ls, lc := dfs(node.Left)
        rs, rc := dfs(node.Right)
        s := ls + rs + node.Val
        c := lc + rc + 1
        if avg := float64(s)/float64(c); avg > ans {
            ans = avg
        }
        return s, c
    }
    dfs(root)
    return ans
}

Java

class Solution {
    double ans = 0;
    public double maximumAverageSubtree(TreeNode root) {
        dfs(root);
        return ans;
    }
    private int[] dfs(TreeNode node) {
        if (node == null) return new int[]{0, 0};
        int[] l = dfs(node.left), r = dfs(node.right);
        int s = l[0] + r[0] + node.val;
        int c = l[1] + r[1] + 1;
        ans = Math.max(ans, s * 1.0 / c);
        return new int[]{s, c};
    }
}

Kotlin

class Solution {
    var ans = 0.0
    fun maximumAverageSubtree(root: TreeNode?): Double {
        fun dfs(node: TreeNode?): Pair<Int, Int> {
            if (node == null) return 0 to 0
            val (ls, lc) = dfs(node.left)
            val (rs, rc) = dfs(node.right)
            val s = ls + rs + node.`val`
            val c = lc + rc + 1
            ans = maxOf(ans, s.toDouble()/c)
            return s to c
        }
        dfs(root)
        return ans
    }
}

Python

class Solution:
    def maximumAverageSubtree(self, root: Optional[TreeNode]) -> float:
        self.ans = 0
        def dfs(node: Optional[TreeNode]) -> tuple[int, int]:
            if not node:
                return 0, 0
            ls, lc = dfs(node.left)
            rs, rc = dfs(node.right)
            s = ls + rs + node.val
            c = lc + rc + 1
            self.ans = max(self.ans, s / c)
            return s, c
        dfs(root)
        return self.ans

Rust

impl Solution {
    pub fn maximum_average_subtree(root: Option<Rc<RefCell<TreeNode>>>) -> f64 {
        fn dfs(node: Option<&Rc<RefCell<TreeNode>>>, ans: &mut f64) -> (i32, i32) {
            if let Some(n) = node {
                let n = n.borrow();
                let (ls, lc) = dfs(n.left.as_ref(), ans);
                let (rs, rc) = dfs(n.right.as_ref(), ans);
                let s = ls + rs + n.val;
                let c = lc + rc + 1;
                *ans = ans.max(&(s as f64 / c as f64));
                (s, c)
            } else {
                (0, 0)
            }
        }
        let mut ans = 0.0;
        dfs(root.as_ref(), &mut ans);
        ans
    }
}

TypeScript

class Solution {
    maximumAverageSubtree(root: TreeNode | null): number {
        let ans = 0;
        function dfs(node: TreeNode | null): [number, number] {
            if (!node) return [0, 0];
            const [ls, lc] = dfs(node.left);
            const [rs, rc] = dfs(node.right);
            const s = ls + rs + node.val;
            const c = lc + rc + 1;
            ans = Math.max(ans, s / c);
            return [s, c];
        }
        dfs(root);
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n), since we visit each node once.
• 🧺 Space complexity: O(h), where h is the height of the tree (recursion stack).