problemmediumalgorithmsleetcode-998leetcode 998leetcode998

Maximum Binary Tree II

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

A maximum tree is a tree where every node has a value greater than any other value in its subtree.

You are given the root of a maximum binary tree and an integer val.

Just as in the previous problem, the given tree was constructed from a list a (root = Construct(a)) recursively with the following Construct(a) routine:

  • If a is empty, return null.
  • Otherwise, let a[i] be the largest element of a. Create a root node with the value a[i].
  • The left child of root will be Construct([a[0], a[1], ..., a[i - 1]]).
  • The right child of root will be Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]).
  • Return root.

Note that we were not given a directly, only a root node root = Construct(a).

Suppose b is a copy of a with the value val appended to it. It is guaranteed that b has unique values.

Return Construct(b).

Examples

Example 1


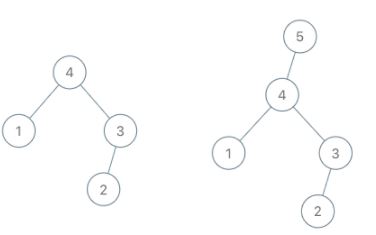
![](https://assets.leetcode.com/uploads/2021/08/09/maxtree1.JPG)

Input: root = [4,1,3,null,null,2], val = 5
Output: [5,4,null,1,3,null,null,2]
Explanation: a = [1,4,2,3], b = [1,4,2,3,5]

Example 2


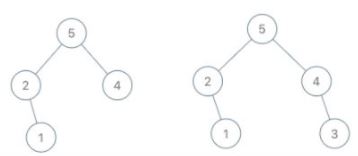
![](https://assets.leetcode.com/uploads/2021/08/09/maxtree21.JPG)

Input: root = [5,2,4,null,1], val = 3
Output: [5,2,4,null,1,null,3]
Explanation: a = [2,1,5,4], b = [2,1,5,4,3]

Example 3


![](https://assets.leetcode.com/uploads/2021/08/09/maxtree3.JPG)

Input: root = [5,2,3,null,1], val = 4
Output: [5,2,4,null,1,3]
Explanation: a = [2,1,5,3], b = [2,1,5,3,4]

Constraints

  • The number of nodes in the tree is in the range [1, 100].
  • 1 <= Node.val <= 100
  • All the values of the tree are unique.
  • 1 <= val <= 100

Solution

Method 1 – Recursive Insertion

Intuition

To insert a value into a maximum binary tree, we simulate appending the value to the end of the original array and reconstructing the tree. If the new value is greater than the root, it becomes the new root. Otherwise, we recursively insert it into the right subtree.

Approach

  1. If the root is null, return a new node with val.
  2. If val > root.val, create a new node with val as root and the old root as its left child.
  3. Otherwise, recursively insert val into the right subtree.
  4. Return the updated root.

Code

C++
class Solution {
public:
    TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
        if (!root) return new TreeNode(val);
        if (val > root->val) {
            TreeNode* node = new TreeNode(val);
            node->left = root;
            return node;
        }
        root->right = insertIntoMaxTree(root->right, val);
        return root;
    }
};
Go
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}
func insertIntoMaxTree(root *TreeNode, val int) *TreeNode {
    if root == nil {
        return &TreeNode{Val: val}
    }
    if val > root.Val {
        return &TreeNode{Val: val, Left: root}
    }
    root.Right = insertIntoMaxTree(root.Right, val)
    return root
}
Java
class Solution {
    public TreeNode insertIntoMaxTree(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        if (val > root.val) {
            TreeNode node = new TreeNode(val);
            node.left = root;
            return node;
        }
        root.right = insertIntoMaxTree(root.right, val);
        return root;
    }
}
Kotlin
class Solution {
    fun insertIntoMaxTree(root: TreeNode?, val_: Int): TreeNode? {
        if (root == null) return TreeNode(val_)
        if (val_ > root.`val`) {
            val node = TreeNode(val_)
            node.left = root
            return node
        }
        root.right = insertIntoMaxTree(root.right, val_)
        return root
    }
}
Python
class Solution:
    def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if not root:
            return TreeNode(val)
        if val > root.val:
            node = TreeNode(val)
            node.left = root
            return node
        root.right = self.insertIntoMaxTree(root.right, val)
        return root
Rust
impl Solution {
    pub fn insert_into_max_tree(root: Option<Rc<RefCell<TreeNode>>>, val: i32) -> Option<Rc<RefCell<TreeNode>>> {
        match root {
            None => Some(Rc::new(RefCell::new(TreeNode::new(val)))),
            Some(node) => {
                if val > node.borrow().val {
                    let mut new_node = TreeNode::new(val);
                    new_node.left = Some(node);
                    Some(Rc::new(RefCell::new(new_node)))
                } else {
                    let right = Solution::insert_into_max_tree(node.borrow_mut().right.take(), val);
                    node.borrow_mut().right = right;
                    Some(node)
                }
            }
        }
    }
}
TypeScript
class Solution {
    insertIntoMaxTree(root: TreeNode | null, val: number): TreeNode | null {
        if (!root) return new TreeNode(val);
        if (val > root.val) {
            const node = new TreeNode(val);
            node.left = root;
            return node;
        }
        root.right = this.insertIntoMaxTree(root.right, val);
        return root;
    }
}

Complexity

  • ⏰ Time complexity: O(h), where h is the height of the tree, since we only traverse the rightmost path.
  • 🧺 Space complexity: O(h), for the recursion stack.

Comments