Problem

A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.

You are also given an integer k. You are going on a trip that crosses exactly k highways. You may start at any city, but you may only visit each city at most once during your trip.

Return _themaximum cost of your trip. If there is no trip that meets the requirements, return _-1 .

Examples

Example 1:

1
2
3
4
5
6
7
8

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2247.Maximum%20Cost%20of%20Trip%20With%20K%20Highways/images/image-20220418173304-1.png)
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], k = 3
Output: 17
Explanation:
One possible trip is to go from 0 -> 1 -> 4 -> 3. The cost of this trip is 4 + 11 + 2 = 17.
Another possible trip is to go from 4 -> 1 -> 2 -> 3. The cost of this trip is 11 + 3 + 3 = 17.
It can be proven that 17 is the maximum possible cost of any valid trip.
Note that the trip 4 -> 1 -> 0 -> 1 is not allowed because you visit the city 1 twice.

Example 2:

1
2
3
4

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2247.Maximum%20Cost%20of%20Trip%20With%20K%20Highways/images/image-20220418173342-2.png)
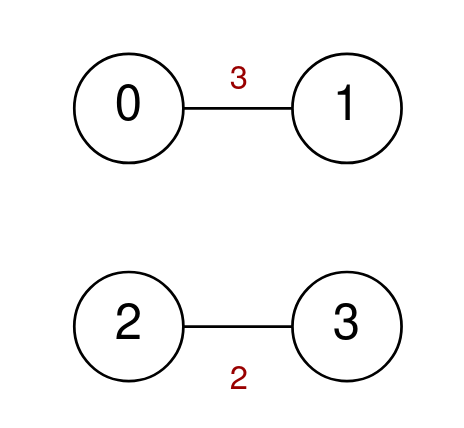
Input: n = 4, highways = [[0,1,3],[2,3,2]], k = 2
Output: -1
Explanation: There are no valid trips of length 2, so return -1.

Constraints:

  • 2 <= n <= 15
  • 1 <= highways.length <= 50
  • highways[i].length == 3
  • 0 <= city1i, city2i <= n - 1
  • city1i != city2i
  • 0 <= tolli <= 100
  • 1 <= k <= 50
  • There are no duplicate highways.

Solution

Method 1 – Bitmask Dynamic Programming

Intuition

Since the number of cities is small (≤ 15), we can use bitmask DP to track which cities have been visited. For each state (current city, visited cities, steps taken), we try all possible next cities via available highways, maximizing the total cost.

Approach

  1. Build an adjacency list for the graph with tolls.
  2. Use a DP table: dp[city][mask][steps] = max cost to reach city with mask visited and steps highways used.
  3. For each city as a starting point, initialize dp[start][1<<start][0] = 0.
  4. For each state, try all possible next cities via highways (if not visited), update DP for steps+1.
  5. After all, the answer is the maximum value among all dp[city][mask][k] for all cities and masks.
  6. If no valid trip, return -1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
public:
    int maximumCost(int n, vector<vector<int>>& highways, int k) {
        vector<vector<pair<int,int>>> g(n);
        for (auto& h : highways) {
            g[h[0]].push_back({h[1], h[2]});
            g[h[1]].push_back({h[0], h[2]});
        }
        int ans = -1;
        vector<vector<vector<int>>> dp(n, vector<vector<int>>(1<<n, vector<int>(k+1, -1)));
        for (int start = 0; start < n; ++start) dp[start][1<<start][0] = 0;
        for (int steps = 0; steps < k; ++steps) {
            for (int u = 0; u < n; ++u) {
                for (int mask = 0; mask < (1<<n); ++mask) {
                    if (dp[u][mask][steps] == -1) continue;
                    for (auto& [v, cost] : g[u]) {
                        if (!(mask & (1<<v))) {
                            int nmask = mask | (1<<v);
                            dp[v][nmask][steps+1] = max(dp[v][nmask][steps+1], dp[u][mask][steps] + cost);
                        }
                    }
                }
            }
        }
        for (int u = 0; u < n; ++u)
            for (int mask = 0; mask < (1<<n); ++mask)
                ans = max(ans, dp[u][mask][k]);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

func maximumCost(n int, highways [][]int, k int) int {
    g := make([][][2]int, n)
    for _, h := range highways {
        g[h[0]] = append(g[h[0]], [2]int{h[1], h[2]})
        g[h[1]] = append(g[h[1]], [2]int{h[0], h[2]})
    }
    dp := make([][][]int, n)
    for i := range dp {
        dp[i] = make([][]int, 1<<n)
        for j := range dp[i] {
            dp[i][j] = make([]int, k+1)
            for l := range dp[i][j] {
                dp[i][j][l] = -1
            }
        }
    }
    for start := 0; start < n; start++ {
        dp[start][1<<start][0] = 0
    }
    for steps := 0; steps < k; steps++ {
        for u := 0; u < n; u++ {
            for mask := 0; mask < (1 << n); mask++ {
                if dp[u][mask][steps] == -1 {
                    continue
                }
                for _, e := range g[u] {
                    v, cost := e[0], e[1]
                    if mask&(1<<v) == 0 {
                        nmask := mask | (1 << v)
                        if dp[v][nmask][steps+1] < dp[u][mask][steps]+cost {
                            dp[v][nmask][steps+1] = dp[u][mask][steps] + cost
                        }
                    }
                }
            }
        }
    }
    ans := -1
    for u := 0; u < n; u++ {
        for mask := 0; mask < (1 << n); mask++ {
            if dp[u][mask][k] > ans {
                ans = dp[u][mask][k]
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    public int maximumCost(int n, int[][] highways, int k) {
        List<int[]>[] g = new List[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] h : highways) {
            g[h[0]].add(new int[]{h[1], h[2]});
            g[h[1]].add(new int[]{h[0], h[2]});
        }
        int[][][] dp = new int[n][1<<n][k+1];
        for (int[][] arr2 : dp)
            for (int[] arr : arr2)
                Arrays.fill(arr, -1);
        for (int start = 0; start < n; start++) dp[start][1<<start][0] = 0;
        for (int steps = 0; steps < k; steps++) {
            for (int u = 0; u < n; u++) {
                for (int mask = 0; mask < (1<<n); mask++) {
                    if (dp[u][mask][steps] == -1) continue;
                    for (int[] e : g[u]) {
                        int v = e[0], cost = e[1];
                        if ((mask & (1<<v)) == 0) {
                            int nmask = mask | (1<<v);
                            dp[v][nmask][steps+1] = Math.max(dp[v][nmask][steps+1], dp[u][mask][steps] + cost);
                        }
                    }
                }
            }
        }
        int ans = -1;
        for (int u = 0; u < n; u++)
            for (int mask = 0; mask < (1<<n); mask++)
                ans = Math.max(ans, dp[u][mask][k]);
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
    fun maximumCost(n: Int, highways: Array<IntArray>, k: Int): Int {
        val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
        for (h in highways) {
            g[h[0]].add(h[1] to h[2])
            g[h[1]].add(h[0] to h[2])
        }
        val dp = Array(n) { Array(1 shl n) { IntArray(k+1) { -1 } } }
        for (start in 0 until n) dp[start][1 shl start][0] = 0
        for (steps in 0 until k) {
            for (u in 0 until n) {
                for (mask in 0 until (1 shl n)) {
                    if (dp[u][mask][steps] == -1) continue
                    for ((v, cost) in g[u]) {
                        if (mask and (1 shl v) == 0) {
                            val nmask = mask or (1 shl v)
                            dp[v][nmask][steps+1] = maxOf(dp[v][nmask][steps+1], dp[u][mask][steps] + cost)
                        }
                    }
                }
            }
        }
        var ans = -1
        for (u in 0 until n)
            for (mask in 0 until (1 shl n))
                ans = maxOf(ans, dp[u][mask][k])
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def maximumCost(self, n: int, highways: list[list[int]], k: int) -> int:
        from collections import defaultdict
        g = defaultdict(list)
        for u, v, cost in highways:
            g[u].append((v, cost))
            g[v].append((u, cost))
        dp = [[[-1] * (k+1) for _ in range(1<<n)] for _ in range(n)]
        for start in range(n):
            dp[start][1<<start][0] = 0
        for steps in range(k):
            for u in range(n):
                for mask in range(1<<n):
                    if dp[u][mask][steps] == -1:
                        continue
                    for v, cost in g[u]:
                        if not (mask & (1<<v)):
                            nmask = mask | (1<<v)
                            dp[v][nmask][steps+1] = max(dp[v][nmask][steps+1], dp[u][mask][steps] + cost)
        ans = -1
        for u in range(n):
            for mask in range(1<<n):
                ans = max(ans, dp[u][mask][k])
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

impl Solution {
    pub fn maximum_cost(n: i32, highways: Vec<Vec<i32>>, k: i32) -> i32 {
        let n = n as usize;
        let k = k as usize;
        let mut g = vec![vec![]; n];
        for h in highways {
            let (a, b, c) = (h[0] as usize, h[1] as usize, h[2]);
            g[a].push((b, c));
            g[b].push((a, c));
        }
        let mut dp = vec![vec![vec![-1; k+1]; 1<<n]; n];
        for start in 0..n {
            dp[start][1<<start][0] = 0;
        }
        for steps in 0..k {
            for u in 0..n {
                for mask in 0..(1<<n) {
                    if dp[u][mask][steps] == -1 { continue; }
                    for &(v, cost) in &g[u] {
                        if (mask & (1<<v)) == 0 {
                            let nmask = mask | (1<<v);
                            dp[v][nmask][steps+1] = dp[v][nmask][steps+1].max(dp[u][mask][steps] + cost);
                        }
                    }
                }
            }
        }
        let mut ans = -1;
        for u in 0..n {
            for mask in 0..(1<<n) {
                ans = ans.max(dp[u][mask][k]);
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    maximumCost(n: number, highways: number[][], k: number): number {
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [u, v, cost] of highways) {
            g[u].push([v, cost]);
            g[v].push([u, cost]);
        }
        const dp = Array.from({length: n}, () =>
            Array.from({length: 1 << n}, () => Array(k + 1).fill(-1))
        );
        for (let start = 0; start < n; start++) dp[start][1 << start][0] = 0;
        for (let steps = 0; steps < k; steps++) {
            for (let u = 0; u < n; u++) {
                for (let mask = 0; mask < (1 << n); mask++) {
                    if (dp[u][mask][steps] === -1) continue;
                    for (const [v, cost] of g[u]) {
                        if ((mask & (1 << v)) === 0) {
                            const nmask = mask | (1 << v);
                            dp[v][nmask][steps + 1] = Math.max(dp[v][nmask][steps + 1], dp[u][mask][steps] + cost);
                        }
                    }
                }
            }
        }
        let ans = -1;
        for (let u = 0; u < n; u++)
            for (let mask = 0; mask < (1 << n); mask++)
                ans = Math.max(ans, dp[u][mask][k]);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2 * 2^n * k), where n is the number of cities and k is the number of highways to use.
  • 🧺 Space complexity: O(n * 2^n * k), for the DP table.