Maximum Depth of Binary Tree

Problem

Given a binary tree, find its maximum depth.

Definition

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

The number of nodes along the longest path from the root node down to the farthest leaf node. Depth of root node is 0.

Examples

Example 1

graph TD;

A(3):::blue --- B(9):::blue & C(20):::blue
C --- D(15):::blue & E(7):::blue
classDef blue fill:#0000FF,stroke:#000,stroke-width:1px,color:#fff;

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2

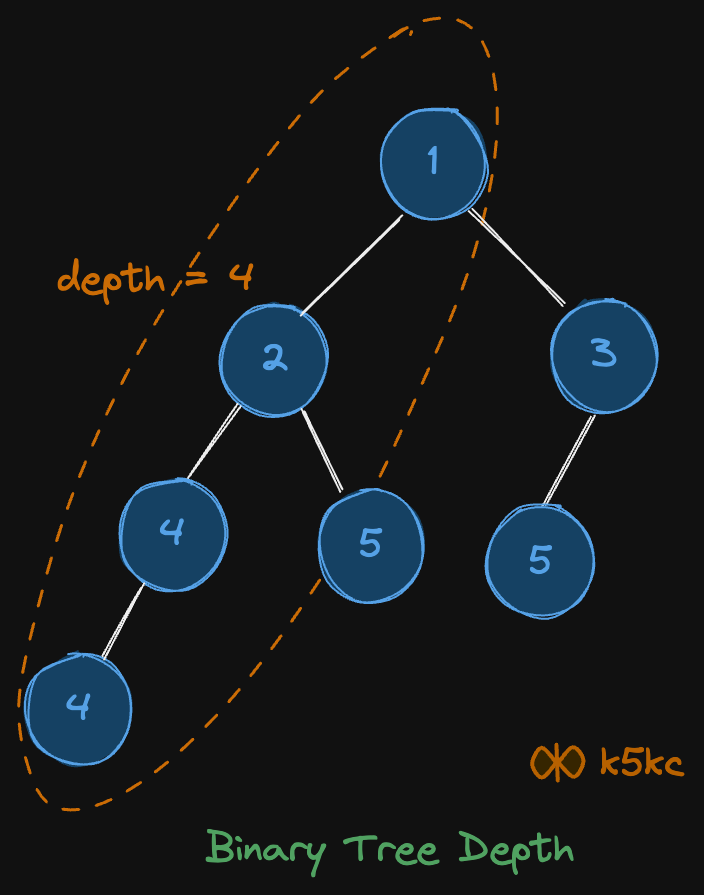
Input: root = [1, 2, 3, 4, 5, 5, null, 4]
Output: 4

Example 2

     1
   /    \
  2      3
 /  \   /  \
4    5 6    7

Input: root = [1, 2, 3, 4, 5, 6, 7]
Output: 3

Solution

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Video explanation

Here is the video explaining this method in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/gnRojSeXf14" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Recursive using Post order traversal

Intuition

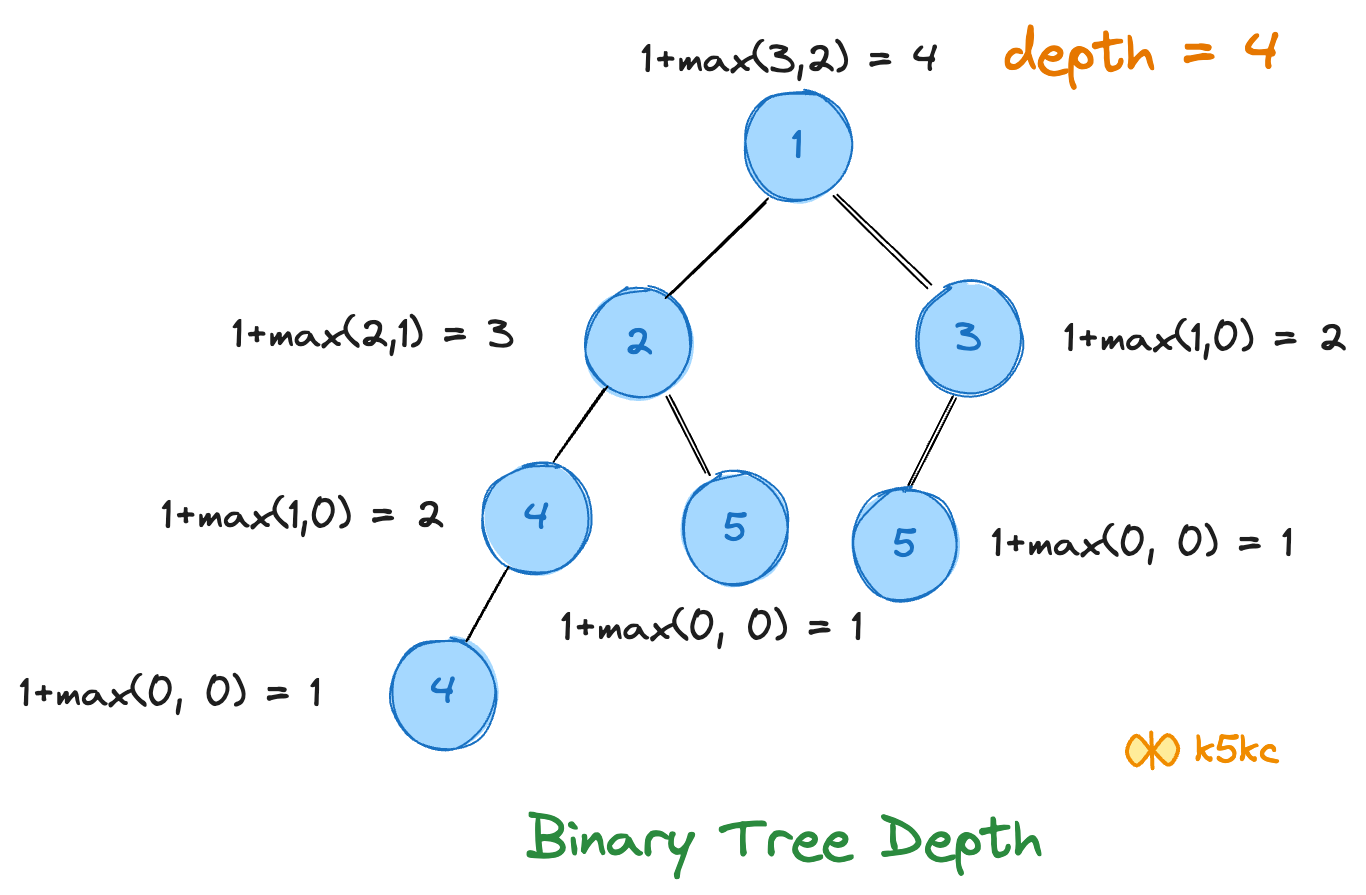
This is same as the number of nodes in the longest path. We can see that longest path with just one node is 1 i.e. the node itself. So, height aka max depth aka longest path is one more than the max of left or right sub tree height.

height(T) = max{height(T.left), height(T.right)}+1;

Approach

We can implement this with a top-down recursive function.

1. The base case for the recursion is a null node. If the node is null, it has no depth, so we return 0.
2. For any other node, we make two recursive calls: one to find the maximum depth of the left subtree, and another for the right subtree.
3. We take the max of the two depths returned by the children's subtrees and add 1 to it to account for the current node.
4. The final answer is the result of calling this function on the root of the tree.

Dry Run

Code

Java

public int maxDepth(TreeNode root) {
	if (root == null) {
		return 0;
	}

	int leftDepth = maxDepth(root.left);
	int rightDepth = maxDepth(root.right);

	return 1 + Math.max(leftDepth, rightDepth);
}

Python

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

Complexity

• ⏰ Time Complexity: O(n), where n is the number of nodes in the tree
• 🧺 Space Complexity: O(h), where h is the height of the tree (due to recursion stack; worst case O(n) for skewed tree)

Method 2 - Iterative DFS

Intuition

We can simulate the call-stack-based recursion of DFS with our own explicit stack. This avoids potential recursion depth limits and gives us direct control over the traversal. To find the maximum depth, we can't just store the nodes; we must also store their depth relative to the root. This turns the traversal into a search for the node with the highest depth value.

Approach

1. Create a stack to store pairs of (node, depth).
2. Initialize the stack by pushing the root node with a starting depth of 1.
3. Initialize a variable max_depth to 0 to track the maximum depth found so far.
4. Loop as long as the stack is not empty: a. Pop a (node, depth) pair from the stack. b. Update max_depth = max(max_depth, depth). c. If the node's children are not null, push them onto the stack with an incremented depth (depth + 1). To mimic a pre-order traversal, it's conventional to push the right child first, then the left.
5. Return max_depth.

Code

Java

Using Two Stacks

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Stack<TreeNode> nodeStack = new Stack<>();
        Stack<Integer> depthStack = new Stack<>();
        
        nodeStack.push(root);
        depthStack.push(1);
        
        int maxDepth = 0;
        
        while (!nodeStack.isEmpty()) {
            TreeNode currNode = nodeStack.pop();
            int currDepth = depthStack.pop();
            
            maxDepth = Math.max(maxDepth, currDepth);
            
            if (currNode.right != null) {
                nodeStack.push(currNode.right);
                depthStack.push(currDepth + 1);
            }
            if (currNode.left != null) {
                nodeStack.push(currNode.left);
                depthStack.push(currDepth + 1);
            }
        }
        return maxDepth;
    }
}

Using Pair Class

// Alternative using a helper class to store node-depth pairs
class Solution {
    private class Pair {
        TreeNode node;
        int depth;

        Pair(TreeNode node, int depth) {
            this.node = node;
            this.depth = depth;
        }
    }

    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Stack<Pair> stack = new Stack<>();
        stack.push(new Pair(root, 1));
        
        int maxDepth = 0;
        
        while (!stack.isEmpty()) {
            Pair current = stack.pop();
            TreeNode node = current.node;
            int depth = current.depth;
            
            maxDepth = Math.max(maxDepth, depth);
            
            if (node.right != null) {
                stack.push(new Pair(node.right, depth + 1));
            }
            if (node.left != null) {
                stack.push(new Pair(node.left, depth + 1));
            }
        }
        return maxDepth;
    }
}

Python

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        stack = [(root, 1)] # Python's tuple acts as a pair
        max_depth = 0
        
        while stack:
            node, depth = stack.pop()
            max_depth = max(max_depth, depth)
            
            if node.right:
                stack.append((node.right, depth + 1))
            if node.left:
                stack.append((node.left, depth + 1))
                
        return max_depth

Complexity

• ⏰ Time Complexity: O(n), where n is the number of nodes in the tree
• 🧺 Space Complexity: O(h), where h is the height of the tree (explicit stack; worst case O(n) for skewed tree)

Method 3 - Iterative Approach Using BFS

Intuition

We can also use [Binary Tree Traversal - Level Order](binary-tree-level-order-traversal) OR BFS to find max depth as well.

The maximum depth of a tree is simply the total number of levels it contains. A Breadth-First Search (BFS) is the perfect tool for this, as it naturally explores a tree one level at a time. By counting the number of levels we traverse, we can find the maximum depth.

Approach

1. Create a queue and add the root node to it.
2. Initialize a depth counter to 0.
3. Loop as long as the queue is not empty. This outer loop represents traversing one level at a time. a. Get the number of nodes on the current level (level_size). b. Create an inner loop that runs level_size times to ensure we only process nodes from the current level. c. In the inner loop, dequeue a node and enqueue its left and right children if they exist. d. After the inner loop finishes, we have completed a full level, so we increment the depth counter.
4. Once the queue is empty, depth will hold the total number of levels, which is the maximum depth.

Code

Java

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            for (int i = 0; i < levelSize; i++) {
                TreeNode curr = queue.poll();
                if (curr.left != null) {
                    queue.offer(curr.left);
                }
                if (curr.right != null) {
                    queue.offer(curr.right);
                }
            }
            depth++;
        }
        return depth;
    }
}

Python

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        queue = deque([root])
        depth = 0
        
        while queue:
            level_size = len(queue)
            for i in range(level_size):
                curr = queue.popleft()
                if curr.left:
                    queue.append(curr.left)
                if curr.right:
                    queue.append(curr.right)
            depth += 1
            
        return depth

Complexity

• ⏰ Time Complexity: O(n), where n is the number of nodes in the tree
• 🧺 Space Complexity: O(w), where w is the maximum width of the tree (worst case O(n) for a complete tree)