Problem

A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.

The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.

Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.

Examples

Example 1:

graph LR;
	0 --> 2
	1 --> 2
	2 --> 1
	3 --> 2
  

1
2
3
4
5
6
7

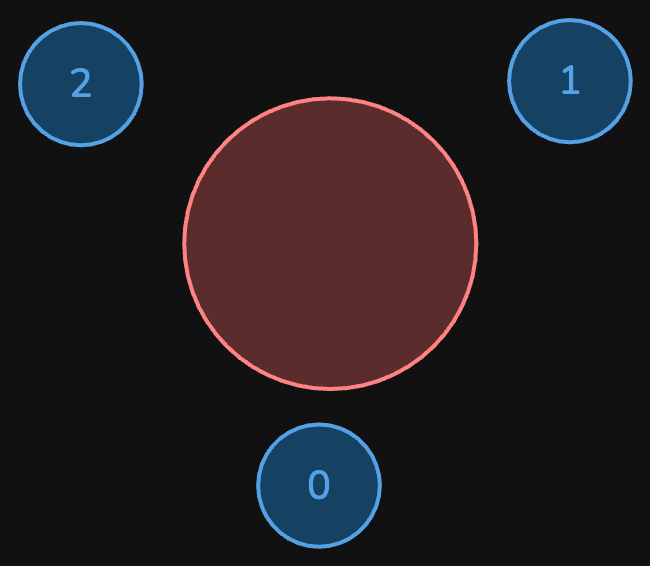
Input: favorite = [2,2,1,2]
Output: 3
Explanation:
The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table.
All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously.
Note that the company can also invite employees 1, 2, and 3, and give them their desired seats.
The maximum number of employees that can be invited to the meeting is 3.

Example 2:

graph LR;
0 --> 1
1 --> 2
2 --> 0
  
1
2
3
4
5
6
7
8
9

Input: favorite = [1,2,0]
Output: 3
Explanation: 
Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee.
The seating arrangement will be the same as that in the figure given in example 1:
- Employee 0 will sit between employees 2 and 1.
- Employee 1 will sit between employees 0 and 2.
- Employee 2 will sit between employees 1 and 0.
The maximum number of employees that can be invited to the meeting is 3.

Example 3:

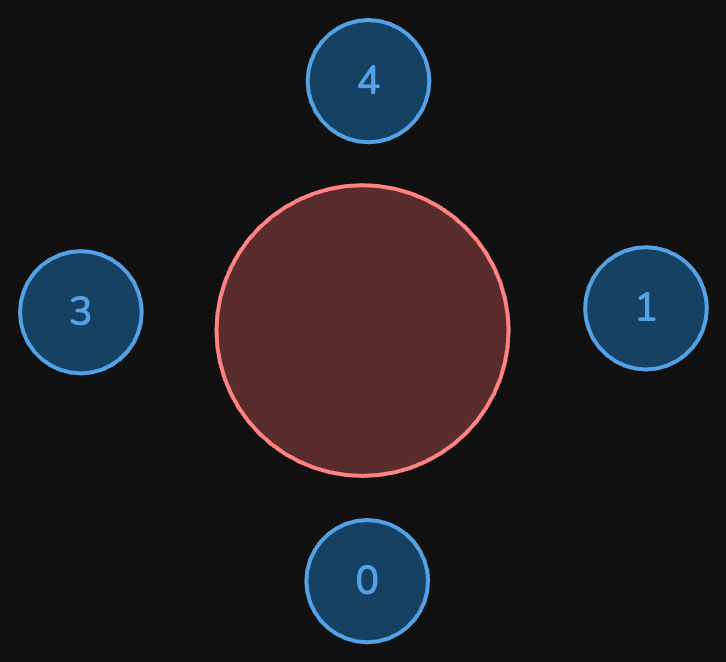
graph LR;
	0 --> 3
	1 --> 0
	2 --> 1
	3 --> 4
	4 --> 1
  
1
2
3
4
5
6
7

Input: favorite = [3,0,1,4,1]
Output: 4
Explanation:
The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table.
Employee 2 cannot be invited because the two spots next to their favorite employee 1 are taken.
So the company leaves them out of the meeting.
The maximum number of employees that can be invited to the meeting is 4.

Constraints:

  • n == favorite.length
  • 2 <= n <= 105
  • 0 <= favorite[i] <= n - 1
  • favorite[i] != i

Solution

Method 1 - Find the largest cycle

The key intuition is to treat employee favouritism as a directed graph problem where finding cycles is essential. In a meeting setup, cycles represent groups of employees that can sit next to each other seamlessly. Special attention to 2-cycles (mutual favourite pairs) allows us to extend seating by maximising possible chains leading into these pairs, thereby increasing the total number of employees who can be invited. The combined maximum of these cycles and chain extensions gives the optimal solution.

Approach

  1. Graph Representation:
    • We represent the relationships using a directed graph where favorite[i] implies a directed edge from employee i to the employee they favour.
  2. Detecting Cycles:
    • We traverse the graph to detect cycles using Depth First Search (DFS). Detecting cycles helps us understand which groups of people can indeed form a complete seating arrangement. For each cycle, we record its length.
    • A notable form of a cycle is the 2-cycle (mutual favourite pairs), where a pair of nodes point to each other. These 2-cycles need special consideration since additional employees can only be chained to these without breaking the cycle.
  3. Cycle Length Calculation:
    • During this detection, we identify the longest cycle (singleMaxCycleSize), which defines the maximum number of people that can be seated cyclically without considering the extension possibilities.
  4. Extending 2-Cycles:
    • For each 2-cycle detected, we explore possible chains leading into these cycles. This means, from each node of a 2-cycle, we use DFS to find the longest possible path that can be added to this cycle without violating the seating rules.
    • Depending on the chain length extending from both sides of the 2-cycle, we add these to the total count of employees that can be seated.
  5. Combining Results:
    • Finally, we compare the longest cycle length found with the longest possible setting considering the combined extensions of all 2-cycles. The maximum value between these gives us the desired result.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

class Solution {
    int N;
    Map<Integer, List<Integer>> graph = new HashMap<>();
    int singleMaxCycleSize = 0;
    List<int[]> pairs = new ArrayList<>();
    int[] favorite;
    
    public int maximumInvitations(int[] favorite) {
        this.favorite = favorite;
        N = favorite.length;
        for (int i = 0; i < favorite.length; i++) {
            int pre = favorite[i];
            int cur = i;
            graph.putIfAbsent(pre, new ArrayList<>());
            graph.get(pre).add(cur);
        }
        countCycle();
        return Math.max(singleMaxCycleSize, countSizeTwoExtra());
    }
    
    Map<Integer, Integer> maxLength = new HashMap<>();
    private int countSizeTwoExtra() {
        boolean[] visited = new boolean[N];
        int res = 0;
        for (int[] pair : pairs) {
            int a = pair[0];
            int b = pair[1];
            maxLength.put(a, 0);
            maxLength.put(b, 0);

            visited[a] = true;
            dfs(b, visited, 0, b);
            visited[a] = false;

            visited[b] = true;
            dfs(a, visited, 0, a);
            visited[b] = false;

            if (maxLength.get(a) > 0 && maxLength.get(b) > 0) {
                res += (maxLength.get(a) + maxLength.get(b));
            } else {
                res += Math.max(maxLength.get(a), maxLength.get(b));
            }
            res += 2;
        }
        return res;
    }
    
    private void dfs(int cur, boolean[] visited, int len, int start) {
        if (visited[cur]) return;
        maxLength.put(start, Math.max(maxLength.get(start), len));
        visited[cur] = true;
        for (int nei : graph.getOrDefault(cur, new ArrayList<>())) {
            if (!visited[nei]) dfs(nei, visited, len + 1, start);
        }
        visited[cur] = false;
    }
    
    private void countCycle() {
        boolean[] visited = new boolean[N];
        boolean[] recStack = new boolean[N];
        for (int i = 0; i < N; i++) {
            isCyclicUtil(i, visited, recStack, 0);
        }
    }
    
    private void isCyclicUtil(int i, boolean[] visited, boolean[] recStack, int count) {
        if (recStack[i]) {
            singleMaxCycleSize = Math.max(singleMaxCycleSize, count);
            if (count == 2) pairs.add(new int[] {i, favorite[i]});
            return;
        }
        if (visited[i]) return;
        visited[i] = true;
        recStack[i] = true;
        for (int child : graph.getOrDefault(i, new ArrayList<>())) {
            isCyclicUtil(child, visited, recStack, count + 1);
        }
        recStack[i] = false;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

class Solution:
    def maximumInvitations(self, favorite: List[int]) -> int:
        def dfs(cur: int, visited: Dict[int, bool], len: int, start: int) -> None:
            if visited[cur]:
                return
            max_lengths[start] = max(max_lengths[start], len)
            visited[cur] = True
            for nei in graph[cur]:
                if not visited[nei]:
                    dfs(nei, visited, len + 1, start)
            visited[cur] = False

        def find_cycles() -> None:
            visited = [False] * n
            rec_stack = [False] * n
            for i in range(n):
                if not visited[i]:
                    detect_cycle(i, visited, rec_stack, 0)
        
        def detect_cycle(i: int, visited: List[bool], rec_stack: List[bool], count: int) -> None:
            if rec_stack[i]:
                nonlocal single_max_cycle_size
                single_max_cycle_size = max(single_max_cycle_size, count)
                if count == 2:
                    pairs.append((i, favorite[i]))
                return
            if visited[i]:
                return
            visited[i] = True
            rec_stack[i] = True
            for child in graph[i]:
                detect_cycle(child, visited, rec_stack, count + 1)
            rec_stack[i] = False

        n = len(favorite)
        graph = defaultdict(list)
        for cur, pre in enumerate(favorite):
            graph[pre].append(cur)
        
        single_max_cycle_size = 0
        pairs = []
        find_cycles()
        
        max_lengths = defaultdict(int)
        max_extension_size = 0
        visited = [False] * n

        for a, b in pairs:
            visited[a] = True
            dfs(b, visited, 0, b)
            visited[a] = False

            visited[b] = True
            dfs(a, visited, 0, a)
            visited[b] = False

            if max_lengths[a] > 0 and max_lengths[b] > 0:
                max_extension_size += max_lengths[a] + max_lengths[b]
            else:
                max_extension_size += max(max_lengths[a], max_lengths[b])
            max_extension_size += 2
        
        return max(single_max_cycle_size, max_extension_size)

Complexity

  • ⏰ Time complexity: O(n), where n is the number of employees n, where each node (employee) and edge (relationship) is visited once during the graph traversal, detection of cycles, and exploration of possible extensions.
  • 🧺 Space complexity: O(n). Space complexity is also linear mainly due to:
    • The graph representation, which requires storage for nodes and their relations.
    • The additional structures such as visited arrays and dictionaries used to maintain states during DFS traversal and the extension calculations.