Problem

There is a rooted tree consisting of n nodes numbered 0 to n - 1. Each node’s number denotes its unique genetic value (i.e. the genetic value of node x is x). The genetic difference between two genetic values is defined as the **bitwise-**XOR of their values. You are given the integer array parents, where parents[i] is the parent for node i. If node x is the root of the tree, then parents[x] == -1.

You are also given the array queries where queries[i] = [nodei, vali]. For each query i, find the maximum genetic difference between vali and pi, where pi is the genetic value of any node that is on the path between nodei and the root (including nodei and the root). More formally, you want to maximize vali XOR pi.

Return an arrayans whereans[i]is the answer to theith query.

Examples

Example 1

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2021/06/29/c1.png)

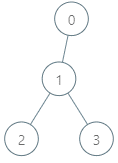
Input: parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]]
Output: [2,3,7]
Explanation: The queries are processed as follows:
- [0,2]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- [3,2]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- [2,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.

Example 2

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2021/06/29/c2.png)

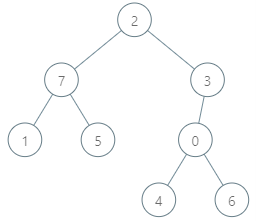
Input: parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]]
Output: [6,14,7]
Explanation: The queries are processed as follows:
- [4,6]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- [1,15]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- [0,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.

Constraints

  • 2 <= parents.length <= 10^5
  • 0 <= parents[i] <= parents.length - 1 for every node i that is not the root.
  • parents[root] == -1
  • 1 <= queries.length <= 3 * 10^4
  • 0 <= nodei <= parents.length - 1
  • 0 <= vali <= 2 * 10^5

Solution

Method 1 – Trie with DFS (Bitwise Trie)

Intuition

To answer each query efficiently, we need to find the maximum XOR of a given value with any node on the path from a given node to the root. Since the path is dynamic as we traverse the tree, we can use a Trie to store the current path’s node values and use DFS to traverse the tree. For each query at a node, we insert the node’s value into the Trie, answer the queries, and then remove the value as we backtrack.

Approach

  1. Build the tree from the parents array.
  2. For each node, keep a list of queries that need to be answered at that node.
  3. Use a Trie to store the current path’s node values.
  4. Perform DFS from the root:
    • Insert the current node’s value into the Trie.
    • For each query at this node, compute the maximum XOR with the query value using the Trie.
    • Recursively process all children.
    • Remove the current node’s value from the Trie when backtracking.
  5. Return the answers in the order of the queries.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

class TrieNode {
public:
    TrieNode* child[2] = {nullptr, nullptr};
    int cnt = 0;
};
class Solution {
public:
    vector<int> maxGeneticDifference(vector<int>& parents, vector<vector<int>>& queries) {
        int n = parents.size();
        vector<vector<int>> tree(n);
        int root = -1;
        for (int i = 0; i < n; ++i) {
            if (parents[i] == -1) root = i;
            else tree[parents[i]].push_back(i);
        }
        vector<vector<pair<int,int>>> qs(n);
        for (int i = 0; i < queries.size(); ++i) {
            int node = queries[i][0], val = queries[i][1];
            qs[node].push_back({val, i});
        }
        vector<int> ans(queries.size());
        TrieNode* trie = new TrieNode();
        function<void(int)> dfs = [&](int u) {
            insert(trie, u);
            for (auto& [val, idx] : qs[u]) {
                ans[idx] = query(trie, val);
            }
            for (int v : tree[u]) dfs(v);
            remove(trie, u);
        };
        dfs(root);
        return ans;
    }
    void insert(TrieNode* node, int x) {
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            if (!node->child[b]) node->child[b] = new TrieNode();
            node = node->child[b];
            node->cnt++;
        }
    }
    void remove(TrieNode* node, int x) {
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            node = node->child[b];
            node->cnt--;
        }
    }
    int query(TrieNode* node, int x) {
        int res = 0;
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            if (node->child[1-b] && node->child[1-b]->cnt > 0) {
                res |= (1 << i);
                node = node->child[1-b];
            } else {
                node = node->child[b];
            }
        }
        return res;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

type TrieNode struct {
    child [2]*TrieNode
    cnt   int
}
func maxGeneticDifference(parents []int, queries [][]int) []int {
    n := len(parents)
    tree := make([][]int, n)
    root := -1
    for i, p := range parents {
        if p == -1 {
            root = i
        } else {
            tree[p] = append(tree[p], i)
        }
    }
    qs := make([][][2]int, n)
    for i, q := range queries {
        node, val := q[0], q[1]
        qs[node] = append(qs[node], [2]int{val, i})
    }
    ans := make([]int, len(queries))
    trie := &TrieNode{}
    var insert func(*TrieNode, int)
    insert = func(node *TrieNode, x int) {
        for i := 17; i >= 0; i-- {
            b := (x >> i) & 1
            if node.child[b] == nil {
                node.child[b] = &TrieNode{}
            }
            node = node.child[b]
            node.cnt++
        }
    }
    var remove func(*TrieNode, int)
    remove = func(node *TrieNode, x int) {
        for i := 17; i >= 0; i-- {
            b := (x >> i) & 1
            node = node.child[b]
            node.cnt--
        }
    }
    var query func(*TrieNode, int) int
    query = func(node *TrieNode, x int) int {
        res := 0
        for i := 17; i >= 0; i-- {
            b := (x >> i) & 1
            if node.child[1-b] != nil && node.child[1-b].cnt > 0 {
                res |= 1 << i
                node = node.child[1-b]
            } else {
                node = node.child[b]
            }
        }
        return res
    }
    var dfs func(int)
    dfs = func(u int) {
        insert(trie, u)
        for _, q := range qs[u] {
            ans[q[1]] = query(trie, q[0])
        }
        for _, v := range tree[u] {
            dfs(v)
        }
        remove(trie, u)
    }
    dfs(root)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

class Solution {
    static class TrieNode {
        TrieNode[] child = new TrieNode[2];
        int cnt = 0;
    }
    public int[] maxGeneticDifference(int[] parents, int[][] queries) {
        int n = parents.length, root = -1;
        List<Integer>[] tree = new List[n];
        for (int i = 0; i < n; ++i) tree[i] = new ArrayList<>();
        for (int i = 0; i < n; ++i) {
            if (parents[i] == -1) root = i;
            else tree[parents[i]].add(i);
        }
        List<int[]>[] qs = new List[n];
        for (int i = 0; i < n; ++i) qs[i] = new ArrayList<>();
        for (int i = 0; i < queries.length; ++i) {
            int node = queries[i][0], val = queries[i][1];
            qs[node].add(new int[]{val, i});
        }
        int[] ans = new int[queries.length];
        TrieNode trie = new TrieNode();
        dfs(root, tree, qs, trie, ans);
        return ans;
    }
    void insert(TrieNode node, int x) {
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            if (node.child[b] == null) node.child[b] = new TrieNode();
            node = node.child[b];
            node.cnt++;
        }
    }
    void remove(TrieNode node, int x) {
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            node = node.child[b];
            node.cnt--;
        }
    }
    int query(TrieNode node, int x) {
        int res = 0;
        for (int i = 17; i >= 0; --i) {
            int b = (x >> i) & 1;
            if (node.child[1-b] != null && node.child[1-b].cnt > 0) {
                res |= 1 << i;
                node = node.child[1-b];
            } else {
                node = node.child[b];
            }
        }
        return res;
    }
    void dfs(int u, List<Integer>[] tree, List<int[]>[] qs, TrieNode trie, int[] ans) {
        insert(trie, u);
        for (int[] q : qs[u]) ans[q[1]] = query(trie, q[0]);
        for (int v : tree[u]) dfs(v, tree, qs, trie, ans);
        remove(trie, u);
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

class Solution {
    class TrieNode {
        val child = arrayOfNulls<TrieNode>(2)
        var cnt = 0
    }
    fun maxGeneticDifference(parents: IntArray, queries: Array<IntArray>): IntArray {
        val n = parents.size
        val tree = Array(n) { mutableListOf<Int>() }
        var root = -1
        for (i in 0 until n) {
            if (parents[i] == -1) root = i else tree[parents[i]].add(i)
        }
        val qs = Array(n) { mutableListOf<Pair<Int,Int>>() }
        for (i in queries.indices) {
            val (node, valq) = queries[i]
            qs[node].add(valq to i)
        }
        val ans = IntArray(queries.size)
        val trie = TrieNode()
        fun insert(x: Int) {
            var node = trie
            for (i in 17 downTo 0) {
                val b = (x shr i) and 1
                if (node.child[b] == null) node.child[b] = TrieNode()
                node = node.child[b]!!
                node.cnt++
            }
        }
        fun remove(x: Int) {
            var node = trie
            for (i in 17 downTo 0) {
                val b = (x shr i) and 1
                node = node.child[b]!!
                node.cnt--
            }
        }
        fun query(x: Int): Int {
            var node = trie
            var res = 0
            for (i in 17 downTo 0) {
                val b = (x shr i) and 1
                if (node.child[1-b] != null && node.child[1-b]!!.cnt > 0) {
                    res = res or (1 shl i)
                    node = node.child[1-b]!!
                } else {
                    node = node.child[b]!!
                }
            }
            return res
        }
        fun dfs(u: Int) {
            insert(u)
            for ((valq, idx) in qs[u]) ans[idx] = query(valq)
            for (v in tree[u]) dfs(v)
            remove(u)
        }
        dfs(root)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

class Solution:
    class TrieNode:
        def __init__(self):
            self.child = [None, None]
            self.cnt = 0
    def maxGeneticDifference(self, parents: list[int], queries: list[list[int]]) -> list[int]:
        n = len(parents)
        tree = [[] for _ in range(n)]
        root = -1
        for i, p in enumerate(parents):
            if p == -1:
                root = i
            else:
                tree[p].append(i)
        qs = [[] for _ in range(n)]
        for idx, (node, val) in enumerate(queries):
            qs[node].append((val, idx))
        ans = [0] * len(queries)
        trie = self.TrieNode()
        def insert(x: int):
            node = trie
            for i in range(17, -1, -1):
                b = (x >> i) & 1
                if not node.child[b]:
                    node.child[b] = self.TrieNode()
                node = node.child[b]
                node.cnt += 1
        def remove(x: int):
            node = trie
            for i in range(17, -1, -1):
                b = (x >> i) & 1
                node = node.child[b]
                node.cnt -= 1
        def query(x: int) -> int:
            node = trie
            res = 0
            for i in range(17, -1, -1):
                b = (x >> i) & 1
                if node.child[1-b] and node.child[1-b].cnt > 0:
                    res |= 1 << i
                    node = node.child[1-b]
                else:
                    node = node.child[b]
            return res
        def dfs(u: int):
            insert(u)
            for val, idx in qs[u]:
                ans[idx] = query(val)
            for v in tree[u]:
                dfs(v)
            remove(u)
        dfs(root)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

impl Solution {
    pub fn max_genetic_difference(parents: Vec<i32>, queries: Vec<Vec<i32>>) -> Vec<i32> {
        use std::collections::VecDeque;
        struct TrieNode {
            child: [Option<Box<TrieNode>>; 2],
            cnt: i32,
        }
        impl TrieNode {
            fn new() -> Self {
                TrieNode { child: [None, None], cnt: 0 }
            }
        }
        let n = parents.len();
        let mut tree = vec![vec![]; n];
        let mut root = 0;
        for (i, &p) in parents.iter().enumerate() {
            if p == -1 {
                root = i;
            } else {
                tree[p as usize].push(i);
            }
        }
        let mut qs = vec![vec![]; n];
        for (idx, q) in queries.iter().enumerate() {
            qs[q[0] as usize].push((q[1], idx));
        }
        let mut ans = vec![0; queries.len()];
        let mut trie = TrieNode::new();
        fn insert(trie: &mut TrieNode, x: i32) {
            let mut node = trie;
            for i in (0..=17).rev() {
                let b = ((x >> i) & 1) as usize;
                if node.child[b].is_none() {
                    node.child[b] = Some(Box::new(TrieNode::new()));
                }
                node = node.child[b].as_mut().unwrap();
                node.cnt += 1;
            }
        }
        fn remove(trie: &mut TrieNode, x: i32) {
            let mut node = trie;
            for i in (0..=17).rev() {
                let b = ((x >> i) & 1) as usize;
                node = node.child[b].as_mut().unwrap();
                node.cnt -= 1;
            }
        }
        fn query(trie: &TrieNode, x: i32) -> i32 {
            let mut node = trie;
            let mut res = 0;
            for i in (0..=17).rev() {
                let b = ((x >> i) & 1) as usize;
                if node.child[1-b].is_some() && node.child[1-b].as_ref().unwrap().cnt > 0 {
                    res |= 1 << i;
                    node = node.child[1-b].as_ref().unwrap();
                } else {
                    node = node.child[b].as_ref().unwrap();
                }
            }
            res
        }
        fn dfs(u: usize, tree: &Vec<Vec<usize>>, qs: &Vec<Vec<(i32, usize)>>, trie: &mut TrieNode, ans: &mut Vec<i32>) {
            insert(trie, u as i32);
            for &(val, idx) in &qs[u] {
                ans[idx] = query(trie, val);
            }
            for &v in &tree[u] {
                dfs(v, tree, qs, trie, ans);
            }
            remove(trie, u as i32);
        }
        dfs(root, &tree, &qs, &mut trie, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

class TrieNode {
    child: [TrieNode | null, TrieNode | null] = [null, null];
    cnt = 0;
}
class Solution {
    maxGeneticDifference(parents: number[], queries: number[][]): number[] {
        const n = parents.length;
        const tree: number[][] = Array.from({length: n}, () => []);
        let root = -1;
        for (let i = 0; i < n; ++i) {
            if (parents[i] === -1) root = i;
            else tree[parents[i]].push(i);
        }
        const qs: [number, number][][] = Array.from({length: n}, () => []);
        for (let i = 0; i < queries.length; ++i) {
            const [node, val] = queries[i];
            qs[node].push([val, i]);
        }
        const ans: number[] = Array(queries.length).fill(0);
        const trie = new TrieNode();
        function insert(x: number) {
            let node = trie;
            for (let i = 17; i >= 0; --i) {
                const b = (x >> i) & 1;
                if (!node.child[b]) node.child[b] = new TrieNode();
                node = node.child[b]!;
                node.cnt++;
            }
        }
        function remove(x: number) {
            let node = trie;
            for (let i = 17; i >= 0; --i) {
                const b = (x >> i) & 1;
                node = node.child[b]!;
                node.cnt--;
            }
        }
        function query(x: number): number {
            let node = trie, res = 0;
            for (let i = 17; i >= 0; --i) {
                const b = (x >> i) & 1;
                if (node.child[1-b] && node.child[1-b]!.cnt > 0) {
                    res |= 1 << i;
                    node = node.child[1-b]!;
                } else {
                    node = node.child[b]!;
                }
            }
            return res;
        }
        function dfs(u: number) {
            insert(u);
            for (const [val, idx] of qs[u]) ans[idx] = query(val);
            for (const v of tree[u]) dfs(v);
            remove(u);
        }
        dfs(root);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O((n + q) * log M), where n is the number of nodes, q is the number of queries, and M is the maximum value (up to 2e5). Each insert, remove, and query operation on the Trie takes O(log M) time.
  • 🧺 Space complexity: O(n * log M), for the Trie and auxiliary structures.