Maximum Good People Based on Statements
Problem
There are two types of persons:
- The good person : The person who always tells the truth.
- The bad person : The person who might tell the truth and might lie.
You are given a 0-indexed 2D integer array statements of size n x n
that represents the statements made by n people about each other. More specifically, statements[i][j] could be one of the following:
0which represents a statement made by personithat personjis a bad person.1which represents a statement made by personithat personjis a good person.2represents that no statement is made by personiabout personj.
Additionally, no person ever makes a statement about themselves. Formally, we have that statements[i][i] = 2 for all 0 <= i < n.
Return _themaximum number of people who can be good based on the statements made by the _n people.
Examples
Example 1
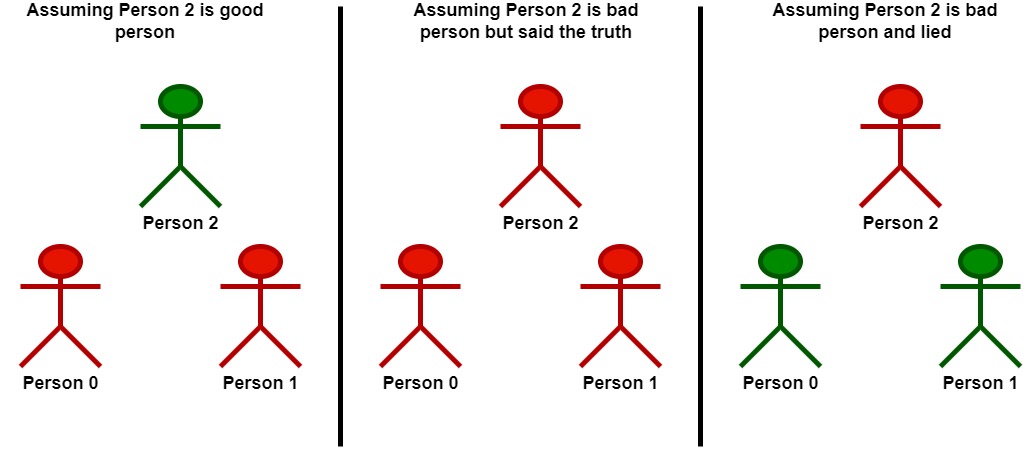
Input: statements = [[2,1,2],[1,2,2],[2,0,2]]
Output: 2
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is good.
- Person 1 states that person 0 is good.
- Person 2 states that person 1 is bad.
Let's take person 2 as the key.
- Assuming that person 2 is a good person:
- Based on the statement made by person 2, person 1 is a bad person.
- Now we know for sure that person 1 is bad and person 2 is good.
- Based on the statement made by person 1, and since person 1 is bad, they could be:
- telling the truth. There will be a contradiction in this case and this assumption is invalid.
- lying. In this case, person 0 is also a bad person and lied in their statement.
- **Following that person 2 is a good person, there will be only one good person in the group**.
- Assuming that person 2 is a bad person:
- Based on the statement made by person 2, and since person 2 is bad, they could be:
- telling the truth. Following this scenario, person 0 and 1 are both bad as explained before.
- **Following that person 2 is bad but told the truth, there will be no good persons in the group**.
- lying. In this case person 1 is a good person.
- Since person 1 is a good person, person 0 is also a good person.
- **Following that person 2 is bad and lied, there will be two good persons in the group**.
We can see that at most 2 persons are good in the best case, so we return 2.
Note that there is more than one way to arrive at this conclusion.
Example 2
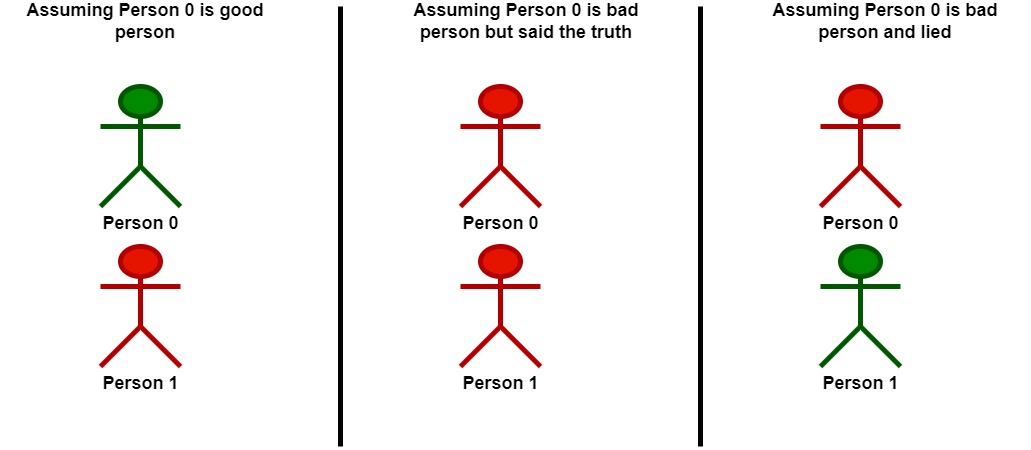
Input: statements = [[2,0],[0,2]]
Output: 1
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is bad.
- Person 1 states that person 0 is bad.
Let's take person 0 as the key.
- Assuming that person 0 is a good person:
- Based on the statement made by person 0, person 1 is a bad person and was lying.
- **Following that person 0 is a good person, there will be only one good person in the group**.
- Assuming that person 0 is a bad person:
- Based on the statement made by person 0, and since person 0 is bad, they could be:
- telling the truth. Following this scenario, person 0 and 1 are both bad.
- **Following that person 0 is bad but told the truth, there will be no good persons in the group**.
- lying. In this case person 1 is a good person.
- **Following that person 0 is bad and lied, there will be only one good person in the group**.
We can see that at most, one person is good in the best case, so we return 1.
Note that there is more than one way to arrive at this conclusion.
Constraints
n == statements.length == statements[i].length2 <= n <= 15statements[i][j]is either0,1, or2.statements[i][i] == 2
Solution
Method 1 – Bitmask Enumeration
Intuition
Since the number of people n is small (≤15), we can try every possible combination of who is good and who is bad using bitmasking. For each combination, we check if it is valid: every good person must tell the truth, so their statements must match the assignment. We maximize the number of good people among all valid assignments.
Approach
- Let n be the number of people. For each bitmask from 0 to 2^n - 1:
- The i-th bit is 1 if person i is good, 0 if bad.
- For each bitmask, check if it is valid:
- For every person i marked as good, check all their statements:
- If statements[i][j] == 2, skip.
- If statements[i][j] == 1, person j must be good in the bitmask.
- If statements[i][j] == 0, person j must be bad in the bitmask.
- If all good people's statements are consistent, update the answer with the number of good people in this bitmask.
- For every person i marked as good, check all their statements:
- Return the maximum number of good people found.
Code
C++
class Solution {
public:
int maximumGood(vector<vector<int>>& statements) {
int n = statements.size(), ans = 0;
for (int mask = 0; mask < (1 << n); ++mask) {
bool valid = true;
for (int i = 0; i < n && valid; ++i) {
if (!((mask >> i) & 1)) continue;
for (int j = 0; j < n; ++j) {
if (statements[i][j] == 2) continue;
if (statements[i][j] != ((mask >> j) & 1)) {
valid = false;
break;
}
}
}
if (valid) ans = max(ans, __builtin_popcount(mask));
}
return ans;
}
};
Go
func maximumGood(statements [][]int) int {
n, ans := len(statements), 0
for mask := 0; mask < 1<<n; mask++ {
valid := true
for i := 0; i < n && valid; i++ {
if (mask>>i)&1 == 0 {
continue
}
for j := 0; j < n; j++ {
if statements[i][j] == 2 {
continue
}
if statements[i][j] != ((mask>>j)&1) {
valid = false
break
}
}
}
if valid {
cnt := 0
for x := mask; x > 0; x &= x - 1 {
cnt++
}
if cnt > ans {
ans = cnt
}
}
}
return ans
}
Java
class Solution {
public int maximumGood(int[][] statements) {
int n = statements.length, ans = 0;
for (int mask = 0; mask < (1 << n); ++mask) {
boolean valid = true;
for (int i = 0; i < n && valid; ++i) {
if (((mask >> i) & 1) == 0) continue;
for (int j = 0; j < n; ++j) {
if (statements[i][j] == 2) continue;
if (statements[i][j] != ((mask >> j) & 1)) {
valid = false;
break;
}
}
}
if (valid) ans = Math.max(ans, Integer.bitCount(mask));
}
return ans;
}
}
Kotlin
class Solution {
fun maximumGood(statements: Array<IntArray>): Int {
val n = statements.size
var ans = 0
for (mask in 0 until (1 shl n)) {
var valid = true
for (i in 0 until n) {
if ((mask shr i) and 1 == 0) continue
for (j in 0 until n) {
if (statements[i][j] == 2) continue
if (statements[i][j] != ((mask shr j) and 1)) {
valid = false
break
}
}
if (!valid) break
}
if (valid) ans = maxOf(ans, mask.countOneBits())
}
return ans
}
}
Python
class Solution:
def maximumGood(self, statements: list[list[int]]) -> int:
n = len(statements)
ans = 0
for mask in range(1 << n):
valid = True
for i in range(n):
if not (mask >> i) & 1:
continue
for j in range(n):
if statements[i][j] == 2:
continue
if statements[i][j] != ((mask >> j) & 1):
valid = False
break
if not valid:
break
if valid:
ans = max(ans, bin(mask).count('1'))
return ans
Rust
impl Solution {
pub fn maximum_good(statements: Vec<Vec<i32>>) -> i32 {
let n = statements.len();
let mut ans = 0;
for mask in 0..(1 << n) {
let mut valid = true;
for i in 0..n {
if (mask >> i) & 1 == 0 { continue; }
for j in 0..n {
if statements[i][j] == 2 { continue; }
if statements[i][j] != ((mask >> j) & 1) as i32 {
valid = false;
break;
}
}
if !valid { break; }
}
if valid {
ans = ans.max(mask.count_ones() as i32);
}
}
ans
}
}
TypeScript
class Solution {
maximumGood(statements: number[][]): number {
const n = statements.length;
let ans = 0;
for (let mask = 0; mask < (1 << n); ++mask) {
let valid = true;
for (let i = 0; i < n && valid; ++i) {
if (((mask >> i) & 1) === 0) continue;
for (let j = 0; j < n; ++j) {
if (statements[i][j] === 2) continue;
if (statements[i][j] !== ((mask >> j) & 1)) {
valid = false;
break;
}
}
}
if (valid) ans = Math.max(ans, mask.toString(2).split('1').length - 1);
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n * 2^n), since we check all possible assignments (2^n) and for each, check all n^2 statements. - 🧺 Space complexity:
O(1), only a few variables are used for computation.