Problem

You are given two integers red and blue representing the count of red and blue colored balls. You have to arrange these balls to form a triangle such that the 1st row will have 1 ball, the 2nd row will have 2 balls, the 3rd row will have 3 balls, and so on.

All the balls in a particular row should be the same color, and adjacent rows should have different colors.

Return the maximum height of the triangle that can be achieved.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


Input: red = 2, blue = 4

Output: 3

Explanation:

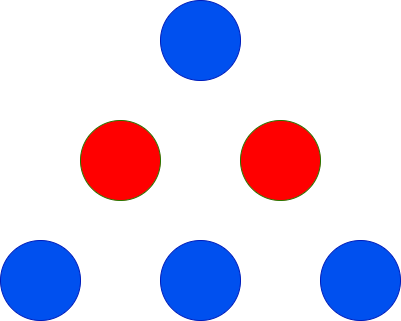
![](https://assets.leetcode.com/uploads/2024/06/16/brb.png)

The only possible arrangement is shown above.

Example 2

1
2
3
4
5
6
7
8
9


Input: red = 2, blue = 1

Output: 2

Explanation:

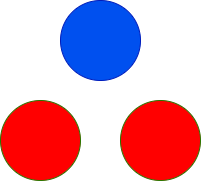
![](https://assets.leetcode.com/uploads/2024/06/16/br.png)  
The only possible arrangement is shown above.

Example 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


Input: red = 1, blue = 1

Output: 1

#### Example 4

Input: red = 10, blue = 1

Output: 2

Explanation:

![](https://assets.leetcode.com/uploads/2024/06/16/br.png)  
The only possible arrangement is shown above.

Constraints

  • 1 <= red, blue <= 100

Solution

Method 1 – Greedy Alternating Rows

Intuition

To maximize the triangle’s height, we should always use the color with more balls for the larger rows. By alternating colors for each row and always picking the color with more balls for the next row, we can build the tallest triangle possible.

Approach

  1. Start with height = 0, and let the current color be the one with more balls.
  2. For each row (starting from 1), check if the current color has enough balls for the row.
  3. If yes, subtract the row size from that color, increment height, and switch to the other color for the next row.
  4. Repeat until you can’t build the next row.
  5. Return the final height.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int maximumHeight(int red, int blue) {
        int h = 0, cur = red >= blue ? 0 : 1;
        int cnt[2] = {red, blue};
        while (cnt[cur] >= h + 1) {
            cnt[cur] -= h + 1;
            h++;
            cur ^= 1;
        }
        return h;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func maximumHeight(red int, blue int) int {
    h := 0
    cur := 0
    cnt := [2]int{red, blue}
    if blue > red {
        cur = 1
    }
    for cnt[cur] >= h+1 {
        cnt[cur] -= h + 1
        h++
        cur ^= 1
    }
    return h
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
    public int maximumHeight(int red, int blue) {
        int h = 0, cur = red >= blue ? 0 : 1;
        int[] cnt = {red, blue};
        while (cnt[cur] >= h + 1) {
            cnt[cur] -= h + 1;
            h++;
            cur ^= 1;
        }
        return h;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    fun maximumHeight(red: Int, blue: Int): Int {
        var h = 0
        var cur = if (red >= blue) 0 else 1
        val cnt = intArrayOf(red, blue)
        while (cnt[cur] >= h + 1) {
            cnt[cur] -= h + 1
            h++
            cur = cur xor 1
        }
        return h
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def maximumHeight(self, red: int, blue: int) -> int:
        h = 0
        cur = 0 if red >= blue else 1
        cnt = [red, blue]
        while cnt[cur] >= h + 1:
            cnt[cur] -= h + 1
            h += 1
            cur ^= 1
        return h
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

impl Solution {
    pub fn maximum_height(red: i32, blue: i32) -> i32 {
        let mut h = 0;
        let mut cur = if red >= blue { 0 } else { 1 };
        let mut cnt = [red, blue];
        while cnt[cur] >= h + 1 {
            cnt[cur] -= h + 1;
            h += 1;
            cur ^= 1;
        }
        h
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
    maximumHeight(red: number, blue: number): number {
        let h = 0, cur = red >= blue ? 0 : 1;
        const cnt = [red, blue];
        while (cnt[cur] >= h + 1) {
            cnt[cur] -= h + 1;
            h++;
            cur ^= 1;
        }
        return h;
    }
}

Complexity

  • ⏰ Time complexity: O(sqrt(n)), where n = red + blue, since the number of rows grows quadratically with the number of balls.
  • 🧺 Space complexity: O(1), only a few variables are used.