Maximum Non Negative Product in a Matrix

Problem

You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative, return -1.

Notice that the modulo is performed after getting the maximum product.

Examples

Example 1

1
2
3


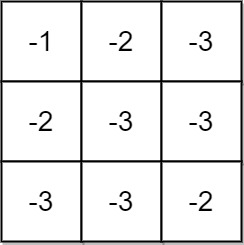
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
Output: -1
Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.

Example 2

1
2
3


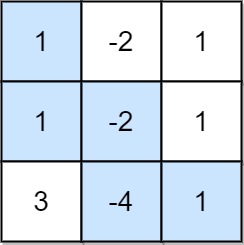
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).

Example 3

1
2
3


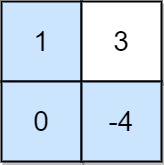
Input: grid = [[1,3],[0,-4]]
Output: 0
Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).

Solution

Method 1 – Dynamic Programming (Track Min and Max Product)

Intuition

At each cell, keep track of both the maximum and minimum product that can be achieved to reach that cell, since multiplying by a negative can flip the sign. The answer is the maximum non-negative product at the bottom-right cell.

Approach

Use two DP tables: max_dp[i][j] and min_dp[i][j] for the max/min product to reach cell (i, j).
For each cell, consider coming from the left or above, and update both max and min using the current cell value.
At the end, if the maximum product at the bottom-right is negative, return -1; otherwise, return it modulo 1e9+7.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution {
public:
    int maxProductPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), MOD = 1e9+7;
        vector<vector<long>> max_dp(m, vector<long>(n)), min_dp(m, vector<long>(n));
        max_dp[0][0] = min_dp[0][0] = grid[0][0];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 && j == 0) continue;
                long mx = LONG_MIN, mn = LONG_MAX;
                if (i > 0) {
                    mx = max(mx, max_dp[i-1][j] * grid[i][j]);
                    mx = max(mx, min_dp[i-1][j] * grid[i][j]);
                    mn = min(mn, max_dp[i-1][j] * grid[i][j]);
                    mn = min(mn, min_dp[i-1][j] * grid[i][j]);
                }
                if (j > 0) {
                    mx = max(mx, max_dp[i][j-1] * grid[i][j]);
                    mx = max(mx, min_dp[i][j-1] * grid[i][j]);
                    mn = min(mn, max_dp[i][j-1] * grid[i][j]);
                    mn = min(mn, min_dp[i][j-1] * grid[i][j]);
                }
                max_dp[i][j] = mx;
                min_dp[i][j] = mn;
            }
        }
        long res = max_dp[m-1][n-1];
        return res < 0 ? -1 : res % MOD;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


func maxProductPath(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    mod := int(1e9+7)
    maxDp := make([][]int64, m)
    minDp := make([][]int64, m)
    for i := range maxDp {
        maxDp[i] = make([]int64, n)
        minDp[i] = make([]int64, n)
    }
    maxDp[0][0], minDp[0][0] = int64(grid[0][0]), int64(grid[0][0])
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if i == 0 && j == 0 { continue }
            mx, mn := int64(-1<<63), int64(1<<63-1)
            if i > 0 {
                mx = max(mx, maxDp[i-1][j]*int64(grid[i][j]))
                mx = max(mx, minDp[i-1][j]*int64(grid[i][j]))
                mn = min(mn, maxDp[i-1][j]*int64(grid[i][j]))
                mn = min(mn, minDp[i-1][j]*int64(grid[i][j]))
            }
            if j > 0 {
                mx = max(mx, maxDp[i][j-1]*int64(grid[i][j]))
                mx = max(mx, minDp[i][j-1]*int64(grid[i][j]))
                mn = min(mn, maxDp[i][j-1]*int64(grid[i][j]))
                mn = min(mn, minDp[i][j-1]*int64(grid[i][j]))
            }
            maxDp[i][j], minDp[i][j] = mx, mn
        }
    }
    res := maxDp[m-1][n-1]
    if res < 0 { return -1 }
    return int(res % int64(mod))
}
func max(a, b int64) int64 { if a > b { return a } else { return b } }
func min(a, b int64) int64 { if a < b { return a } else { return b } }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


class Solution {
    public int maxProductPath(int[][] grid) {
        int m = grid.length, n = grid[0].length, MOD = 1_000_000_007;
        long[][] maxDp = new long[m][n], minDp = new long[m][n];
        maxDp[0][0] = minDp[0][0] = grid[0][0];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 && j == 0) continue;
                long mx = Long.MIN_VALUE, mn = Long.MAX_VALUE;
                if (i > 0) {
                    mx = Math.max(mx, maxDp[i-1][j] * grid[i][j]);
                    mx = Math.max(mx, minDp[i-1][j] * grid[i][j]);
                    mn = Math.min(mn, maxDp[i-1][j] * grid[i][j]);
                    mn = Math.min(mn, minDp[i-1][j] * grid[i][j]);
                }
                if (j > 0) {
                    mx = Math.max(mx, maxDp[i][j-1] * grid[i][j]);
                    mx = Math.max(mx, minDp[i][j-1] * grid[i][j]);
                    mn = Math.min(mn, maxDp[i][j-1] * grid[i][j]);
                    mn = Math.min(mn, minDp[i][j-1] * grid[i][j]);
                }
                maxDp[i][j] = mx;
                minDp[i][j] = mn;
            }
        }
        long res = maxDp[m-1][n-1];
        return res < 0 ? -1 : (int)(res % MOD);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
    fun maxProductPath(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        val MOD = 1_000_000_007L
        val maxDp = Array(m) { LongArray(n) }
        val minDp = Array(m) { LongArray(n) }
        maxDp[0][0] = grid[0][0].toLong()
        minDp[0][0] = grid[0][0].toLong()
        for (i in 0 until m) {
            for (j in 0 until n) {
                if (i == 0 && j == 0) continue
                var mx = Long.MIN_VALUE
                var mn = Long.MAX_VALUE
                if (i > 0) {
                    mx = maxOf(mx, maxDp[i-1][j] * grid[i][j])
                    mx = maxOf(mx, minDp[i-1][j] * grid[i][j])
                    mn = minOf(mn, maxDp[i-1][j] * grid[i][j])
                    mn = minOf(mn, minDp[i-1][j] * grid[i][j])
                }
                if (j > 0) {
                    mx = maxOf(mx, maxDp[i][j-1] * grid[i][j])
                    mx = maxOf(mx, minDp[i][j-1] * grid[i][j])
                    mn = minOf(mn, maxDp[i][j-1] * grid[i][j])
                    mn = minOf(mn, minDp[i][j-1] * grid[i][j])
                }
                maxDp[i][j] = mx
                minDp[i][j] = mn
            }
        }
        val res = maxDp[m-1][n-1]
        return if (res < 0) -1 else (res % MOD).toInt()
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution:
    def maxProductPath(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        MOD = 10**9+7
        max_dp = [[0]*n for _ in range(m)]
        min_dp = [[0]*n for _ in range(m)]
        max_dp[0][0] = min_dp[0][0] = grid[0][0]
        for i in range(m):
            for j in range(n):
                if i == 0 and j == 0: continue
                mx, mn = float('-inf'), float('inf')
                if i > 0:
                    mx = max(mx, max_dp[i-1][j]*grid[i][j], min_dp[i-1][j]*grid[i][j])
                    mn = min(mn, max_dp[i-1][j]*grid[i][j], min_dp[i-1][j]*grid[i][j])
                if j > 0:
                    mx = max(mx, max_dp[i][j-1]*grid[i][j], min_dp[i][j-1]*grid[i][j])
                    mn = min(mn, max_dp[i][j-1]*grid[i][j], min_dp[i][j-1]*grid[i][j])
                max_dp[i][j] = mx
                min_dp[i][j] = mn
        res = max_dp[m-1][n-1]
        return -1 if res < 0 else res % MOD

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


impl Solution {
    pub fn max_product_path(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut max_dp = vec![vec![0i64; n]; m];
        let mut min_dp = vec![vec![0i64; n]; m];
        max_dp[0][0] = grid[0][0] as i64;
        min_dp[0][0] = grid[0][0] as i64;
        for i in 0..m {
            for j in 0..n {
                if i == 0 && j == 0 { continue; }
                let mut mx = i64::MIN;
                let mut mn = i64::MAX;
                if i > 0 {
                    mx = mx.max(max_dp[i-1][j] * grid[i][j] as i64);
                    mx = mx.max(min_dp[i-1][j] * grid[i][j] as i64);
                    mn = mn.min(max_dp[i-1][j] * grid[i][j] as i64);
                    mn = mn.min(min_dp[i-1][j] * grid[i][j] as i64);
                }
                if j > 0 {
                    mx = mx.max(max_dp[i][j-1] * grid[i][j] as i64);
                    mx = mx.max(min_dp[i][j-1] * grid[i][j] as i64);
                    mn = mn.min(max_dp[i][j-1] * grid[i][j] as i64);
                    mn = mn.min(min_dp[i][j-1] * grid[i][j] as i64);
                }
                max_dp[i][j] = mx;
                min_dp[i][j] = mn;
            }
        }
        let res = max_dp[m-1][n-1];
        if res < 0 { -1 } else { (res % 1_000_000_007) as i32 }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution {
    maxProductPath(grid: number[][]): number {
        const m = grid.length, n = grid[0].length, MOD = 1e9+7;
        const maxDp: number[][] = Array.from({length: m}, () => Array(n).fill(0));
        const minDp: number[][] = Array.from({length: m}, () => Array(n).fill(0));
        maxDp[0][0] = minDp[0][0] = grid[0][0];
        for (let i = 0; i < m; ++i) {
            for (let j = 0; j < n; ++j) {
                if (i === 0 && j === 0) continue;
                let mx = -Infinity, mn = Infinity;
                if (i > 0) {
                    mx = Math.max(mx, maxDp[i-1][j] * grid[i][j], minDp[i-1][j] * grid[i][j]);
                    mn = Math.min(mn, maxDp[i-1][j] * grid[i][j], minDp[i-1][j] * grid[i][j]);
                }
                if (j > 0) {
                    mx = Math.max(mx, maxDp[i][j-1] * grid[i][j], minDp[i][j-1] * grid[i][j]);
                    mn = Math.min(mn, maxDp[i][j-1] * grid[i][j], minDp[i][j-1] * grid[i][j]);
                }
                maxDp[i][j] = mx;
                minDp[i][j] = mn;
            }
        }
        const res = maxDp[m-1][n-1];
        return res < 0 ? -1 : res % MOD;
    }
}

Complexity

⏰ Time complexity: O(m * n)
- Each cell is visited once, and we do constant work per cell.
🧺 Space complexity: O(m * n)
- Two DP tables of size m x n are used.

Problem#

Examples#

Example 1#

Example 2#

Example 3#

Solution#

Method 1 – Dynamic Programming (Track Min and Max Product)#

Intuition#

Approach#

Code#

Complexity#