Maximum Number of Achievable Transfer Requests Problem

Problem

We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It’s transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [fromi, toi] represents an employee’s request to transfer from building fromi to building toi.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

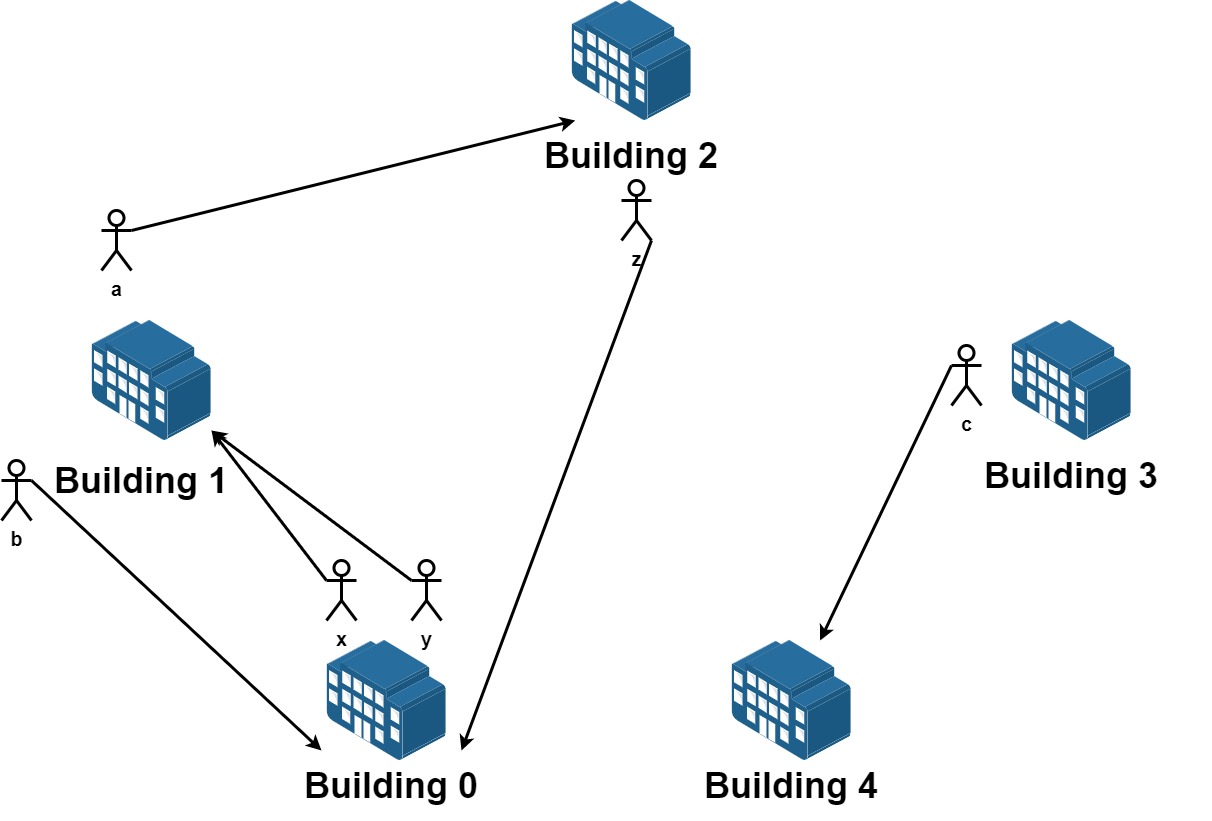
Input:
n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output:
 5
**Explantion:** Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

1
2
3
4
5
6
7
8
9

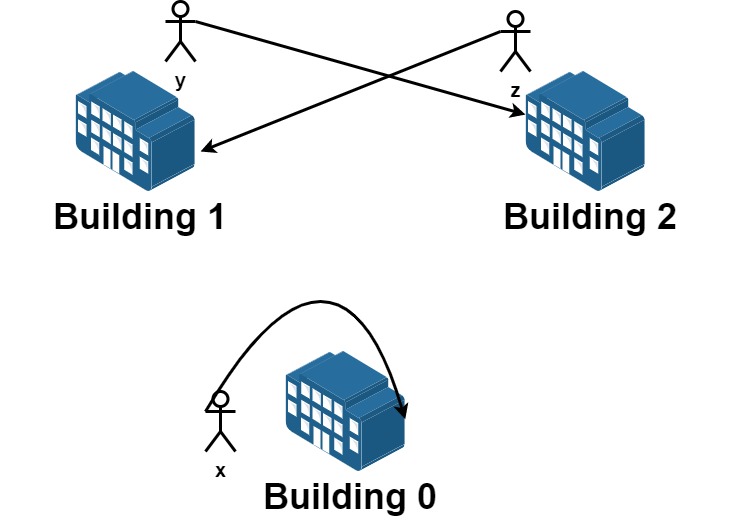
Input:
n = 3, requests = [[0,0],[1,2],[2,1]]
Output:
 3
**Explantion:** Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.

Example 3:

1
2
3
4

Input:
n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output:
 4

Solution

Method 1 – Backtracking with State Validation

Intuition

We want the largest set of requests such that the net change for each building is zero. Since the number of requests is small, we can use backtracking to try all possible subsets and check if the net change is zero for each building.

Approach

  1. For each subset of requests, use backtracking to include or exclude each request.
  2. Track the net change for each building in an array.
  3. If all net changes are zero, update the answer with the size of the subset.
  4. Try all combinations and return the largest valid subset size.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    int ans = 0;
    void dfs(int i, int n, vector<vector<int>>& req, vector<int>& bal, int cnt) {
        if (i == req.size()) {
            if (all_of(bal.begin(), bal.end(), [](int x){return x==0;}))
                ans = max(ans, cnt);
            return;
        }
        dfs(i+1, n, req, bal, cnt);
        bal[req[i][0]]--;
        bal[req[i][1]]++;
        dfs(i+1, n, req, bal, cnt+1);
        bal[req[i][0]]++;
        bal[req[i][1]]--;
    }
    int maximumRequests(int n, vector<vector<int>>& requests) {
        vector<int> bal(n);
        dfs(0, n, requests, bal, 0);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

func maximumRequests(n int, requests [][]int) int {
    ans := 0
    var dfs func(i int, bal []int, cnt int)
    dfs = func(i int, bal []int, cnt int) {
        if i == len(requests) {
            ok := true
            for _, v := range bal {
                if v != 0 { ok = false }
            }
            if ok && cnt > ans { ans = cnt }
            return
        }
        dfs(i+1, bal, cnt)
        bal[requests[i][0]]--
        bal[requests[i][1]]++
        dfs(i+1, bal, cnt+1)
        bal[requests[i][0]]++
        bal[requests[i][1]]--
    }
    bal := make([]int, n)
    dfs(0, bal, 0)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    int ans = 0;
    public int maximumRequests(int n, int[][] requests) {
        int[] bal = new int[n];
        dfs(0, n, requests, bal, 0);
        return ans;
    }
    void dfs(int i, int n, int[][] req, int[] bal, int cnt) {
        if (i == req.length) {
            for (int v : bal) if (v != 0) return;
            ans = Math.max(ans, cnt);
            return;
        }
        dfs(i+1, n, req, bal, cnt);
        bal[req[i][0]]--;
        bal[req[i][1]]++;
        dfs(i+1, n, req, bal, cnt+1);
        bal[req[i][0]]++;
        bal[req[i][1]]--;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    var ans = 0
    fun maximumRequests(n: Int, requests: Array<IntArray>): Int {
        val bal = IntArray(n)
        dfs(0, n, requests, bal, 0)
        return ans
    }
    fun dfs(i: Int, n: Int, req: Array<IntArray>, bal: IntArray, cnt: Int) {
        if (i == req.size) {
            if (bal.all { it == 0 }) ans = maxOf(ans, cnt)
            return
        }
        dfs(i+1, n, req, bal, cnt)
        bal[req[i][0]]--
        bal[req[i][1]]++
        dfs(i+1, n, req, bal, cnt+1)
        bal[req[i][0]]++
        bal[req[i][1]]--
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def maximumRequests(n: int, requests: list[list[int]]) -> int:
    ans = 0
    def dfs(i: int, bal: list[int], cnt: int):
        nonlocal ans
        if i == len(requests):
            if all(x == 0 for x in bal):
                ans = max(ans, cnt)
            return
        dfs(i+1, bal, cnt)
        bal[requests[i][0]] -= 1
        bal[requests[i][1]] += 1
        dfs(i+1, bal, cnt+1)
        bal[requests[i][0]] += 1
        bal[requests[i][1]] -= 1
    dfs(0, [0]*n, 0)
    return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

impl Solution {
    pub fn maximum_requests(n: i32, requests: Vec<Vec<i32>>) -> i32 {
        fn dfs(i: usize, bal: &mut [i32], cnt: i32, req: &Vec<Vec<i32>>, ans: &mut i32) {
            if i == req.len() {
                if bal.iter().all(|&x| x == 0) {
                    *ans = (*ans).max(cnt);
                }
                return;
            }
            dfs(i+1, bal, cnt, req, ans);
            bal[req[i][0] as usize] -= 1;
            bal[req[i][1] as usize] += 1;
            dfs(i+1, bal, cnt+1, req, ans);
            bal[req[i][0] as usize] += 1;
            bal[req[i][1] as usize] -= 1;
        }
        let mut ans = 0;
        let mut bal = vec![0; n as usize];
        dfs(0, &mut bal, 0, &requests, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    ans = 0;
    maximumRequests(n: number, requests: number[][]): number {
        const bal = Array(n).fill(0);
        this.dfs(0, n, requests, bal, 0);
        return this.ans;
    }
    dfs(i: number, n: number, req: number[][], bal: number[], cnt: number): void {
        if (i === req.length) {
            if (bal.every(x => x === 0)) this.ans = Math.max(this.ans, cnt);
            return;
        }
        this.dfs(i+1, n, req, bal, cnt);
        bal[req[i][0]]--;
        bal[req[i][1]]++;
        this.dfs(i+1, n, req, bal, cnt+1);
        bal[req[i][0]]++;
        bal[req[i][1]]--;
    }
}

Complexity

  • ⏰ Time complexity: O(2^m * n), where m is the number of requests and n is the number of buildings.
  • 🧺 Space complexity: O(n + m), for recursion stack and balance array.