Maximum Number of Events That Can Be Attended II

Problem

You are given an array of events where events[i] = [startDayi, endDayi, valuei]. The ith event starts at startDayi and ends at endDayi, and if you attend this event, you will receive a value of valuei. You are also given an integer k which represents the maximum number of events you can attend.

You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.

Return the maximum sum of values that you can receive by attending events.

Examples

Example 1:

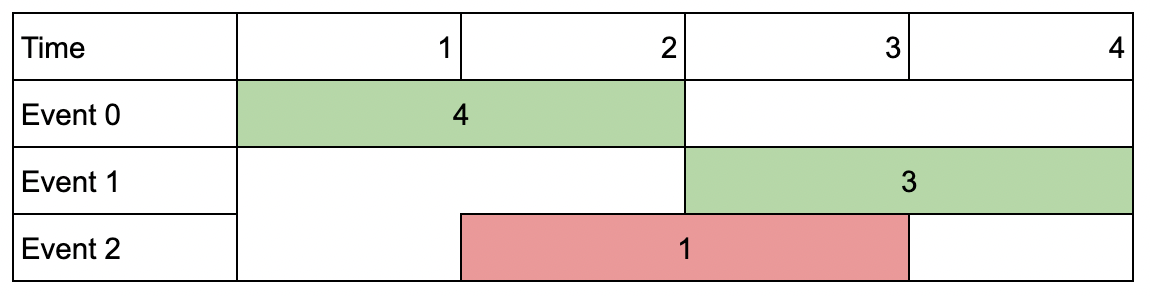
Input:
events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output:
 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.

Example 2:

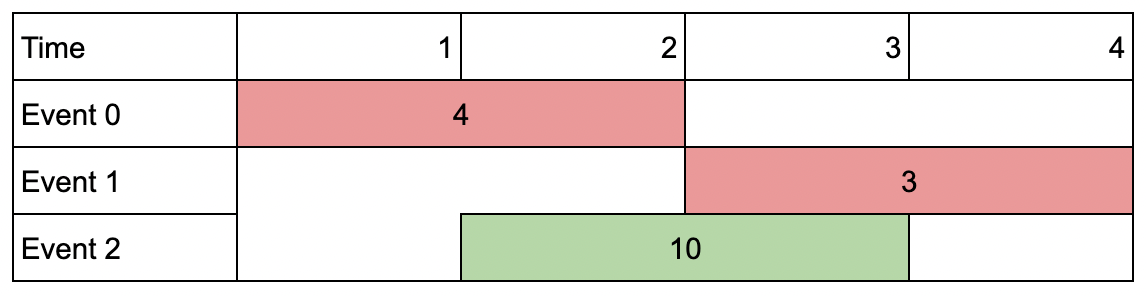
Input:
events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output:
 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.

Example 3:

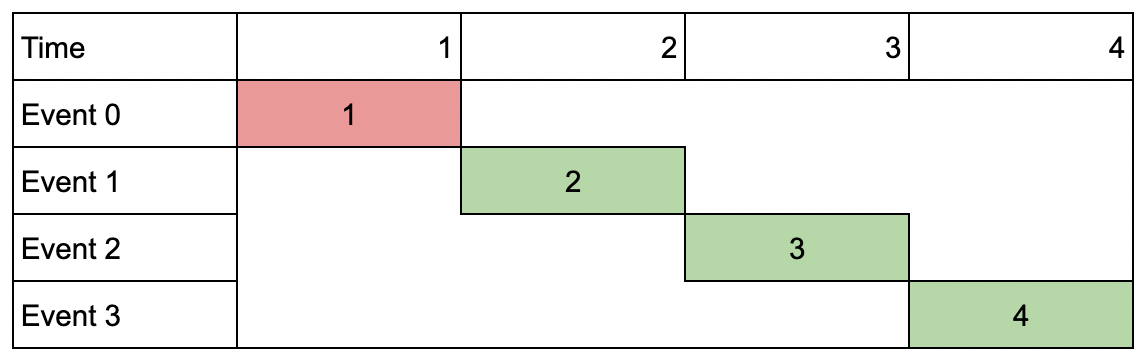
Input:
events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output:
 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.

Solution

or

Method 1 - DP with Memoization

Intuition

We want to select up to k non-overlapping events to maximize the total value. For each event, we can either attend it (if it doesn't overlap with the previous attended event) or skip it. We use dynamic programming with memoization to efficiently explore all possibilities.

Approach

1. Sort events by start time.
2. Use a recursive function with memoization to try attending or skipping each event.
3. If attending, move to the next event that starts after the current event ends, and decrease k.
4. If skipping, move to the next event and keep k unchanged.
5. The answer is the maximum value obtained.

Code

C++

class Solution {
public:
	int maxValue(vector<vector<int>>& events, int k) {
		sort(events.begin(), events.end());
		int n = events.size();
		vector<vector<int>> dp(n, vector<int>(k+1, -1));
		function<int(int, int, int)> dfs = [&](int idx, int k, int end) -> int {
			if (idx == n || k == 0) return 0;
			if (events[idx][0] <= end) return dfs(idx+1, k, end);
			if (dp[idx][k] != -1) return dp[idx][k];
			int attend = events[idx][2] + dfs(idx+1, k-1, events[idx][1]);
			int skip = dfs(idx+1, k, end);
			return dp[idx][k] = max(attend, skip);
		};
		return dfs(0, k, 0);
	}
};

Go

func maxValue(events [][]int, k int) int {
	sort.Slice(events, func(i, j int) bool { return events[i][0] < events[j][0] })
	n := len(events)
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, k+1)
		for j := range dp[i] {
			dp[i][j] = -1
		}
	}
	var dfs func(idx, k, end int) int
	dfs = func(idx, k, end int) int {
		if idx == n || k == 0 {
			return 0
		}
		if events[idx][0] <= end {
			return dfs(idx+1, k, end)
		}
		if dp[idx][k] != -1 {
			return dp[idx][k]
		}
		attend := events[idx][2] + dfs(idx+1, k-1, events[idx][1])
		skip := dfs(idx+1, k, end)
		dp[idx][k] = max(attend, skip)
		return dp[idx][k]
	}
	return dfs(0, k, 0)
}
func max(a, b int) int { if a > b { return a } else { return b } }

Java

class Solution {
	public int maxValue(int[][] events, int k) {
		Arrays.sort(events, (a, b) -> a[0] - b[0]);
		Integer[][] dp = new Integer[events.length][k + 1];
		return dfs(events, k, 0, dp, 0);
	}
	private int dfs(int[][] events, int k, int idx, Integer[][] dp, int end) {
		if (idx == events.length) return 0;
		if (k == 0) return 0;
		if (events[idx][0] <= end) return dfs(events, k, idx+1, dp, end);
		if (dp[idx][k] != null) return dp[idx][k];
		int attend = events[idx][2] + dfs(events, k-1, idx+1, dp, events[idx][1]);
		int skip = dfs(events, k, idx+1, dp, end);
		return dp[idx][k] = Math.max(attend, skip);
	}
}

Kotlin

class Solution {
	fun maxValue(events: Array<IntArray>, k: Int): Int {
		events.sortBy { it[0] }
		val n = events.size
		val dp = Array(n) { Array(k+1) { -1 } }
		fun dfs(idx: Int, k: Int, end: Int): Int {
			if (idx == n || k == 0) return 0
			if (events[idx][0] <= end) return dfs(idx+1, k, end)
			if (dp[idx][k] != -1) return dp[idx][k]
			val attend = events[idx][2] + dfs(idx+1, k-1, events[idx][1])
			val skip = dfs(idx+1, k, end)
			dp[idx][k] = maxOf(attend, skip)
			return dp[idx][k]
		}
		return dfs(0, k, 0)
	}
}

Python

class Solution:
	def maxValue(self, events: list[list[int]], k: int) -> int:
		events.sort()
		n = len(events)
		dp = [[-1]*(k+1) for _ in range(n)]
		def dfs(idx, k, end):
			if idx == n or k == 0:
				return 0
			if events[idx][0] <= end:
				return dfs(idx+1, k, end)
			if dp[idx][k] != -1:
				return dp[idx][k]
			attend = events[idx][2] + dfs(idx+1, k-1, events[idx][1])
			skip = dfs(idx+1, k, end)
			dp[idx][k] = max(attend, skip)
			return dp[idx][k]
		return dfs(0, k, 0)

Rust

impl Solution {
	pub fn max_value(events: Vec<Vec<i32>>, k: i32) -> i32 {
		let mut events = events;
		events.sort();
		let n = events.len();
		let mut dp = vec![vec![-1; (k+1) as usize]; n];
		fn dfs(idx: usize, k: i32, end: i32, events: &Vec<Vec<i32>>, dp: &mut Vec<Vec<i32>>) -> i32 {
			if idx == events.len() || k == 0 { return 0; }
			if events[idx][0] <= end { return dfs(idx+1, k, end, events, dp); }
			if dp[idx][k as usize] != -1 { return dp[idx][k as usize]; }
			let attend = events[idx][2] + dfs(idx+1, k-1, events[idx][1], events, dp);
			let skip = dfs(idx+1, k, end, events, dp);
			dp[idx][k as usize] = attend.max(skip);
			dp[idx][k as usize]
		}
		dfs(0, k, 0, &events, &mut dp)
	}
}

TypeScript

class Solution {
	maxValue(events: number[][], k: number): number {
		events.sort((a, b) => a[0] - b[0]);
		const n = events.length;
		const dp = Array.from({length: n}, () => Array(k+1).fill(-1));
		function dfs(idx: number, k: number, end: number): number {
			if (idx === n || k === 0) return 0;
			if (events[idx][0] <= end) return dfs(idx+1, k, end);
			if (dp[idx][k] !== -1) return dp[idx][k];
			const attend = events[idx][2] + dfs(idx+1, k-1, events[idx][1]);
			const skip = dfs(idx+1, k, end);
			dp[idx][k] = Math.max(attend, skip);
			return dp[idx][k];
		}
		return dfs(0, k, 0);
	}
}

Complexity

• ⏰ Time complexity: O(n*k)
  • There are n events and up to k choices for each event. The DP table has n*k states, and each state is computed once due to memoization. Sorting the events takes O(n log n), but the DP dominates.
  • For each DP state, we either skip or attend the event, so the recursion is bounded by the DP table size.
• 🧺 Space complexity: O(n*k)
  • The DP table stores results for each event and each possible remaining slot, resulting in n*k entries. The recursion stack is at most O(n) deep, but the DP table is the main space cost.