Maximum Number of Intersections on the Chart

Problem

There is a line chart consisting of n points connected by line segments. You are given a 1-indexed integer array y. The kth point has coordinates (k, y[k]). There are no horizontal lines; that is, no two consecutive points have the same y-coordinate.

We can draw an infinitely long horizontal line. Return themaximum number of points of intersection of the line with the chart.

Examples

Example 1:

**![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/3000-3099/3009.Maximum%20Number%20of%20Intersections%20on%20the%20Chart/images/20231208-020549.jpeg)**
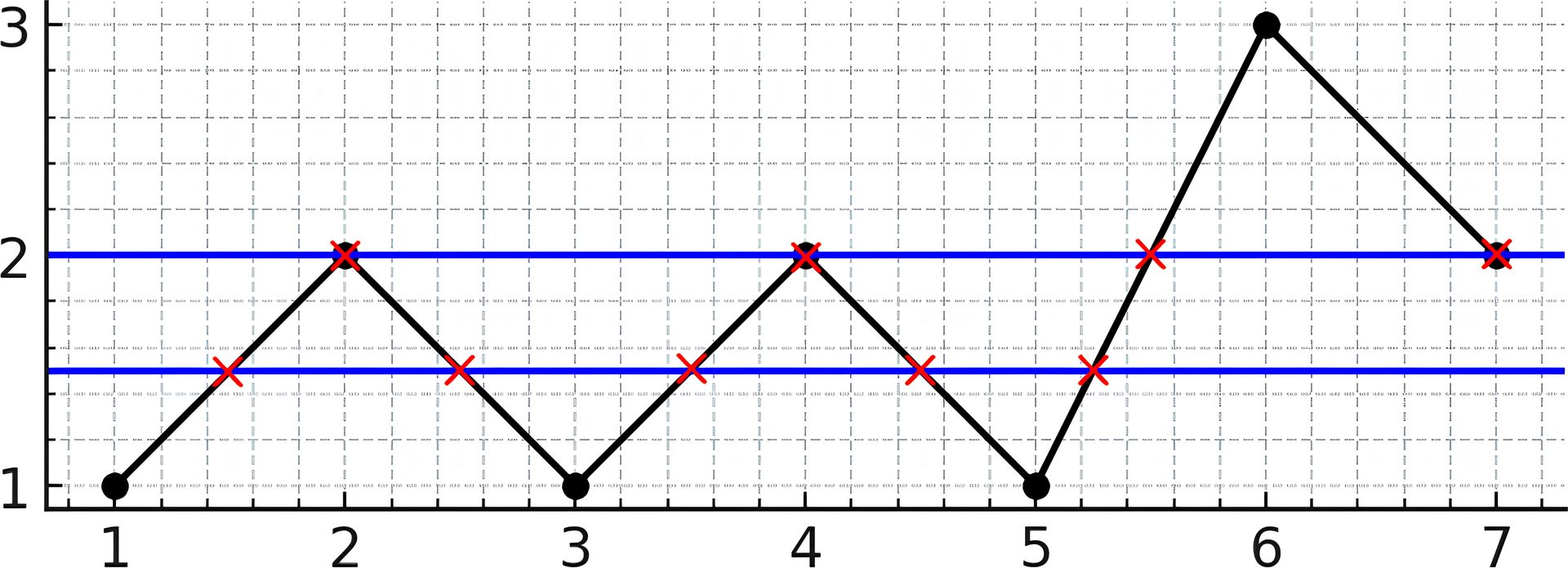Input: y = [1,2,1,2,1,3,2]
Output: 5
Explanation: As you can see in the image above, the line y = 1.5 has 5 intersections with the chart (in red crosses). You can also see the line y = 2 which intersects the chart in 4 points (in red crosses). It can be shown that there is no horizontal line intersecting the chart at more than 5 points. So the answer would be 5.

Example 2:

**![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/3000-3099/3009.Maximum%20Number%20of%20Intersections%20on%20the%20Chart/images/20231208-020557.jpeg)**
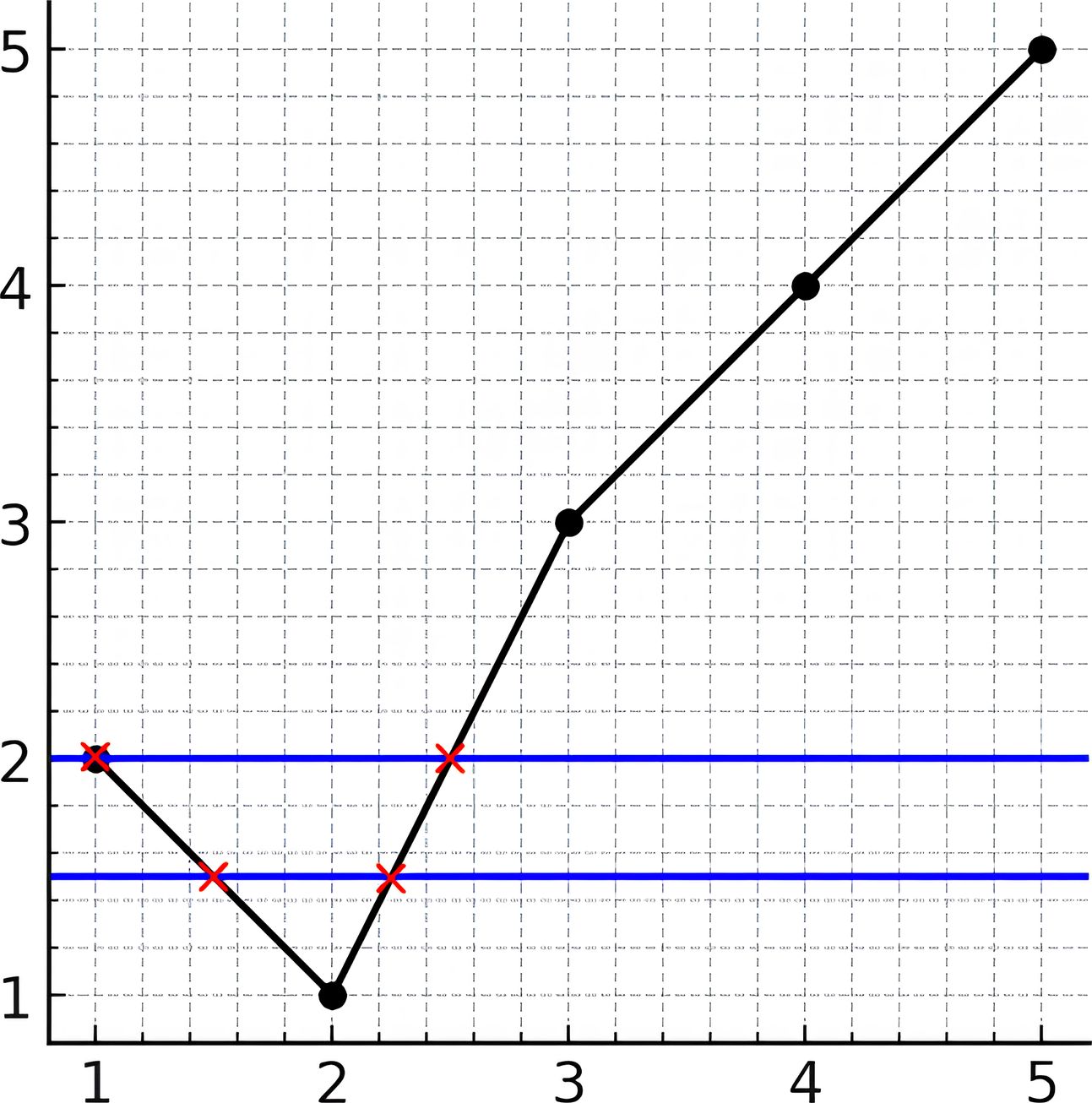Input: y = [2,1,3,4,5]
Output: 2
Explanation: As you can see in the image above, the line y = 1.5 has 2 intersections with the chart (in red crosses). You can also see the line y = 2 which intersects the chart in 2 points (in red crosses). It can be shown that there is no horizontal line intersecting the chart at more than 2 points. So the answer would be 2.

Constraints:

• 2 <= y.length <= 10^5
• 1 <= y[i] <= 10^9
• y[i] != y[i + 1] for i in range [1, n - 1]

Solution

Method 1 – Sweep Line (Interval Counting)

Intuition

Each segment between two consecutive points on the chart can be intersected by a horizontal line if the line's y-value is strictly between the two y-values. For each such segment, the interval (min(y[i], y[i+1]), max(y[i], y[i+1])) is a possible range for intersection. The problem reduces to finding the maximum number of overlapping intervals.

Approach

1. For each consecutive pair (y[i], y[i+1]), create an open interval (min(y[i], y[i+1]), max(y[i], y[i+1])).
2. For all intervals, collect all start and end points as events.
3. Sort the events, and sweep through them, incrementing a counter at each start and decrementing at each end.
4. Track the maximum value of the counter during the sweep.
5. Return the maximum overlap found.

Code

C++

class Solution {
public:
    int maxIntersectionCount(vector<int>& y) {
        vector<pair<int, int>> events;
        for (int i = 0; i + 1 < y.size(); ++i) {
            int a = min(y[i], y[i+1]), b = max(y[i], y[i+1]);
            events.emplace_back(a+1, 1);
            events.emplace_back(b, -1);
        }
        sort(events.begin(), events.end());
        int ans = 0, cnt = 0;
        for (auto& [pos, typ] : events) {
            cnt += typ;
            ans = max(ans, cnt);
        }
        return ans;
    }
};

Go

import "sort"
func maxIntersectionCount(y []int) int {
    events := [][2]int{}
    for i := 0; i+1 < len(y); i++ {
        a, b := y[i], y[i+1]
        if a > b { a, b = b, a }
        events = append(events, [2]int{a+1, 1}, [2]int{b, -1})
    }
    sort.Slice(events, func(i, j int) bool { return events[i][0] < events[j][0] })
    ans, cnt := 0, 0
    for _, e := range events {
        cnt += e[1]
        if cnt > ans { ans = cnt }
    }
    return ans
}

Java

import java.util.*;
class Solution {
    public int maxIntersectionCount(int[] y) {
        List<int[]> events = new ArrayList<>();
        for (int i = 0; i + 1 < y.length; i++) {
            int a = Math.min(y[i], y[i+1]), b = Math.max(y[i], y[i+1]);
            events.add(new int[]{a+1, 1});
            events.add(new int[]{b, -1});
        }
        events.sort(Comparator.comparingInt(a -> a[0]));
        int ans = 0, cnt = 0;
        for (int[] e : events) {
            cnt += e[1];
            ans = Math.max(ans, cnt);
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun maxIntersectionCount(y: IntArray): Int {
        val events = mutableListOf<Pair<Int, Int>>()
        for (i in 0 until y.size - 1) {
            val a = minOf(y[i], y[i+1])
            val b = maxOf(y[i], y[i+1])
            events.add(Pair(a+1, 1))
            events.add(Pair(b, -1))
        }
        events.sortBy { it.first }
        var ans = 0
        var cnt = 0
        for ((_, typ) in events) {
            cnt += typ
            ans = maxOf(ans, cnt)
        }
        return ans
    }
}

Python

class Solution:
    def maxIntersectionCount(self, y: list[int]) -> int:
        events = []
        for i in range(len(y)-1):
            a, b = min(y[i], y[i+1]), max(y[i], y[i+1])
            events.append((a+1, 1))
            events.append((b, -1))
        events.sort()
        ans = cnt = 0
        for _, typ in events:
            cnt += typ
            ans = max(ans, cnt)
        return ans

Rust

impl Solution {
    pub fn max_intersection_count(y: Vec<i32>) -> i32 {
        let mut events = vec![];
        for i in 0..y.len()-1 {
            let (a, b) = (y[i].min(y[i+1]), y[i].max(y[i+1]));
            events.push((a+1, 1));
            events.push((b, -1));
        }
        events.sort();
        let mut ans = 0;
        let mut cnt = 0;
        for (_, typ) in events {
            cnt += typ;
            ans = ans.max(cnt);
        }
        ans
    }
}

TypeScript

class Solution {
    maxIntersectionCount(y: number[]): number {
        const events: [number, number][] = [];
        for (let i = 0; i + 1 < y.length; i++) {
            const a = Math.min(y[i], y[i+1]), b = Math.max(y[i], y[i+1]);
            events.push([a+1, 1], [b, -1]);
        }
        events.sort((a, b) => a[0] - b[0]);
        let ans = 0, cnt = 0;
        for (const [_, typ] of events) {
            cnt += typ;
            ans = Math.max(ans, cnt);
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n log n), for sorting the events.
• 🧺 Space complexity: O(n), for storing the events.