Problem

You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.

To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.

However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.

Return the maximum number of points you can achieve.

abs(x) is defined as:

  • x for x >= 0.
  • -x for x < 0.

Examples

Example 1:

$$ points = \begin{bmatrix} 1 & 2 & \colorbox{lightblue} 3 \\ 1 & \colorbox{lightblue} 5 & 1 \\ \colorbox{lightblue} 3 & 1 & 1 \end{bmatrix} $$

1
2
3
4
5
6

Input: points =[[1,2,3],[1,5,1],[3,1,1]]
Output: 9
Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
Your final score is 11 - 2 = 9.

Example 2:

$$ grid = \begin{bmatrix} 1 & \colorbox{lightblue} 5 \\ 2 & \colorbox{lightblue} 3 \\ \colorbox{lightblue} 4 & 2 \end{bmatrix} $$

1
2
3
4
5
6

Input: points =[[1,5],[2,3],[4,2]]
Output: 11
Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.

Solution

Method 1 - Simple Dynamic Programming

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
    public long maxPoints(int[][] points) {
        int m = points.length;
        int n = points[0].length;
        long[][] dp = new long[m][n]; // null => not set

        // Set the first row of dp to the first row of points
        for (int i = 0; i < n; ++i) {
            dp[0][i] = points[0][i];
        }

        // Process the dp table
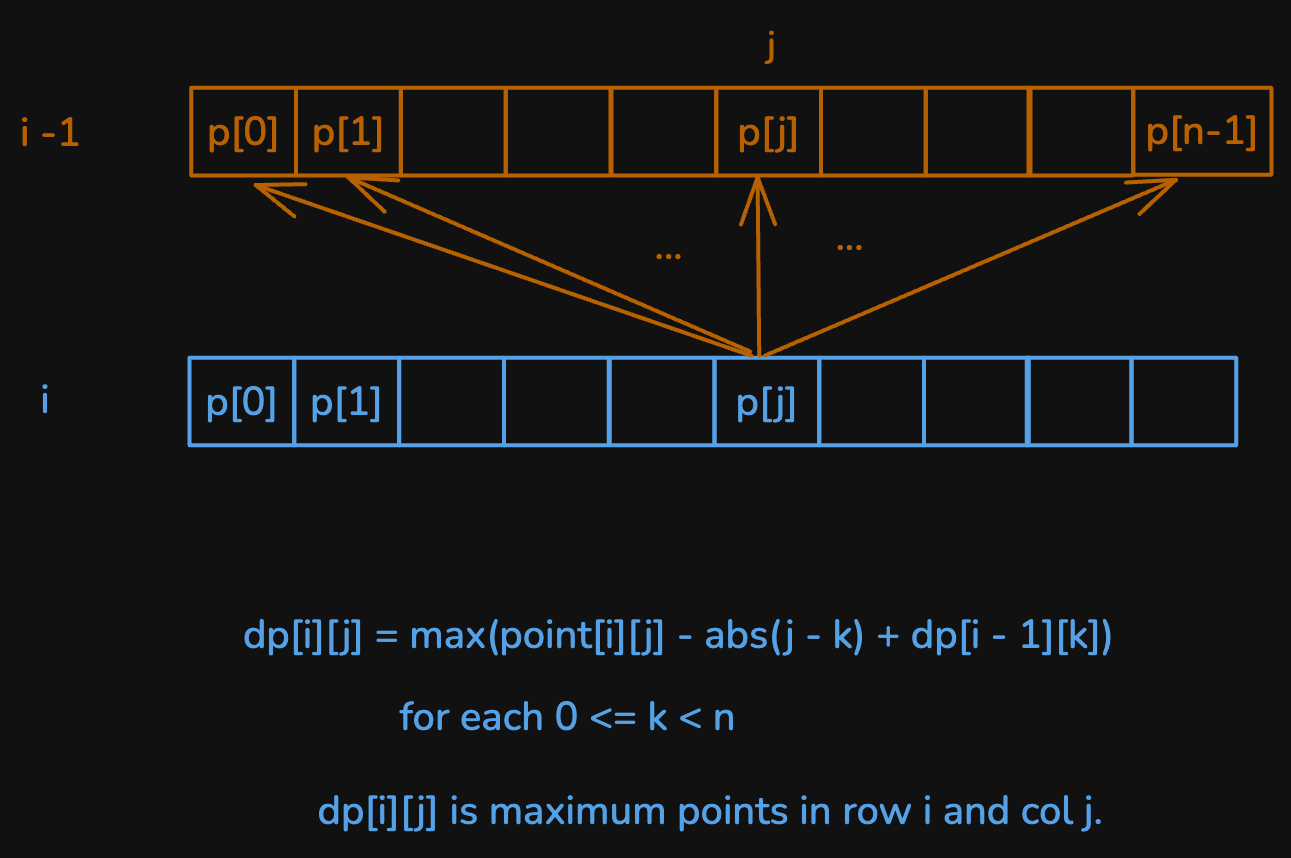
        for (int i = 1; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < n; ++k) {
                    dp[i][j] = Math.max(dp[i][j],
                        dp[i - 1][k] - Math.abs(k - j) + points[i][j]);
                }
            }
        }

        // Find the maximum value in the last row of dp
        long maxAns = -1;
        for (long v : dp[m - 1]) {
            maxAns = Math.max(maxAns, v);
        }

        return maxAns;
    }
}

Complexity

  • ⏰ Time complexity: O(m*n^2) where m is number of rows, and n is number of columns
    • This will result in TLE.
  • 🧺 Space complexity: O(m*n)

Method 2 - Optimal DP with left and right max

Previous solution was good, but we don’t want to literally compare every index in previous row to find the max points in the current row.

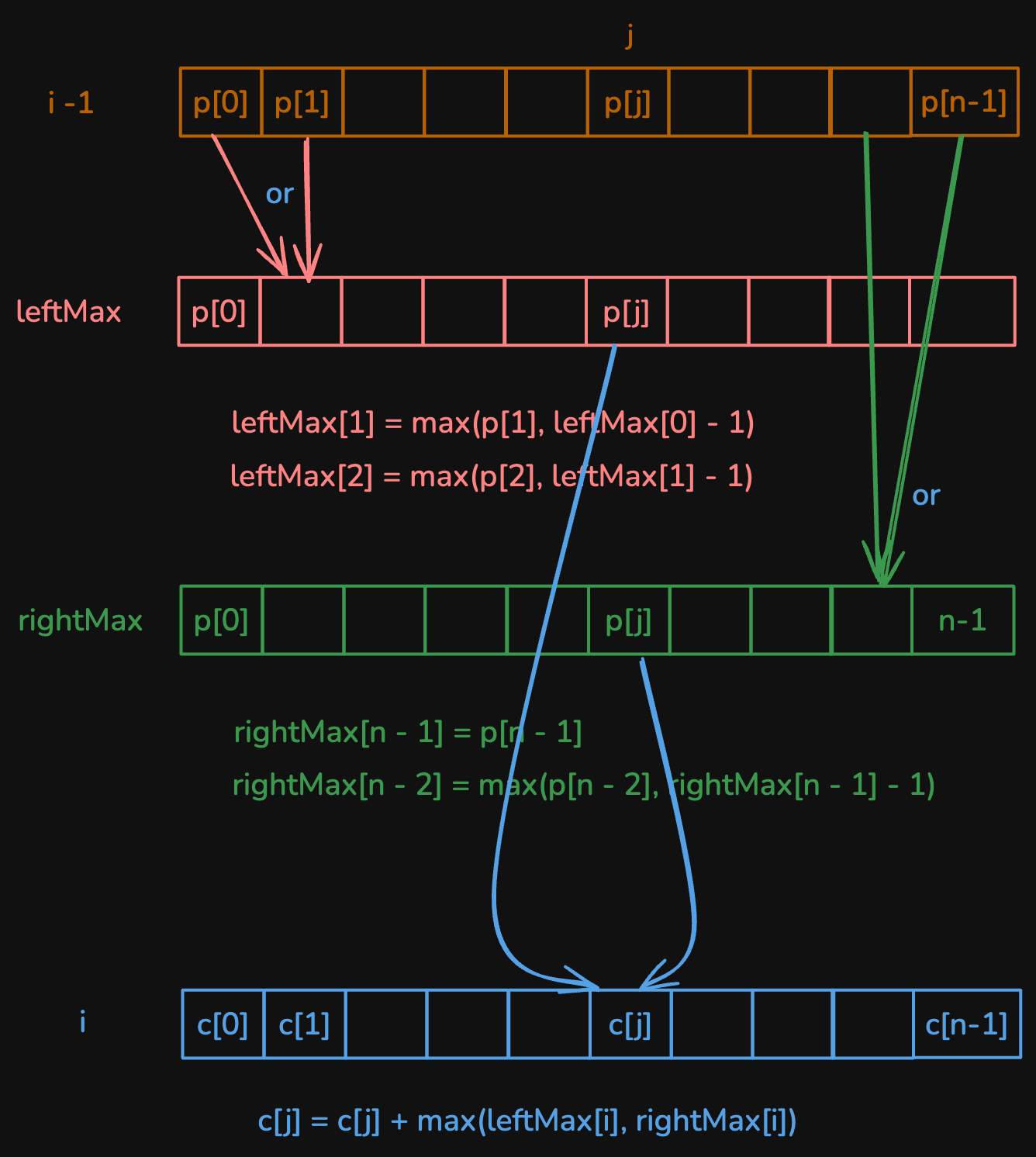
But if we look closely, the current row’s points for a certain index j, can also come from its left or right (inclusive). So, we can build two arrays - leftMax and rightMax, and focus on the maximum value coming from its left or right.

So, we can take leftMax[0] = prev[0], where prev is previous row.

Now, leftMax[1] = max(prev[1], leftMax[0] - 1) Similarly, leftMax[2] = max(prev[2], leftMax[1] - 1)

Now, question is why it is sufficient to compareleftMax[1] - 1 and not leftMax[0] - 2 for filling in leftMax[2]? And the reason is we already chose the optimal answer in leftMax[1].

Similarly, we build rightMax from the right.

1
2

rightMax[n - 1] = prev[n - 1]
rightMax[n - 2] = max(prev[n - 2], rightMax[n - 1] - 1)

.

Approach

  1. Initialization: Use a DP array to keep track of the maximum points that can be achieved for each cell in the current row.
  2. Transition: For each cell in the current row, we need to consider all cells from the previous row. The points gained from the current cell should include the points from the previous cell minus the distance penalty.
  3. Optimization: To optimize the calculation, we can maintain two forward and backward sweeps to precompute the best points that can be achieved from any cell.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

public class Solution {
    public long maxPoints(int[][] points) {
        int m = points.length;
        int n = points[0].length;
        long[] dp = new long[n];

        // Initially copy the first row into dp
        for (int j = 0; j < n; j++) {
            dp[j] = points[0][j];
        }

        // Process each row starting from the second row
        for (int i = 1; i < m; i++) {
            long[] leftMax = new long[n];
            long[] rightMax = new long[n];

            // Calculate the maximum values considering left to right
            leftMax[0] = dp[0];
            for (int j = 1; j < n; j++) {
                leftMax[j] = Math.max(leftMax[j - 1] - 1, dp[j]);
            }

            // Calculate the maximum values considering right to left
            rightMax[n - 1] = dp[n - 1];
            for (int j = n - 2; j >= 0; j--) {
                rightMax[j] = Math.max(rightMax[j + 1] - 1, dp[j]);
            }

            // Update dp array with the maximum achievable points for the
            // current row
            for (int j = 0; j < n; j++) {
                dp[j] = points[i][j] + Math.max(leftMax[j], rightMax[j]);
            }
        }

        // The result is the maximum value in the dp array
        long maxPoints = 0;
        for (int j = 0; j < n; j++) {
            maxPoints = Math.max(maxPoints, dp[j]);
        }

        return maxPoints;
    }
}

Complexity

  • Time: O(m*n)
  • Space: O(m)