Problem

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the ith node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [uj, vj, timej] indicates that there is an undirected edge between the nodes uj and vj, and it takes timej seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node’s value is added at most once to the sum).

Return themaximum quality of a valid path.

Note: There are at most four edges connected to each node.

Examples

Example 1

1
2
3
4
5
6
7
8


![](https://assets.leetcode.com/uploads/2021/10/19/ex1drawio.png)

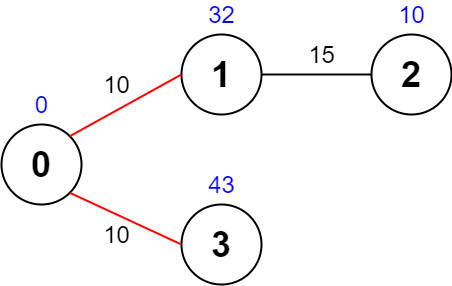
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2

1
2
3
4
5
6
7
8


![](https://assets.leetcode.com/uploads/2021/10/19/ex2drawio.png)

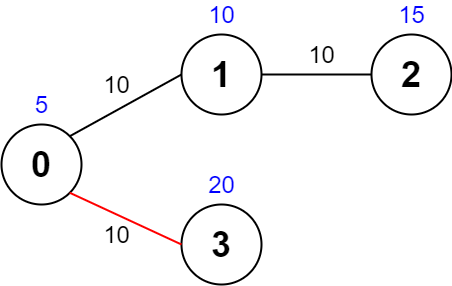
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3

1
2
3
4
5
6
7
8


![](https://assets.leetcode.com/uploads/2021/10/19/ex31drawio.png)

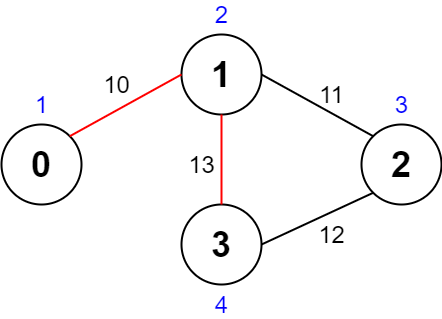
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Constraints

  • n == values.length
  • 1 <= n <= 1000
  • 0 <= values[i] <= 10^8
  • 0 <= edges.length <= 2000
  • edges[j].length == 3
  • 0 <= uj < vj <= n - 1
  • 10 <= timej, maxTime <= 100
  • All the pairs [uj, vj] are unique.
  • There are at most four edges connected to each node.
  • The graph may not be connected.

Solution

Method 1 – Backtracking with State Tracking

Intuition

Since the graph is small (at most 100 nodes, each with at most 4 edges), we can use backtracking (DFS) to explore all valid paths starting and ending at node 0 within the time limit. We keep track of the set of unique nodes visited and the current path quality, updating the answer whenever we return to node 0.

Approach

  1. Build the adjacency list for the graph from the edges.
  2. Use DFS to explore all paths starting from node 0, tracking:
    • The current node, time used, current path quality, and a visited count for each node.
  3. When visiting a node for the first time, add its value to the current quality.
  4. If we return to node 0 within the time limit, update the answer with the current quality.
  5. For each neighbor, if the next time does not exceed maxTime, recurse.
  6. Backtrack the visited count after recursion.
  7. Return the maximum quality found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int maxQuality = 0;
    void dfs(int u, int time, int quality, vector<int>& values, vector<vector<pair<int,int>>>& g, vector<int>& vis, int maxTime) {
        if (vis[u] == 0) quality += values[u];
        vis[u]++;
        if (u == 0) maxQuality = max(maxQuality, quality);
        for (auto& [v, t] : g[u]) {
            if (time + t <= maxTime) {
                dfs(v, time + t, quality, values, g, vis, maxTime);
            }
        }
        vis[u]--;
    }
    int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {
        int n = values.size();
        vector<vector<pair<int,int>>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back({e[1], e[2]});
            g[e[1]].push_back({e[0], e[2]});
        }
        vector<int> vis(n, 0);
        dfs(0, 0, 0, values, g, vis, maxTime);
        return maxQuality;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func maximalPathQuality(values []int, edges [][]int, maxTime int) int {
    n := len(values)
    g := make([][][2]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
        g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
    }
    ans := 0
    vis := make([]int, n)
    var dfs func(u, time, quality int)
    dfs = func(u, time, quality int) {
        if vis[u] == 0 {
            quality += values[u]
        }
        vis[u]++
        if u == 0 {
            if quality > ans {
                ans = quality
            }
        }
        for _, e := range g[u] {
            v, t := e[0], e[1]
            if time + t <= maxTime {
                dfs(v, time + t, quality)
            }
        }
        vis[u]--
    }
    dfs(0, 0, 0)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    int ans = 0;
    public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {
        int n = values.length;
        List<int[]>[] g = new List[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        int[] vis = new int[n];
        dfs(0, 0, 0, values, g, vis, maxTime);
        return ans;
    }
    void dfs(int u, int time, int quality, int[] values, List<int[]>[] g, int[] vis, int maxTime) {
        if (vis[u] == 0) quality += values[u];
        vis[u]++;
        if (u == 0) ans = Math.max(ans, quality);
        for (int[] e : g[u]) {
            int v = e[0], t = e[1];
            if (time + t <= maxTime) {
                dfs(v, time + t, quality, values, g, vis, maxTime);
            }
        }
        vis[u]--;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    var ans = 0
    fun maximalPathQuality(values: IntArray, edges: Array<IntArray>, maxTime: Int): Int {
        val n = values.size
        val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
        for (e in edges) {
            g[e[0]].add(e[1] to e[2])
            g[e[1]].add(e[0] to e[2])
        }
        val vis = IntArray(n)
        fun dfs(u: Int, time: Int, quality: Int) {
            var q = quality
            if (vis[u] == 0) q += values[u]
            vis[u]++
            if (u == 0) ans = maxOf(ans, q)
            for ((v, t) in g[u]) {
                if (time + t <= maxTime) dfs(v, time + t, q)
            }
            vis[u]--
        }
        dfs(0, 0, 0)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution:
    def maximalPathQuality(self, values: list[int], edges: list[list[int]], maxTime: int) -> int:
        from collections import defaultdict
        g = defaultdict(list)
        for u, v, t in edges:
            g[u].append((v, t))
            g[v].append((u, t))
        n = len(values)
        ans = 0
        vis = [0] * n
        def dfs(u: int, time: int, quality: int):
            nonlocal ans
            if vis[u] == 0:
                quality += values[u]
            vis[u] += 1
            if u == 0:
                ans = max(ans, quality)
            for v, t in g[u]:
                if time + t <= maxTime:
                    dfs(v, time + t, quality)
            vis[u] -= 1
        dfs(0, 0, 0)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

impl Solution {
    pub fn maximal_path_quality(values: Vec<i32>, edges: Vec<Vec<i32>>, max_time: i32) -> i32 {
        use std::collections::HashMap;
        let n = values.len();
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push((e[1] as usize, e[2]));
            g[e[1] as usize].push((e[0] as usize, e[2]));
        }
        let mut vis = vec![0; n];
        let mut ans = 0;
        fn dfs(u: usize, time: i32, quality: i32, values: &Vec<i32>, g: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<i32>, max_time: i32, ans: &mut i32) {
            let mut q = quality;
            if vis[u] == 0 {
                q += values[u];
            }
            vis[u] += 1;
            if u == 0 {
                *ans = (*ans).max(q);
            }
            for &(v, t) in &g[u] {
                if time + t <= max_time {
                    dfs(v, time + t, q, values, g, vis, max_time, ans);
                }
            }
            vis[u] -= 1;
        }
        dfs(0, 0, 0, &values, &g, &mut vis, max_time, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
    maximalPathQuality(values: number[], edges: number[][], maxTime: number): number {
        const n = values.length;
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [u, v, t] of edges) {
            g[u].push([v, t]);
            g[v].push([u, t]);
        }
        let ans = 0;
        const vis = new Array(n).fill(0);
        function dfs(u: number, time: number, quality: number) {
            if (vis[u] === 0) quality += values[u];
            vis[u]++;
            if (u === 0) ans = Math.max(ans, quality);
            for (const [v, t] of g[u]) {
                if (time + t <= maxTime) dfs(v, time + t, quality);
            }
            vis[u]--;
        }
        dfs(0, 0, 0);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(4^n) in the worst case, but practical due to small graph size and pruning by maxTime.
  • 🧺 Space complexity: O(n) for the recursion stack and visited array.