Maximum Product of the Length of Two Palindromic Subsequences Problem

Problem

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

Example 1:

Input:
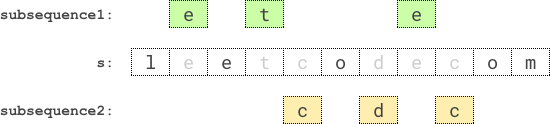
s = "leetcodecom"
Output:
 9
**Explanation**: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input:
s = "bb"
Output:
 1
**Explanation**: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input:
s = "accbcaxxcxx"
Output:
 25
**Explanation**: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

Examples

Solution

Method 1 – Bitmask + Palindrome Check

Intuition

Enumerate all possible ways to split the string into two disjoint subsequences using bitmasks, and for each, check if both are palindromic and maximize the product of their lengths.

Approach

1. For each bitmask from 1 to (1 << n) - 2, assign characters to the first subsequence if the bit is set, and to the second if not.
2. For each split, check if both subsequences are palindromic.
3. Track the maximum product of their lengths.

Code

C++

class Solution {
public:
    int maxProduct(string s) {
        int n = s.size(), res = 0;
        auto isPal = [](const string& t) {
            int l = 0, r = t.size()-1;
            while (l < r) if (t[l++] != t[r--]) return false;
            return true;
        };
        for (int mask = 1; mask < (1<<n)-1; ++mask) {
            string a, b;
            for (int i = 0; i < n; ++i) {
                if (mask & (1<<i)) a += s[i];
                else b += s[i];
            }
            if (isPal(a) && isPal(b)) res = max(res, int(a.size()*b.size()));
        }
        return res;
    }
};

Go

func maxProduct(s string) int {
    n := len(s)
    isPal := func(t string) bool {
        l, r := 0, len(t)-1
        for l < r {
            if t[l] != t[r] { return false }
            l++; r--
        }
        return true
    }
    res := 0
    for mask := 1; mask < (1<<n)-1; mask++ {
        a, b := "", ""
        for i := 0; i < n; i++ {
            if mask&(1<<i) > 0 { a += string(s[i]) } else { b += string(s[i]) }
        }
        if isPal(a) && isPal(b) {
            prod := len(a)*len(b)
            if prod > res { res = prod }
        }
    }
    return res
}

Java

class Solution {
    public int maxProduct(String s) {
        int n = s.length(), res = 0;
        for (int mask = 1; mask < (1<<n)-1; ++mask) {
            StringBuilder a = new StringBuilder(), b = new StringBuilder();
            for (int i = 0; i < n; ++i) {
                if ((mask & (1<<i)) > 0) a.append(s.charAt(i));
                else b.append(s.charAt(i));
            }
            if (isPal(a) && isPal(b)) res = Math.max(res, a.length()*b.length());
        }
        return res;
    }
    private boolean isPal(CharSequence t) {
        int l = 0, r = t.length()-1;
        while (l < r) if (t.charAt(l++) != t.charAt(r--)) return false;
        return true;
    }
}

Kotlin

class Solution {
    fun maxProduct(s: String): Int {
        val n = s.length
        fun isPal(t: String): Boolean {
            var l = 0; var r = t.length-1
            while (l < r) if (t[l++] != t[r--]) return false
            return true
        }
        var res = 0
        for (mask in 1 until (1 shl n)-1) {
            val a = StringBuilder(); val b = StringBuilder()
            for (i in 0 until n) {
                if ((mask shr i) and 1 == 1) a.append(s[i]) else b.append(s[i])
            }
            if (isPal(a.toString()) && isPal(b.toString()))
                res = maxOf(res, a.length*b.length)
        }
        return res
    }
}

Python

class Solution:
    def maxProduct(self, s: str) -> int:
        def is_pal(t): return t == t[::-1]
        n, res = len(s), 0
        for mask in range(1, (1<<n)-1):
            a, b = [], []
            for i in range(n):
                if mask & (1<<i): a.append(s[i])
                else: b.append(s[i])
            a, b = ''.join(a), ''.join(b)
            if is_pal(a) and is_pal(b): res = max(res, len(a)*len(b))
        return res

Rust

impl Solution {
    pub fn max_product(s: String) -> i32 {
        fn is_pal(t: &str) -> bool {
            t.chars().eq(t.chars().rev())
        }
        let n = s.len();
        let s_bytes = s.as_bytes();
        let mut res = 0;
        for mask in 1..(1<<n)-1 {
            let mut a = Vec::new();
            let mut b = Vec::new();
            for i in 0..n {
                if (mask & (1<<i)) > 0 { a.push(s_bytes[i]); }
                else { b.push(s_bytes[i]); }
            }
            let a_str = String::from_utf8(a.clone()).unwrap();
            let b_str = String::from_utf8(b.clone()).unwrap();
            if is_pal(&a_str) && is_pal(&b_str) {
                let prod = a_str.len() * b_str.len();
                if prod > res { res = prod as i32; }
            }
        }
        res
    }
}

TypeScript

class Solution {
    maxProduct(s: string): number {
        const n = s.length;
        function isPal(t: string): boolean {
            return t === t.split('').reverse().join('');
        }
        let res = 0;
        for (let mask = 1; mask < (1<<n)-1; ++mask) {
            let a = '', b = '';
            for (let i = 0; i < n; ++i) {
                if (mask & (1<<i)) a += s[i];
                else b += s[i];
            }
            if (isPal(a) && isPal(b)) res = Math.max(res, a.length * b.length);
        }
        return res;
    }
}

Complexity

• ⏰ Time complexity: O(2^n * n)
  • We enumerate all possible splits (2^n), and for each, check if both subsequences are palindromic (O(n)).
• 🧺 Space complexity: O(n)
  • We use space for the two subsequences and temporary variables.