Problem

You have n computers. You are given the integer n and a 0-indexed integer array batteries where the ith battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.

Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.

Note that the batteries cannot be recharged.

Return _themaximum number of minutes you can run all the _n computers simultaneously.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


![](https://assets.leetcode.com/uploads/2022/01/06/example1-fit.png)

Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation: 
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


![](https://assets.leetcode.com/uploads/2022/01/06/example2.png)

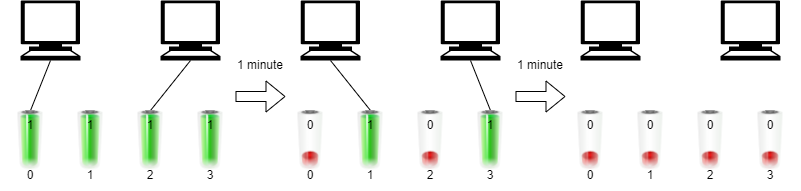
Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation: 
Initially, insert battery 0 into the first computer and battery 2 into the second computer. 
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer. 
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.

Constraints

  • 1 <= n <= batteries.length <= 10^5
  • 1 <= batteries[i] <= 10^9

Solution

Method 1 – Binary Search + Greedy

Intuition

We want to maximize the time all n computers can run simultaneously using the given batteries. The key is that batteries can be swapped at any time, so the total available energy can be distributed optimally. The answer is the largest integer T such that the sum of the min(battery, T) for all batteries is at least n * T.

Approach

  1. Compute the total sum of all battery capacities.
  2. Use binary search between 1 and total // n (the theoretical upper bound for running time).
  3. For each candidate time T, check if the sum of min(battery, T) for all batteries is at least n * T.
  4. Return the largest valid T.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    long long maxRunTime(int n, vector<int>& batteries) {
        long long left = 1, right = accumulate(batteries.begin(), batteries.end(), 0LL) / n, ans = 0;
        while (left <= right) {
            long long mid = left + (right - left) / 2, total = 0;
            for (int b : batteries) total += min((long long)b, mid);
            if (total >= n * mid) {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

func maxRunTime(n int, batteries []int) int64 {
    sum := int64(0)
    for _, b := range batteries {
        sum += int64(b)
    }
    left, right, ans := int64(1), sum/int64(n), int64(0)
    for left <= right {
        mid := left + (right-left)/2
        total := int64(0)
        for _, b := range batteries {
            if int64(b) < mid {
                total += int64(b)
            } else {
                total += mid
            }
        }
        if total >= int64(n)*mid {
            ans = mid
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
    public long maxRunTime(int n, int[] batteries) {
        long sum = 0;
        for (int b : batteries) sum += b;
        long left = 1, right = sum / n, ans = 0;
        while (left <= right) {
            long mid = left + (right - left) / 2, total = 0;
            for (int b : batteries) total += Math.min(b, mid);
            if (total >= n * mid) {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    fun maxRunTime(n: Int, batteries: IntArray): Long {
        var sum = batteries.map { it.toLong() }.sum()
        var left = 1L
        var right = sum / n
        var ans = 0L
        while (left <= right) {
            val mid = left + (right - left) / 2
            var total = 0L
            for (b in batteries) total += minOf(b.toLong(), mid)
            if (total >= n * mid) {
                ans = mid
                left = mid + 1
            } else {
                right = mid - 1
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def maxRunTime(self, n: int, batteries: list[int]) -> int:
        total = sum(batteries)
        left, right, ans = 1, total // n, 0
        while left <= right:
            mid = (left + right) // 2
            s = sum(min(b, mid) for b in batteries)
            if s >= n * mid:
                ans = mid
                left = mid + 1
            else:
                right = mid - 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

impl Solution {
    pub fn max_run_time(n: i32, batteries: Vec<i32>) -> i64 {
        let sum: i64 = batteries.iter().map(|&b| b as i64).sum();
        let (mut left, mut right, mut ans) = (1, sum / n as i64, 0);
        while left <= right {
            let mid = left + (right - left) / 2;
            let total: i64 = batteries.iter().map(|&b| std::cmp::min(b as i64, mid)).sum();
            if total >= n as i64 * mid {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    maxRunTime(n: number, batteries: number[]): number {
        let sum = batteries.reduce((a, b) => a + b, 0);
        let left = 1, right = Math.floor(sum / n), ans = 0;
        while (left <= right) {
            let mid = Math.floor((left + right) / 2);
            let total = batteries.reduce((acc, b) => acc + Math.min(b, mid), 0);
            if (total >= n * mid) {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(m log S), where m is the number of batteries and S is the sum of all battery capacities (since binary search is over [1, S/n]).
  • 🧺 Space complexity: O(1), only a few variables are used.