Maximum Score of a Node Sequence

Problem

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

A node sequence is valid if it meets the following conditions:

There is an edge connecting every pair of adjacent nodes in the sequence.
No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return _themaximum score of a valid node sequence with a length of _4 . If no such sequence exists, return __-1.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10



![](https://assets.leetcode.com/uploads/2022/04/15/ex1new3.png)

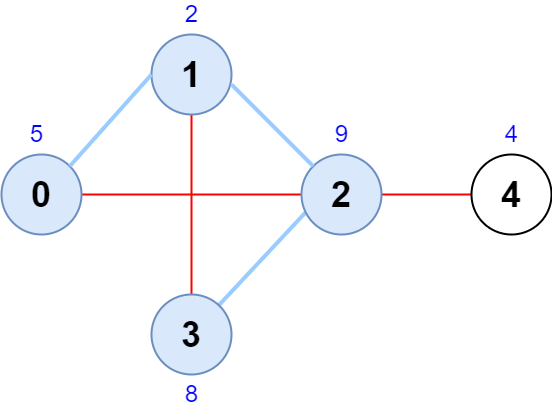
Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2

1
2
3
4
5
6
7



![](https://assets.leetcode.com/uploads/2022/03/17/ex2.png)

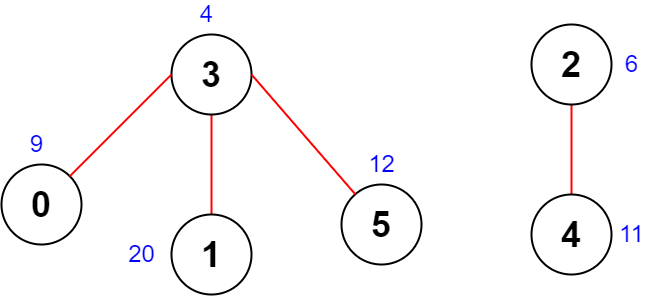
Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

Constraints

n == scores.length
4 <= n <= 5 * 10^4
1 <= scores[i] <= 10^8
0 <= edges.length <= 5 * 10^4
edges[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
There are no duplicate edges.

Solution

Method 1 – Greedy Enumeration with Top Neighbors

Intuition

To maximize the score of a valid node sequence of length 4, we want to pick two adjacent nodes (b, c) and extend them to the left and right with their best neighbors (a, d) that are not already in the sequence. For each edge (b, c), we try all possible top 3 neighbors for b (excluding c) and top 3 neighbors for c (excluding b), and compute the score if all nodes are unique.

Approach

For each node, keep a list of its top 3 neighbors with the highest scores (for efficiency).
For each edge (b, c), try all combinations of a in b’s top neighbors (excluding c) and d in c’s top neighbors (excluding b).
For each combination, if all nodes are unique, compute the score and update the answer.
Return the maximum score found, or -1 if no valid sequence exists.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


class Solution {
public:
    int maximumScore(vector<int>& scores, vector<vector<int>>& edges) {
        int n = scores.size(), ans = -1;
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        vector<vector<int>> top3(n);
        for (int i = 0; i < n; ++i) {
            sort(g[i].begin(), g[i].end(), [&](int a, int b) {
                return scores[a] > scores[b];
            });
            for (int j = 0; j < min(3, (int)g[i].size()); ++j)
                top3[i].push_back(g[i][j]);
        }
        for (auto& e : edges) {
            int b = e[0], c = e[1];
            for (int a : top3[b]) {
                if (a == c) continue;
                for (int d : top3[c]) {
                    if (d == b || d == a) continue;
                    ans = max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
            for (int a : top3[c]) {
                if (a == b) continue;
                for (int d : top3[b]) {
                    if (d == c || d == a) continue;
                    ans = max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


func maximumScore(scores []int, edges [][]int) int {
    n := len(scores)
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    top3 := make([][]int, n)
    for i := 0; i < n; i++ {
        sort.Slice(g[i], func(a, b int) bool { return scores[g[i][a]] > scores[g[i][b]] })
        for j := 0; j < 3 && j < len(g[i]); j++ {
            top3[i] = append(top3[i], g[i][j])
        }
    }
    ans := -1
    for _, e := range edges {
        b, c := e[0], e[1]
        for _, a := range top3[b] {
            if a == c { continue }
            for _, d := range top3[c] {
                if d == b || d == a { continue }
                sum := scores[a] + scores[b] + scores[c] + scores[d]
                if sum > ans { ans = sum }
            }
        }
        for _, a := range top3[c] {
            if a == b { continue }
            for _, d := range top3[b] {
                if d == c || d == a { continue }
                sum := scores[a] + scores[b] + scores[c] + scores[d]
                if sum > ans { ans = sum }
            }
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


class Solution {
    public int maximumScore(int[] scores, int[][] edges) {
        int n = scores.length, ans = -1;
        List<Integer>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        List<Integer>[] top3 = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            g[i].sort((a, b) -> scores[b] - scores[a]);
            top3[i] = new ArrayList<>();
            for (int j = 0; j < Math.min(3, g[i].size()); j++)
                top3[i].add(g[i].get(j));
        }
        for (int[] e : edges) {
            int b = e[0], c = e[1];
            for (int a : top3[b]) {
                if (a == c) continue;
                for (int d : top3[c]) {
                    if (d == b || d == a) continue;
                    ans = Math.max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
            for (int a : top3[c]) {
                if (a == b) continue;
                for (int d : top3[b]) {
                    if (d == c || d == a) continue;
                    ans = Math.max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


class Solution {
    fun maximumScore(scores: IntArray, edges: Array<IntArray>): Int {
        val n = scores.size
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val top3 = Array(n) { mutableListOf<Int>() }
        for (i in 0 until n) {
            g[i].sortByDescending { scores[it] }
            for (j in 0 until minOf(3, g[i].size))
                top3[i].add(g[i][j])
        }
        var ans = -1
        for (e in edges) {
            val (b, c) = e
            for (a in top3[b]) {
                if (a == c) continue
                for (d in top3[c]) {
                    if (d == b || d == a) continue
                    ans = maxOf(ans, scores[a] + scores[b] + scores[c] + scores[d])
                }
            }
            for (a in top3[c]) {
                if (a == b) continue
                for (d in top3[b]) {
                    if (d == c || d == a) continue
                    ans = maxOf(ans, scores[a] + scores[b] + scores[c] + scores[d])
                }
            }
        }
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution:
    def maximumScore(self, scores: list[int], edges: list[list[int]]) -> int:
        n = len(scores)
        g = [[] for _ in range(n)]
        for u, v in edges:
            g[u].append(v)
            g[v].append(u)
        top3 = [sorted(g[i], key=lambda x: -scores[x])[:3] for i in range(n)]
        ans = -1
        for b, c in edges:
            for a in top3[b]:
                if a == c: continue
                for d in top3[c]:
                    if d == b or d == a: continue
                    ans = max(ans, scores[a] + scores[b] + scores[c] + scores[d])
            for a in top3[c]:
                if a == b: continue
                for d in top3[b]:
                    if d == c or d == a: continue
                    ans = max(ans, scores[a] + scores[b] + scores[c] + scores[d])
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


impl Solution {
    pub fn maximum_score(scores: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
        let n = scores.len();
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let mut top3 = vec![vec![]; n];
        for i in 0..n {
            g[i].sort_by_key(|&x| -scores[x]);
            for j in 0..g[i].len().min(3) {
                top3[i].push(g[i][j]);
            }
        }
        let mut ans = -1;
        for e in &edges {
            let (b, c) = (e[0] as usize, e[1] as usize);
            for &a in &top3[b] {
                if a == c { continue; }
                for &d in &top3[c] {
                    if d == b || d == a { continue; }
                    ans = ans.max(scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
            for &a in &top3[c] {
                if a == b { continue; }
                for &d in &top3[b] {
                    if d == c || d == a { continue; }
                    ans = ans.max(scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
        }
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


class Solution {
    maximumScore(scores: number[], edges: number[][]): number {
        const n = scores.length;
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [u, v] of edges) {
            g[u].push(v);
            g[v].push(u);
        }
        const top3 = g.map(neighs => [...neighs].sort((a, b) => scores[b] - scores[a]).slice(0, 3));
        let ans = -1;
        for (const [b, c] of edges) {
            for (const a of top3[b]) {
                if (a === c) continue;
                for (const d of top3[c]) {
                    if (d === b || d === a) continue;
                    ans = Math.max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
            for (const a of top3[c]) {
                if (a === b) continue;
                for (const d of top3[b]) {
                    if (d === c || d === a) continue;
                    ans = Math.max(ans, scores[a] + scores[b] + scores[c] + scores[d]);
                }
            }
        }
        return ans;
    }
}

Complexity

⏰ Time complexity: O(m * 9), where m is the number of edges. For each edge, we try up to 9 combinations (3 neighbors for each side).
🧺 Space complexity: O(n + m), for the adjacency list and top neighbors.

Problem#

Examples#

Example 1#

Example 2#

Constraints#

Solution#

Method 1 – Greedy Enumeration with Top Neighbors#

Intuition#

Approach#

Code#

Complexity#