Problem

Given a list of words, list of  single letters (might be repeating) and score of every character.

Return the maximum score of any valid set of words formed by using the given letters (words[i] cannot be used two or more times).

It is not necessary to use all characters in letters and each letter can only be used once. Score of letters 'a', 'b', 'c', … ,'z' is given by score[0], score[1], … , score[25] respectively.

Examples

Example 1:

1
2
3
4
5
6

Input: words = ["dog","cat","dad","good"], letters = ["a","a","c","d","d","d","g","o","o"], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
Output: 23
Explanation:
Score  a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad" (5+1+5) and "good" (3+2+2+5) with a score of 23.
Words "dad" and "dog" only get a score of 21.

Example 2:

1
2
3
4
5
6

Input: words = ["xxxz","ax","bx","cx"], letters = ["z","a","b","c","x","x","x"], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
Output: 27
Explanation:
Score  a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax" (4+5), "bx" (4+5) and "cx" (4+5) with a score of 27.
Word "xxxz" only get a score of 25.

Example 3:

1
2
3
4

Input: words = ["leetcode"], letters = ["l","e","t","c","o","d"], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
Output: 0
Explanation:
Letter "e" can only be used once.

Solution

Method 1 - Backtracking

We start in a similar way to Subsets, and try to form set of words.

Here is the video explanation:

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    public int maxScoreWords(String[] words, char[] letters, int[] score) {
        int[] count = new int[score.length];
        for (char ch : letters) {
            count[ch - 'a']++;
        }
        return backtrack(words, count, score, 0);
    }
    int backtrack(String[] words, int[] count, int[] score, int idx) {
        if (idx == words.length) {
	        return 0;
        }
		int ans = 0;
		int curr = 0;
		boolean isValid = true;
		for (char ch : words[idx].toCharArray()) {
			count[ch - 'a']--;
			curr += score[ch - 'a'];
			if (count[ch - 'a'] < 0) {
				isValid = false;
			}
		}
		if (isValid) {
			// include
			ans = backtrack(words, count, score, idx + 1) + curr;
		}
		// revert counts array
		for (char ch : words[idx].toCharArray()) {
			count[ch - 'a']++;
		}
		ans = Math.max(ans, backtrack(words, count, score, idx + 1));
        
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public int maxScoreWords(String[] words, char[] letters, int[] score) {
        int[] count = new int[score.length];
        for (char ch : letters) {
            count[ch - 'a']++;
        }
        return backtrack(words, count, score, 0);
    }
    int backtrack(String[] words, int[] count, int[] score, int idx) {
        int ans = 0;
        for (int i = idx; i < words.length; i++) {
            int curr = 0;
            boolean isValid = true;
            for (char ch : words[i].toCharArray()) {
                count[ch - 'a']--;
                curr += score[ch - 'a'];
                if (count[ch - 'a'] < 0) {
	                isValid = false;
	            }
            }
            if (isValid) {
                curr += backtrack(words, count, score, i + 1);
                ans = Math.max(ans, curr);
            }
            for (char ch : words[i].toCharArray()) {
                count[ch - 'a']++;
                curr = 0;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n*l*2^n) - n - number of words, l - average length of the words. (We also change count array, but that multiplies time complexity by 26, which is constant).
  • 🧺 Space complexity: O(n)

Dry Run

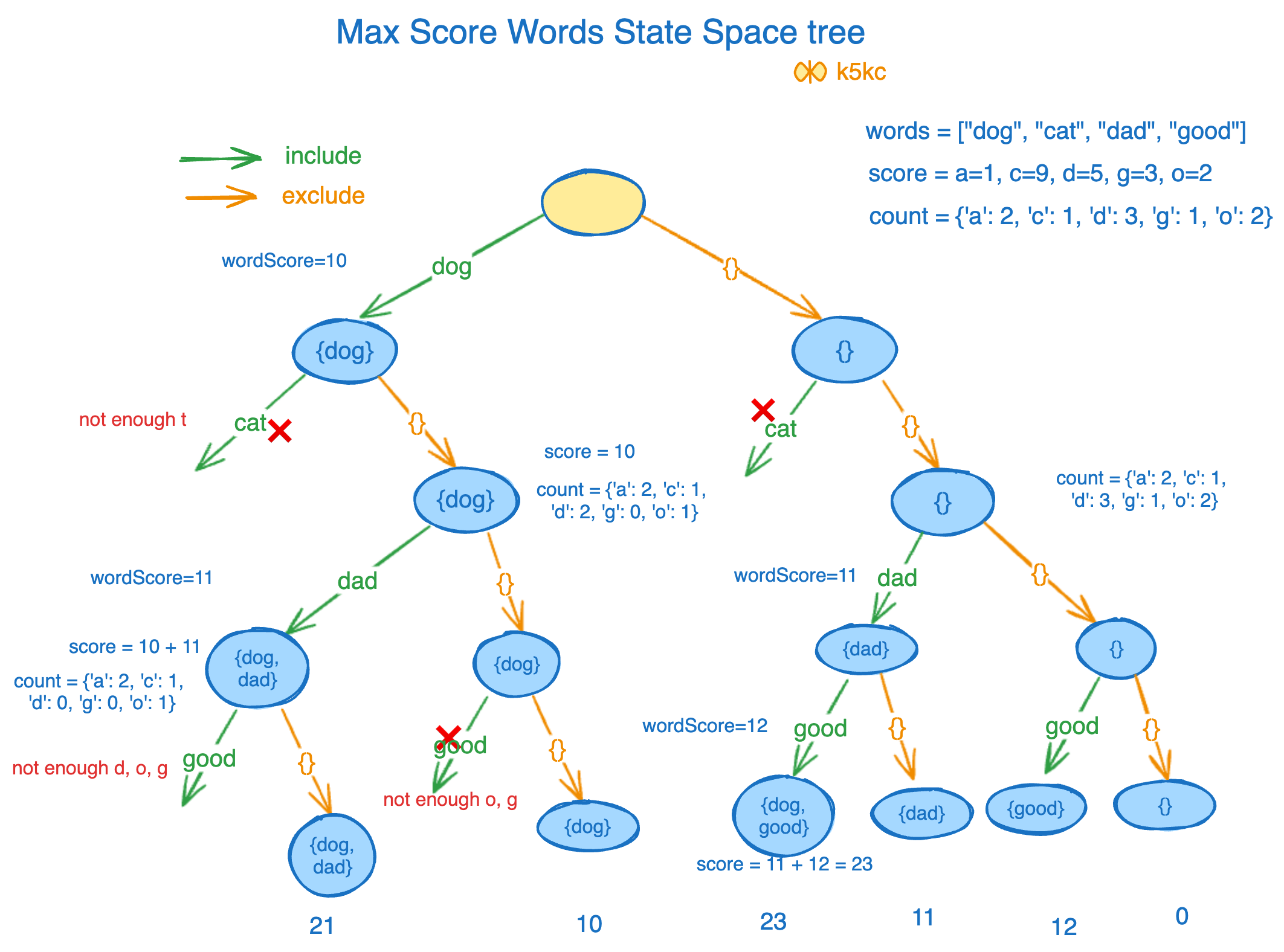
We start first by creating frequency map (count array) for given letters. count array initially: {'a': 2, 'c': 1, 'd': 3, 'g': 1, 'o': 2}.

Lets calculate the score of each word, for our understanding, assuming we are able to form it:

idx = 0, Word = “dog”
  • “dog” can be formed using {'d': 1, 'o': 1, 'g': 1}
  • Score: 5 + 2 + 3 = 10
  • count = {'a': 2, 'c': 1, 'd': 2, 'g': 0, 'o': 1}
idx = 1, Word = “cat”
  • “cat” cannot be formed (not enough ’t’), so we skip
idx = 2, Word = “dad”
  • “dad” can be formed using {'d': 2, 'a': 1}
  • Score: 5 + 1 + 5 = 11.
  • count = {'a': 1, 'c': 1, 'd': 1, 'g': 1, 'o': 2}
idx = 3, Word = “good”
  • “good” can be formed using {‘g’: 1, ‘o’: 2, ’d’: 1}
  • Score: 3 + 0 + 0 + 3 = 6
  • count = {'a': 2, 'c': 1, 'd': 2, 'g': 0, 'o': 0}
Recursive depth from different levels

We start with idx = 0.

We now start DFS on words = ["dog","cat","dad","good"].