Maximum Square Area by Removing Fences From a Field

Problem

There is a large (m - 1) x (n - 1) rectangular field with corners at (1, 1) and (m, n) containing some horizontal and vertical fences given in arrays hFences and vFences respectively.

Horizontal fences are from the coordinates (hFences[i], 1) to (hFences[i], n) and vertical fences are from the coordinates (1, vFences[i]) to (m, vFences[i]).

Return _themaximum area of a square field that can be formed by removing some fences (possibly none) or _-1 if it is impossible to make a square field.

Since the answer may be large, return it modulo 10^9 + 7.

Note: The field is surrounded by two horizontal fences from the coordinates (1, 1) to (1, n) and (m, 1) to (m, n) and two vertical fences from the coordinates (1, 1) to (m, 1) and (1, n) to (m, n). These fences cannot be removed.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2023/11/05/screenshot-
from-2023-11-05-22-40-25.png)

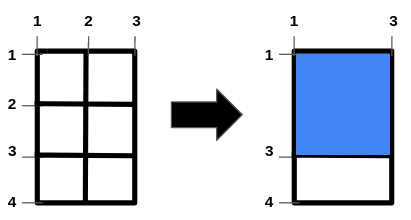
Input: m = 4, n = 3, hFences = [2,3], vFences = [2]
Output: 4
Explanation: Removing the horizontal fence at 2 and the vertical fence at 2 will give a square field of area 4.

Example 2

![](https://assets.leetcode.com/uploads/2023/11/22/maxsquareareaexample1.png)

Input: m = 6, n = 7, hFences = [2], vFences = [4]
Output: -1
Explanation: It can be proved that there is no way to create a square field by removing fences.

Constraints

• 3 <= m, n <= 10^9
• 1 <= hFences.length, vFences.length <= 600
• 1 < hFences[i] < m
• 1 < vFences[i] < n
• hFences and vFences are unique.

Solution

Method 1 – Hash Set for Distance Matching

Intuition

The largest square area is determined by the largest distance that appears as both a horizontal and vertical gap between fences. By removing fences, we can create larger gaps. We want the largest distance that is present in both the set of possible horizontal and vertical gaps.

Approach

1. Add the field boundaries (1 and m for horizontal, 1 and n for vertical) to the fence lists, then sort them.
2. Compute all possible distances between pairs of horizontal fences and store them in a set.
3. Do the same for vertical fences.
4. The answer is the largest distance that appears in both sets (since a square needs equal width and height).
5. If no such distance exists, return -1. Otherwise, return the square of the distance modulo 1e9+7.

Code

C++

class Solution {
public:
    int maxSquareArea(int m, int n, vector<int>& hFences, vector<int>& vFences) {
        hFences.push_back(1); hFences.push_back(m);
        vFences.push_back(1); vFences.push_back(n);
        sort(hFences.begin(), hFences.end());
        sort(vFences.begin(), vFences.end());
        unordered_set<int> hSet, vSet;
        for (int i = 0; i < hFences.size(); ++i)
            for (int j = i+1; j < hFences.size(); ++j)
                hSet.insert(hFences[j] - hFences[i]);
        for (int i = 0; i < vFences.size(); ++i)
            for (int j = i+1; j < vFences.size(); ++j)
                vSet.insert(vFences[j] - vFences[i]);
        int ans = -1;
        for (int d : hSet) if (vSet.count(d)) ans = max(ans, d);
        if (ans == -1) return -1;
        return (1LL * ans * ans) % 1000000007;
    }
};

Go

func maxSquareArea(m, n int, hFences, vFences []int) int {
    hFences = append(hFences, 1, m)
    vFences = append(vFences, 1, n)
    sort.Ints(hFences)
    sort.Ints(vFences)
    hSet, vSet := map[int]struct{}{}, map[int]struct{}{}
    for i := 0; i < len(hFences); i++ {
        for j := i+1; j < len(hFences); j++ {
            hSet[hFences[j]-hFences[i]] = struct{}{}
        }
    }
    for i := 0; i < len(vFences); i++ {
        for j := i+1; j < len(vFences); j++ {
            vSet[vFences[j]-vFences[i]] = struct{}{}
        }
    }
    ans := -1
    for d := range hSet {
        if _, ok := vSet[d]; ok && d > ans {
            ans = d
        }
    }
    if ans == -1 {
        return -1
    }
    return (ans * ans) % 1000000007
}

Java

class Solution {
    public int maxSquareArea(int m, int n, int[] hFences, int[] vFences) {
        List<Integer> h = new ArrayList<>();
        List<Integer> v = new ArrayList<>();
        for (int x : hFences) h.add(x);
        for (int x : vFences) v.add(x);
        h.add(1); h.add(m);
        v.add(1); v.add(n);
        Collections.sort(h); Collections.sort(v);
        Set<Integer> hSet = new HashSet<>(), vSet = new HashSet<>();
        for (int i = 0; i < h.size(); i++)
            for (int j = i+1; j < h.size(); j++)
                hSet.add(h.get(j) - h.get(i));
        for (int i = 0; i < v.size(); i++)
            for (int j = i+1; j < v.size(); j++)
                vSet.add(v.get(j) - v.get(i));
        int ans = -1;
        for (int d : hSet) if (vSet.contains(d)) ans = Math.max(ans, d);
        if (ans == -1) return -1;
        return (int)(((long)ans * ans) % 1000000007);
    }
}

Kotlin

class Solution {
    fun maxSquareArea(m: Int, n: Int, hFences: IntArray, vFences: IntArray): Int {
        val h = hFences.toMutableList().apply { add(1); add(m) }.sorted()
        val v = vFences.toMutableList().apply { add(1); add(n) }.sorted()
        val hSet = mutableSetOf<Int>()
        val vSet = mutableSetOf<Int>()
        for (i in h.indices) for (j in i+1 until h.size) hSet.add(h[j] - h[i])
        for (i in v.indices) for (j in i+1 until v.size) vSet.add(v[j] - v[i])
        val ans = hSet.filter { it in vSet }.maxOrNull() ?: -1
        return if (ans == -1) -1 else ((ans.toLong() * ans) % 1000000007L).toInt()
    }
}

Python

class Solution:
    def maxSquareArea(self, m: int, n: int, hFences: list[int], vFences: list[int]) -> int:
        hFences = sorted(hFences + [1, m])
        vFences = sorted(vFences + [1, n])
        hSet = set()
        vSet = set()
        for i in range(len(hFences)):
            for j in range(i+1, len(hFences)):
                hSet.add(hFences[j] - hFences[i])
        for i in range(len(vFences)):
            for j in range(i+1, len(vFences)):
                vSet.add(vFences[j] - vFences[i])
        ans = max((d for d in hSet if d in vSet), default=-1)
        return -1 if ans == -1 else (ans * ans) % 1_000_000_007

Rust

use std::collections::HashSet;
impl Solution {
    pub fn max_square_area(m: i32, n: i32, mut h: Vec<i32>, mut v: Vec<i32>) -> i32 {
        h.push(1); h.push(m);
        v.push(1); v.push(n);
        h.sort(); v.sort();
        let mut hset = HashSet::new();
        let mut vset = HashSet::new();
        for i in 0..h.len() {
            for j in i+1..h.len() {
                hset.insert(h[j] - h[i]);
            }
        }
        for i in 0..v.len() {
            for j in i+1..v.len() {
                vset.insert(v[j] - v[i]);
            }
        }
        let mut ans = -1;
        for &d in &hset {
            if vset.contains(&d) && d > ans {
                ans = d;
            }
        }
        if ans == -1 { -1 } else { ((ans as i64 * ans as i64) % 1_000_000_007) as i32 }
    }
}

TypeScript

class Solution {
    maxSquareArea(m: number, n: number, hFences: number[], vFences: number[]): number {
        hFences = [...hFences, 1, m].sort((a, b) => a - b);
        vFences = [...vFences, 1, n].sort((a, b) => a - b);
        const hSet = new Set<number>(), vSet = new Set<number>();
        for (let i = 0; i < hFences.length; ++i)
            for (let j = i+1; j < hFences.length; ++j)
                hSet.add(hFences[j] - hFences[i]);
        for (let i = 0; i < vFences.length; ++i)
            for (let j = i+1; j < vFences.length; ++j)
                vSet.add(vFences[j] - vFences[i]);
        let ans = -1;
        for (const d of hSet) if (vSet.has(d) && d > ans) ans = d;
        return ans === -1 ? -1 : (ans * ans) % 1_000_000_007;
    }
}

Complexity

• ⏰ Time complexity: O((h^2 + v^2)), where h and v are the number of horizontal and vertical fences. Each pair is checked for all possible distances.
• 🧺 Space complexity: O(h^2 + v^2), for the sets of all possible distances.