Maximum Sum BST in Binary Tree

Problem

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Examples

Example 1

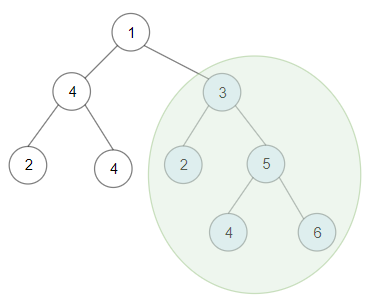
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2

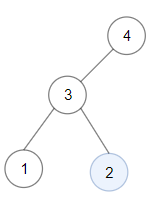
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Constraints

• The number of nodes in the tree is in the range [1, 4 * 10^4].
• -4 * 10^4 <= Node.val <= 4 * 10^4

Solution

Method 1 – Postorder Traversal with State Tracking

Intuition

To find the maximum sum BST in a binary tree, we need to check every subtree to see if it is a BST and calculate its sum. By traversing the tree in postorder, we can gather information from the left and right subtrees before making decisions at the current node.

Approach

1. Use postorder traversal to visit each node after its children.
2. For each node, collect:
   • Whether its left and right subtrees are BSTs.
   • The minimum and maximum values in its subtrees.
   • The sum of its subtree if it is a BST.
3. If the current node forms a BST with its children, update the global maximum sum.
4. If not a BST, propagate invalid state upwards.
5. Return the maximum sum found.

Code

C++

struct TreeNode {
    int val;
    TreeNode *left, *right;
};
class Solution {
public:
    int ans = 0;
    vector<int> dfs(TreeNode* node) {
        if (!node) return {1, INT_MAX, INT_MIN, 0};
        auto l = dfs(node->left), r = dfs(node->right);
        if (l[0] && r[0] && node->val > l[2] && node->val < r[1]) {
            int sum = l[3] + r[3] + node->val;
            ans = max(ans, sum);
            return {1, min(l[1], node->val), max(r[2], node->val), sum};
        }
        return {0, 0, 0, 0};
    }
    int maxSumBST(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

Go

type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func maxSumBST(root *TreeNode) int {
    ans := 0
    var dfs func(*TreeNode) (bool, int, int, int)
    dfs = func(node *TreeNode) (bool, int, int, int) {
        if node == nil {
            return true, 1<<31-1, -1<<31, 0
        }
        lbst, lmin, lmax, lsum := dfs(node.Left)
        rbst, rmin, rmax, rsum := dfs(node.Right)
        if lbst && rbst && node.Val > lmax && node.Val < rmin {
            sum := lsum + rsum + node.Val
            if sum > ans {
                ans = sum
            }
            minv := lmin
            if node.Val < minv {
                minv = node.Val
            }
            maxv := rmax
            if node.Val > maxv {
                maxv = node.Val
            }
            return true, minv, maxv, sum
        }
        return false, 0, 0, 0
    }
    dfs(root)
    return ans
}

Java

class TreeNode {
    int val;
    TreeNode left, right;
}
class Solution {
    int ans = 0;
    int[] dfs(TreeNode node) {
        if (node == null) return new int[]{1, Integer.MAX_VALUE, Integer.MIN_VALUE, 0};
        int[] l = dfs(node.left), r = dfs(node.right);
        if (l[0]==1 && r[0]==1 && node.val > l[2] && node.val < r[1]) {
            int sum = l[3] + r[3] + node.val;
            ans = Math.max(ans, sum);
            return new int[]{1, Math.min(l[1], node.val), Math.max(r[2], node.val), sum};
        }
        return new int[]{0, 0, 0, 0};
    }
    public int maxSumBST(TreeNode root) {
        dfs(root);
        return ans;
    }
}

Kotlin

data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    var ans = 0
    fun dfs(node: TreeNode?): IntArray {
        if (node == null) return intArrayOf(1, Int.MAX_VALUE, Int.MIN_VALUE, 0)
        val l = dfs(node.left)
        val r = dfs(node.right)
        if (l[0]==1 && r[0]==1 && node.`val` > l[2] && node.`val` < r[1]) {
            val sum = l[3] + r[3] + node.`val`
            ans = maxOf(ans, sum)
            return intArrayOf(1, minOf(l[1], node.`val`), maxOf(r[2], node.`val`), sum)
        }
        return intArrayOf(0, 0, 0, 0)
    }
    fun maxSumBST(root: TreeNode?): Int {
        dfs(root)
        return ans
    }
}

Python

class TreeNode:
    def __init__(self, val: int, left: 'TreeNode' = None, right: 'TreeNode' = None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def maxSumBST(self, root: TreeNode) -> int:
        ans = 0
        def dfs(node: TreeNode) -> tuple[int, int, int, int]:
            if not node:
                return 1, float('inf'), float('-inf'), 0
            lbst, lmin, lmax, lsum = dfs(node.left)
            rbst, rmin, rmax, rsum = dfs(node.right)
            if lbst and rbst and node.val > lmax and node.val < rmin:
                s = lsum + rsum + node.val
                nonlocal ans
                ans = max(ans, s)
                return 1, min(lmin, node.val), max(rmax, node.val), s
            return 0, 0, 0, 0
        dfs(root)
        return ans

Rust

pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn max_sum_bst(root: Option<Box<TreeNode>>) -> i32 {
        fn dfs(node: &Option<Box<TreeNode>>, ans: &mut i32) -> (bool, i32, i32, i32) {
            if let Some(n) = node {
                let (lbst, lmin, lmax, lsum) = dfs(&n.left, ans);
                let (rbst, rmin, rmax, rsum) = dfs(&n.right, ans);
                if lbst && rbst && n.val > lmax && n.val < rmin {
                    let sum = lsum + rsum + n.val;
                    *ans = (*ans).max(sum);
                    return (true, lmin.min(n.val), rmax.max(n.val), sum);
                }
                (false, 0, 0, 0)
            } else {
                (true, i32::MAX, i32::MIN, 0)
            }
        }
        let mut ans = 0;
        dfs(&root, &mut ans);
        ans
    }
}

TypeScript

class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val ?? 0;
        this.left = left ?? null;
        this.right = right ?? null;
    }
}
class Solution {
    ans = 0;
    dfs(node: TreeNode | null): [boolean, number, number, number] {
        if (!node) return [true, Infinity, -Infinity, 0];
        const [lbst, lmin, lmax, lsum] = this.dfs(node.left);
        const [rbst, rmin, rmax, rsum] = this.dfs(node.right);
        if (lbst && rbst && node.val > lmax && node.val < rmin) {
            const sum = lsum + rsum + node.val;
            this.ans = Math.max(this.ans, sum);
            return [true, Math.min(lmin, node.val), Math.max(rmax, node.val), sum];
        }
        return [false, 0, 0, 0];
    }
    maxSumBST(root: TreeNode | null): number {
        this.dfs(root);
        return this.ans;
    }
}

Complexity

• ⏰ Time complexity: O(n), since each node is visited once.
• 🧺 Space complexity: O(h), where h is the height of the tree due to recursion stack.