Problem

You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.

You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.

Return themaximum number of white tiles that can be covered by the carpet.

Examples

Example 1

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2022/03/25/example1drawio3.png)

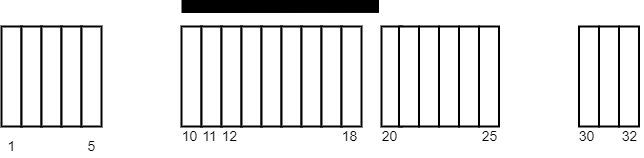
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
Output: 9
Explanation: Place the carpet starting on tile 10. 
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.

Example 2

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2022/03/24/example2drawio.png)

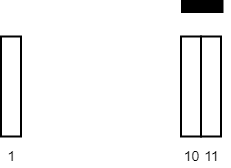
Input: tiles = [[10,11],[1,1]], carpetLen = 2
Output: 2
Explanation: Place the carpet starting on tile 10. 
It covers 2 white tiles, so we return 2.

Constraints

  • 1 <= tiles.length <= 5 * 10^4
  • tiles[i].length == 2
  • 1 <= li <= ri <= 10^9
  • 1 <= carpetLen <= 10^9
  • The tiles are non-overlapping.

Solution

Method 1 – Sliding Window with Binary Search

Intuition

To maximize the number of white tiles covered, sort the tiles and use a sliding window to try placing the carpet starting at each tile. For each start, use binary search to find the last tile the carpet can reach, and calculate the total coverage.

Approach

  1. Sort the tiles by their starting position.
  2. For each tile, consider placing the carpet starting at its left end.
  3. Use binary search to find the last tile whose left end is within the carpet’s reach.
  4. Calculate the total covered tiles:
    • Sum the lengths of all fully covered tiles in the window.
    • For the last tile, only count the part covered by the carpet.
  5. Track and return the maximum coverage found.

Complexity

  • ⏰ Time complexity: O(n log n) — Sorting and binary search for each tile.
  • 🧺 Space complexity: O(n) — For prefix sums and sorted tiles.
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end());
        int n = tiles.size(), ans = 0;
        vector<int> prefix(n+1);
        for (int i = 0; i < n; ++i)
            prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1;
        for (int i = 0; i < n; ++i) {
            int end = tiles[i][0] + carpetLen - 1;
            int l = i, r = n-1, j = i;
            while (l <= r) {
                int m = (l + r) / 2;
                if (tiles[m][0] <= end) { j = m; l = m + 1; }
                else r = m - 1;
            }
            int covered = prefix[j] - prefix[i];
            int last = min(end, tiles[j][1]);
            covered += max(0, last - tiles[j][0] + 1);
            ans = max(ans, covered);
        }
        return ans;
    }
};
Go
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

func maximumWhiteTiles(tiles [][]int, carpetLen int) int {
    sort.Slice(tiles, func(i, j int) bool { return tiles[i][0] < tiles[j][0] })
    n := len(tiles)
    prefix := make([]int, n+1)
    for i := 0; i < n; i++ {
        prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1
    }
    ans := 0
    for i := 0; i < n; i++ {
        end := tiles[i][0] + carpetLen - 1
        l, r, j := i, n-1, i
        for l <= r {
            m := (l + r) / 2
            if tiles[m][0] <= end { j = m; l = m + 1 } else { r = m - 1 }
        }
        covered := prefix[j] - prefix[i]
        last := end
        if last > tiles[j][1] { last = tiles[j][1] }
        covered += max(0, last - tiles[j][0] + 1)
        if covered > ans { ans = covered }
    }
    return ans
}
func max(a, b int) int { if a > b { return a } else { return b } }
Java
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
    public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
        Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
        int n = tiles.length, ans = 0;
        int[] prefix = new int[n+1];
        for (int i = 0; i < n; ++i)
            prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1;
        for (int i = 0; i < n; ++i) {
            int end = tiles[i][0] + carpetLen - 1;
            int l = i, r = n-1, j = i;
            while (l <= r) {
                int m = (l + r) / 2;
                if (tiles[m][0] <= end) { j = m; l = m + 1; }
                else r = m - 1;
            }
            int covered = prefix[j] - prefix[i];
            int last = Math.min(end, tiles[j][1]);
            covered += Math.max(0, last - tiles[j][0] + 1);
            ans = Math.max(ans, covered);
        }
        return ans;
    }
}
Kotlin
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    fun maximumWhiteTiles(tiles: Array<IntArray>, carpetLen: Int): Int {
        tiles.sortBy { it[0] }
        val n = tiles.size
        val prefix = IntArray(n+1)
        for (i in 0 until n) prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1
        var ans = 0
        for (i in 0 until n) {
            val end = tiles[i][0] + carpetLen - 1
            var l = i; var r = n-1; var j = i
            while (l <= r) {
                val m = (l + r) / 2
                if (tiles[m][0] <= end) { j = m; l = m + 1 } else r = m - 1
            }
            var covered = prefix[j] - prefix[i]
            val last = minOf(end, tiles[j][1])
            covered += maxOf(0, last - tiles[j][0] + 1)
            ans = maxOf(ans, covered)
        }
        return ans
    }
}
Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def maximum_white_tiles(tiles: list[list[int]], carpet_len: int) -> int:
    tiles.sort()
    n = len(tiles)
    prefix = [0] * (n+1)
    for i in range(n):
        prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1
    ans = 0
    for i in range(n):
        end = tiles[i][0] + carpet_len - 1
        l, r, j = i, n-1, i
        while l <= r:
            m = (l + r) // 2
            if tiles[m][0] <= end:
                j = m
                l = m + 1
            else:
                r = m - 1
        covered = prefix[j] - prefix[i]
        last = min(end, tiles[j][1])
        covered += max(0, last - tiles[j][0] + 1)
        ans = max(ans, covered)
    return ans
Rust
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

impl Solution {
    pub fn maximum_white_tiles(tiles: Vec<Vec<i32>>, carpet_len: i32) -> i32 {
        let mut tiles = tiles;
        tiles.sort_by_key(|x| x[0]);
        let n = tiles.len();
        let mut prefix = vec![0; n+1];
        for i in 0..n {
            prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1;
        }
        let mut ans = 0;
        for i in 0..n {
            let end = tiles[i][0] + carpet_len - 1;
            let (mut l, mut r, mut j) = (i, n-1, i);
            while l <= r {
                let m = (l + r) / 2;
                if tiles[m][0] <= end { j = m; l = m + 1; } else { r = m - 1; }
            }
            let mut covered = prefix[j] - prefix[i];
            let last = end.min(tiles[j][1]);
            covered += (last - tiles[j][0] + 1).max(0);
            ans = ans.max(covered);
        }
        ans
    }
}
TypeScript
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    maximumWhiteTiles(tiles: number[][], carpetLen: number): number {
        tiles.sort((a, b) => a[0] - b[0]);
        const n = tiles.length;
        const prefix = Array(n+1).fill(0);
        for (let i = 0; i < n; ++i)
            prefix[i+1] = prefix[i] + tiles[i][1] - tiles[i][0] + 1;
        let ans = 0;
        for (let i = 0; i < n; ++i) {
            const end = tiles[i][0] + carpetLen - 1;
            let l = i, r = n-1, j = i;
            while (l <= r) {
                const m = Math.floor((l + r) / 2);
                if (tiles[m][0] <= end) { j = m; l = m + 1; }
                else r = m - 1;
            }
            let covered = prefix[j] - prefix[i];
            const last = Math.min(end, tiles[j][1]);
            covered += Math.max(0, last - tiles[j][0] + 1);
            ans = Math.max(ans, covered);
        }
        return ans;
    }
}