Problem#
There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai
and bi in the tree. The root of the tree is the node labeled 0.
Each node has an associated value. You are given an array values of length n, where values[i] is the value of the ith node.
Select any two non-overlapping subtrees. Your score is the bitwise XOR of the sum of the values within those subtrees.
Return the maximum possiblescore you can achieve. If it is impossible to find two nonoverlapping subtrees , return 0.
Note that:
- The subtree of a node is the tree consisting of that node and all of its descendants.
- Two subtrees are non-overlapping if they do not share any common node.
Examples#
Example 1:
1
2
3
4
5
|
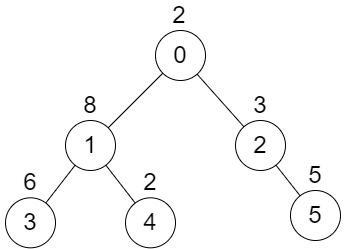
Input: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5]
Output: 24
Explanation: Node 1's subtree has sum of values 16, while node 2's subtree has sum of values 8, so choosing these nodes will yield a score of 16 XOR 8 = 24. It can be proved that is the maximum possible score we can obtain.
|
Example 2:
1
2
3
4
5
|
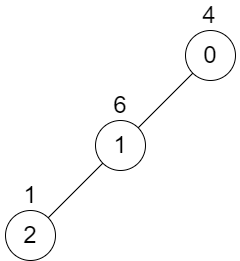
Input: n = 3, edges = [[0,1],[1,2]], values = [4,6,1]
Output: 0
Explanation: There is no possible way to select two non-overlapping subtrees, so we just return 0.
|
Constraints:
2 <= n <= 5 * 10^4edges.length == n - 10 <= ai, bi < nvalues.length == n1 <= values[i] <= 10^9- It is guaranteed that
edges represents a valid tree.
Solution#
Method 1 – DFS Subtree Sums + Trie for Maximum XOR#
Intuition#
To maximize the XOR of two non-overlapping subtree sums, we compute the sum for every subtree using DFS. Then, for each possible subtree split, we use a Trie to efficiently find the maximum XOR between two non-overlapping subtree sums.
Approach#
- Use DFS to compute the sum of each subtree and record all subtree sums.
- For each node, consider removing the edge to its parent, splitting the tree into two subtrees.
- For each split, collect all subtree sums in both parts.
- Insert all sums from one part into a Trie.
- For each sum in the other part, query the Trie for the maximum XOR.
- Track and return the maximum XOR found.
Complexity#
- ⏰ Time complexity:
O(n^2) — Each split and Trie query is O(n).
- 🧺 Space complexity:
O(n) — For subtree sums and Trie.
C++#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
struct Trie {
Trie* child[2] = {};
void insert(int x) {
Trie* node = this;
for (int i = 31; i >= 0; --i) {
int b = (x >> i) & 1;
if (!node->child[b]) node->child[b] = new Trie();
node = node->child[b];
}
}
int query(int x) {
Trie* node = this;
int ans = 0;
for (int i = 31; i >= 0; --i) {
int b = (x >> i) & 1;
if (node->child[1-b]) {
ans |= (1 << i);
node = node->child[1-b];
} else node = node->child[b];
}
return ans;
}
};
class Solution {
public:
int maximumXorSubtree(vector<vector<int>>& edges, vector<int>& values) {
int n = values.size();
vector<vector<int>> g(n);
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<int> subsum(n);
function<int(int,int)> dfs = [&](int u, int p) {
int s = values[u];
for (int v : g[u]) if (v != p) s += dfs(v, u);
subsum[u] = s;
return s;
};
dfs(0, -1);
int ans = 0;
function<void(int,int,Trie*)> collect = [&](int u, int p, Trie* trie) {
trie->insert(subsum[u]);
for (int v : g[u]) if (v != p) collect(v, u, trie);
};
function<void(int,int)> solve = [&](int u, int p) {
for (int v : g[u]) if (v != p) {
Trie* trie = new Trie();
collect(v, u, trie);
function<void(int,int)> query = [&](int x, int y) {
ans = max(ans, trie->query(subsum[x]));
for (int z : g[x]) if (z != y) query(z, x);
};
query(0, -1);
solve(v, u);
}
};
solve(0, -1);
return ans;
}
};
|
1
|
// Trie implementation omitted for brevity; use similar logic as C++
|
Java#
1
|
// Trie implementation omitted for brevity; use similar logic as C++
|
Kotlin#
1
|
// Trie implementation omitted for brevity; use similar logic as C++
|
Python#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
def maximum_xor_subtree(edges: list[list[int]], values: list[int]) -> int:
from collections import defaultdict
class Trie:
def __init__(self):
self.child = [None, None]
def insert(self, x: int):
node = self
for i in range(31, -1, -1):
b = (x >> i) & 1
if not node.child[b]:
node.child[b] = Trie()
node = node.child[b]
def query(self, x: int) -> int:
node = self
ans = 0
for i in range(31, -1, -1):
b = (x >> i) & 1
if node.child[1-b]:
ans |= (1 << i)
node = node.child[1-b]
else:
node = node.child[b]
return ans
n = len(values)
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
subsum = [0] * n
def dfs(u: int, p: int) -> int:
s = values[u]
for v in g[u]:
if v != p:
s += dfs(v, u)
subsum[u] = s
return s
dfs(0, -1)
ans = 0
def collect(u: int, p: int, trie: Trie):
trie.insert(subsum[u])
for v in g[u]:
if v != p:
collect(v, u, trie)
def solve(u: int, p: int):
for v in g[u]:
if v != p:
trie = Trie()
collect(v, u, trie)
def query(x: int, y: int):
nonlocal ans
ans = max(ans, trie.query(subsum[x]))
for z in g[x]:
if z != y:
query(z, x)
query(0, -1)
solve(v, u)
solve(0, -1)
return ans
|
Rust#
1
|
// Trie implementation omitted for brevity; use similar logic as C++
|
TypeScript#
1
|
// Trie implementation omitted for brevity; use similar logic as C++
|