problemhardalgorithmsleetcode-1932leetcode 1932leetcode1932

Merge BSTs to Create Single BST

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given n BST (binary search tree) root nodes for n separate BSTs stored in an array trees (0-indexed). Each BST in trees has at most 3 nodes , and no two roots have the same value. In one operation, you can:

  • Select two distinct indices i and j such that the value stored at one of the leaves of trees[i] is equal to the root value of trees[j].
  • Replace the leaf node in trees[i] with trees[j].
  • Remove trees[j] from trees.

Return _theroot of the resulting BST if it is possible to form a valid BST after performing _n - 1 operations, or __null if it is impossible to create a valid BST.

A BST (binary search tree) is a binary tree where each node satisfies the following property:

  • Every node in the node's left subtree has a value strictly less than the node's value.
  • Every node in the node's right subtree has a value strictly greater than the node's value.

A leaf is a node that has no children.

Examples

Example 1


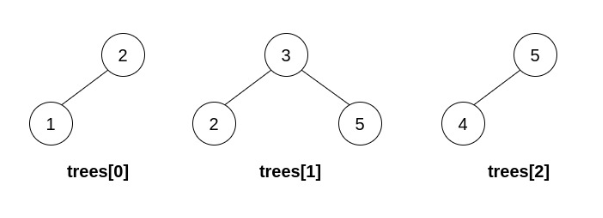
![](https://assets.leetcode.com/uploads/2021/06/08/d1.png)

Input: trees = [[2,1],[3,2,5],[5,4]]
Output: [3,2,5,1,null,4]
Explanation:
In the first operation, pick i=1 and j=0, and merge trees[0] into trees[1].
Delete trees[0], so trees = [[3,2,5,1],[5,4]].
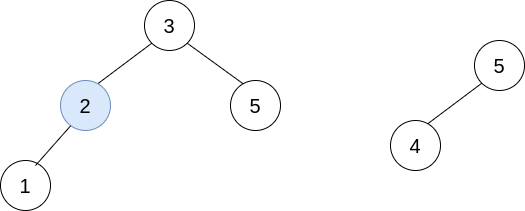
![](https://assets.leetcode.com/uploads/2021/06/24/diagram.png)
In the second operation, pick i=0 and j=1, and merge trees[1] into trees[0].
Delete trees[1], so trees = [[3,2,5,1,null,4]].
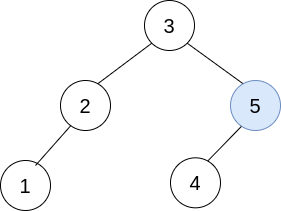
![](https://assets.leetcode.com/uploads/2021/06/24/diagram-2.png)
The resulting tree, shown above, is a valid BST, so return its root.

Example 2


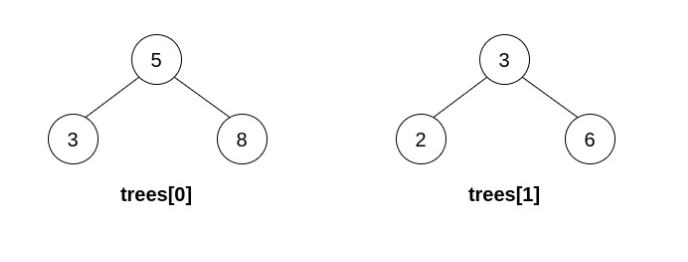
![](https://assets.leetcode.com/uploads/2021/06/08/d2.png)

Input: trees = [[5,3,8],[3,2,6]]
Output: []
Explanation:
Pick i=0 and j=1 and merge trees[1] into trees[0].
Delete trees[1], so trees = [[5,3,8,2,6]].
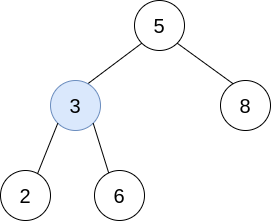
![](https://assets.leetcode.com/uploads/2021/06/24/diagram-3.png)
The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.

Example 3


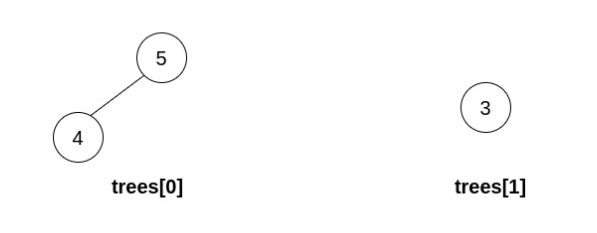
![](https://assets.leetcode.com/uploads/2021/06/08/d3.png)

Input: trees = [[5,4],[3]]
Output: []
Explanation: It is impossible to perform any operations.

Constraints

  • n == trees.length
  • 1 <= n <= 5 * 10^4
  • The number of nodes in each tree is in the range [1, 3].
  • Each node in the input may have children but no grandchildren.
  • No two roots of trees have the same value.
  • All the trees in the input are valid BSTs.
  • 1 <= TreeNode.val <= 5 * 10^4.

Solution

Method 1 – Hash Mapping and DFS Merge

Intuition

Since each BST has at most 3 nodes and no two roots have the same value, we can use a hash map to quickly find which tree can be merged at a leaf. By recursively merging trees at leaves, we can attempt to build a single BST. After merging, we must check if the result is a valid BST and contains all nodes.

Approach

  1. Build a map from root value to tree for quick lookup.
  2. For each tree, count leaf values and root values to find the unique root (the one not referenced as a leaf).
  3. Starting from the unique root, recursively merge trees at leaves using DFS.
  4. After merging, check if the resulting tree is a valid BST and contains all nodes.
  5. If valid, return the root; otherwise, return null.

Code

C++
struct TreeNode {
    int val;
    TreeNode *left, *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    TreeNode* canMerge(vector<TreeNode*>& trees) {
        unordered_map<int, TreeNode*> mp;
        unordered_map<int, int> leafCount;
        for (auto t : trees) {
            mp[t->val] = t;
            if (t->left) leafCount[t->left->val]++;
            if (t->right) leafCount[t->right->val]++;
        }
        TreeNode* root = nullptr;
        for (auto t : trees) {
            if (!leafCount.count(t->val)) {
                root = t;
                break;
            }
        }
        if (!root) return nullptr;
        unordered_set<int> used;
        function<TreeNode*(TreeNode*)> dfs = [&](TreeNode* node) -> TreeNode* {
            if (!node) return nullptr;
            if (mp.count(node->val) && node != root && !used.count(node->val)) {
                used.insert(node->val);
                node = mp[node->val];
            }
            node->left = dfs(node->left);
            node->right = dfs(node->right);
            return node;
        };
        root = dfs(root);
        int total = 0;
        function<bool(TreeNode*, int, int)> valid = [&](TreeNode* node, int mn, int mx) -> bool {
            if (!node) return true;
            if (node->val <= mn || node->val >= mx) return false;
            total++;
            return valid(node->left, mn, node->val) && valid(node->right, node->val, mx);
        };
        if (!valid(root, INT_MIN, INT_MAX) || total != trees.size() * 3) return nullptr;
        return root;
    }
};
Go
type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func canMerge(trees []*TreeNode) *TreeNode {
    mp := map[int]*TreeNode{}
    leafCount := map[int]int{}
    for _, t := range trees {
        mp[t.Val] = t
        if t.Left != nil { leafCount[t.Left.Val]++ }
        if t.Right != nil { leafCount[t.Right.Val]++ }
    }
    var root *TreeNode
    for _, t := range trees {
        if leafCount[t.Val] == 0 {
            root = t
            break
        }
    }
    if root == nil { return nil }
    used := map[int]bool{}
    var dfs func(*TreeNode) *TreeNode
    dfs = func(node *TreeNode) *TreeNode {
        if node == nil { return nil }
        if mp[node.Val] != nil && node != root && !used[node.Val] {
            used[node.Val] = true
            node = mp[node.Val]
        }
        node.Left = dfs(node.Left)
        node.Right = dfs(node.Right)
        return node
    }
    root = dfs(root)
    total := 0
    var valid func(*TreeNode, int, int) bool
    valid = func(node *TreeNode, mn, mx int) bool {
        if node == nil { return true }
        if node.Val <= mn || node.Val >= mx { return false }
        total++
        return valid(node.Left, mn, node.Val) && valid(node.Right, node.Val, mx)
    }
    if !valid(root, -1<<31, 1<<31-1) || total != len(trees)*3 { return nil }
    return root
}
Java
class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    public TreeNode canMerge(List<TreeNode> trees) {
        Map<Integer, TreeNode> mp = new HashMap<>();
        Map<Integer, Integer> leafCount = new HashMap<>();
        for (TreeNode t : trees) {
            mp.put(t.val, t);
            if (t.left != null) leafCount.put(t.left.val, leafCount.getOrDefault(t.left.val, 0) + 1);
            if (t.right != null) leafCount.put(t.right.val, leafCount.getOrDefault(t.right.val, 0) + 1);
        }
        TreeNode root = null;
        for (TreeNode t : trees) {
            if (!leafCount.containsKey(t.val)) {
                root = t;
                break;
            }
        }
        if (root == null) return null;
        Set<Integer> used = new HashSet<>();
        root = dfs(root, mp, used, root);
        int[] total = new int[1];
        if (!valid(root, Integer.MIN_VALUE, Integer.MAX_VALUE, total) || total[0] != trees.size() * 3) return null;
        return root;
    }
    private TreeNode dfs(TreeNode node, Map<Integer, TreeNode> mp, Set<Integer> used, TreeNode root) {
        if (node == null) return null;
        if (mp.containsKey(node.val) && node != root && !used.contains(node.val)) {
            used.add(node.val);
            node = mp.get(node.val);
        }
        node.left = dfs(node.left, mp, used, root);
        node.right = dfs(node.right, mp, used, root);
        return node;
    }
    private boolean valid(TreeNode node, int mn, int mx, int[] total) {
        if (node == null) return true;
        if (node.val <= mn || node.val >= mx) return false;
        total[0]++;
        return valid(node.left, mn, node.val, total) && valid(node.right, node.val, mx, total);
    }
}
Kotlin
data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    fun canMerge(trees: List<TreeNode>): TreeNode? {
        val mp = mutableMapOf<Int, TreeNode>()
        val leafCount = mutableMapOf<Int, Int>()
        for (t in trees) {
            mp[t.`val`] = t
            t.left?.let { leafCount[it.`val`] = leafCount.getOrDefault(it.`val`, 0) + 1 }
            t.right?.let { leafCount[it.`val`] = leafCount.getOrDefault(it.`val`, 0) + 1 }
        }
        var root: TreeNode? = null
        for (t in trees) {
            if (!leafCount.containsKey(t.`val`)) {
                root = t
                break
            }
        }
        if (root == null) return null
        val used = mutableSetOf<Int>()
        fun dfs(node: TreeNode?): TreeNode? {
            if (node == null) return null
            if (mp.containsKey(node.`val`) && node != root && !used.contains(node.`val`)) {
                used.add(node.`val`)
                return mp[node.`val`]
            }
            node.left = dfs(node.left)
            node.right = dfs(node.right)
            return node
        }
        root = dfs(root)
        var total = 0
        fun valid(node: TreeNode?, mn: Int, mx: Int): Boolean {
            if (node == null) return true
            if (node.`val` <= mn || node.`val` >= mx) return false
            total++
            return valid(node.left, mn, node.`val`) && valid(node.right, node.`val`, mx)
        }
        if (!valid(root, Int.MIN_VALUE, Int.MAX_VALUE) || total != trees.size * 3) return null
        return root
    }
}
Python
class TreeNode:
    def __init__(self, val: int, left: 'TreeNode' = None, right: 'TreeNode' = None):
        self.val = val
        self.left = left
        self.right = right

def can_merge(trees: list['TreeNode']) -> 'TreeNode | None':
    mp = {t.val: t for t in trees}
    leaf_count = {}
    for t in trees:
        if t.left: leaf_count[t.left.val] = leaf_count.get(t.left.val, 0) + 1
        if t.right: leaf_count[t.right.val] = leaf_count.get(t.right.val, 0) + 1
    root = None
    for t in trees:
        if t.val not in leaf_count:
            root = t
            break
    if not root: return None
    used = set()
    def dfs(node):
        if not node: return None
        if node.val in mp and node != root and node.val not in used:
            used.add(node.val)
            node = mp[node.val]
        node.left = dfs(node.left)
        node.right = dfs(node.right)
        return node
    root = dfs(root)
    total = 0
    def valid(node, mn, mx):
        nonlocal total
        if not node: return True
        if node.val <= mn or node.val >= mx: return False
        total += 1
        return valid(node.left, mn, node.val) and valid(node.right, node.val, mx)
    if not valid(root, float('-inf'), float('inf')) or total != len(trees) * 3:
        return None
    return root
Rust
struct TreeNode {
    val: i32,
    left: Option<Box<TreeNode>>,
    right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn can_merge(trees: Vec<Box<TreeNode>>) -> Option<Box<TreeNode>> {
        use std::collections::{HashMap, HashSet};
        let mut mp = HashMap::new();
        let mut leaf_count = HashMap::new();
        for t in &trees {
            mp.insert(t.val, t);
            if let Some(ref l) = t.left { *leaf_count.entry(l.val).or_insert(0) += 1; }
            if let Some(ref r) = t.right { *leaf_count.entry(r.val).or_insert(0) += 1; }
        }
        let mut root = None;
        for t in &trees {
            if !leaf_count.contains_key(&t.val) {
                root = Some(t);
                break;
            }
        }
        let root = match root { Some(r) => r, None => return None };
        let mut used = HashSet::new();
        fn dfs(node: &Box<TreeNode>, mp: &HashMap<i32, &Box<TreeNode>>, used: &mut HashSet<i32>, root_val: i32) -> Box<TreeNode> {
            let mut node = node.clone();
            if mp.contains_key(&node.val) && node.val != root_val && !used.contains(&node.val) {
                used.insert(node.val);
                node = mp[&node.val].clone();
            }
            if let Some(ref l) = node.left { node.left = Some(dfs(l, mp, used, root_val)); }
            if let Some(ref r) = node.right { node.right = Some(dfs(r, mp, used, root_val)); }
            node
        }
        let mut root = dfs(root, &mp, &mut used, root.val);
        let mut total = 0;
        fn valid(node: &Option<Box<TreeNode>>, mn: i32, mx: i32, total: &mut i32) -> bool {
            if let Some(ref n) = node {
                if n.val <= mn || n.val >= mx { return false; }
                *total += 1;
                valid(&n.left, mn, n.val, total) && valid(&n.right, n.val, mx, total)
            } else { true }
        }
        if !valid(&Some(root.clone()), i32::MIN, i32::MAX, &mut total) || total != trees.len() * 3 { return None; }
        Some(root)
    }
}
TypeScript
class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val: number, left: TreeNode | null = null, right: TreeNode | null = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
class Solution {
    canMerge(trees: TreeNode[]): TreeNode | null {
        const mp = new Map<number, TreeNode>();
        const leafCount = new Map<number, number>();
        for (const t of trees) {
            mp.set(t.val, t);
            if (t.left) leafCount.set(t.left.val, (leafCount.get(t.left.val) ?? 0) + 1);
            if (t.right) leafCount.set(t.right.val, (leafCount.get(t.right.val) ?? 0) + 1);
        }
        let root: TreeNode | null = null;
        for (const t of trees) {
            if (!leafCount.has(t.val)) {
                root = t;
                break;
            }
        }
        if (!root) return null;
        const used = new Set<number>();
        function dfs(node: TreeNode): TreeNode {
            if (mp.has(node.val) && node !== root && !used.has(node.val)) {
                used.add(node.val);
                node = mp.get(node.val)!;
            }
            if (node.left) node.left = dfs(node.left);
            if (node.right) node.right = dfs(node.right);
            return node;
        }
        root = dfs(root);
        let total = 0;
        function valid(node: TreeNode | null, mn: number, mx: number): boolean {
            if (!node) return true;
            if (node.val <= mn || node.val >= mx) return false;
            total++;
            return valid(node.left, mn, node.val) && valid(node.right, node.val, mx);
        }
        if (!valid(root, -Infinity, Infinity) || total != trees.length * 3) return null;
        return root;
    }
}

Complexity

  • ⏰ Time complexity: O(n), since each tree and node is visited once.
  • 🧺 Space complexity: O(n), for hash maps and recursion stack.

Comments